96. Какими свойствами и параметрами характеризуются поверхности второго порядка?

Поверхности второго порядка типа в зависимости от значения коэффициентов могут описывать две плоскости, конусы, гиперболоиды параболоиды и эллипсоиды.

Поверхности второго порядка. Из аналитической геометрии известно, что функция вида

(2.2.1)

в зависимости от выбора коэффициентов может описывать поверхности эллипсоида, гиперболоида, конуса, параболоида, цилиндра или двух плоскостей. Все поверхности второго порядка, за исключением эллипсоида, не локализованы в пространстве и простираются в бесконечность. Поэтому только эллипсоид может самостоятельно образовывать объемный примитив, все другие квадратичные формы требуют пространственного ограничения линией или другими поверхностями.

Наиболее удобно с вычислительной точки зрения представлять квадратичную функцию (2.2.1) в матричном виде:

, (2.2.2)

где

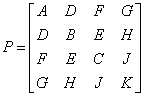. (2.2.3)

Нормальный вектор к квадратичной поверхности в точке определяется по правилу

, (2.2.4)

где

;

,

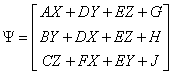а – орты осей . Направлен такой вектор по градиенту скалярного поля , т. е. в ту сторону, где наблюдается возрастание значений . Так как функция является монотонной и однократно знакопеременной, то нормаль направлена в ту часть подпространства, где значения функции положительны. Например, нормаль к поверхности шара, заданного уравнением , нацелена внутрь шара, а нормаль к поверхности того же шара, но заданного в виде , уже направлена наружу шара.

Часто используется операция пространственного переноса предварительно заданной квадратичной поверхности. Известны способы определения коэффициентов уравнения квадратичной поверхности (2.2.2) при изменении системы координат.

Если в системе координат квадратичная поверхность задается матрицей , а для перевода некоторой точки из этой системы в другую – необходимо применить преобразование :

,

где – матрица размера элемента, то новая матрица квадратичной поверхности в новой системе координат будет определяться по правилу

. (2.2.5.)

Значение функции в одной и той же точке пространства инвариантно к смене системы координат, в которой эта функция задана. Следовательно, ориентация нормали к поверхности при перемещении самой поверхности тоже инвариантна.

ПРИМЕРЫ Поверхностей второго порядка

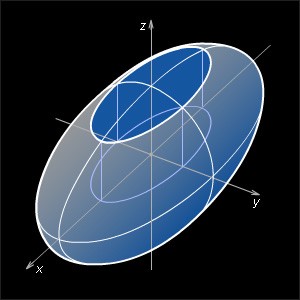
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением a > 0, b > 0, c > 0, называется эллипсоидом.

1

Свойства эллипсоида.

1. Эллипсоид – ограниченная поверхность.

2. Эллипсоид обладает

   • центральной симметрией относительно начала координат,

   • осевой симметрией относительно координатных осей,

   • плоскостной симметрией относительно начала координат.

3. В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением a > 0, b > 0, называется эллиптическим параболоидом.

Свойства эллиптического параболоида.

1. Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z ≥ 0 и принимает сколь угодно большие значения.

2. Эллиптический параболоид обладает

   • осевой симметрией относительно оси Oz ,

   • плоскостной симметрией относительно координатных осей Oxz и Oyz .

3. В сечении эллиптического параболоида плоскостью, ортогональной (перпендикулярной) оси Oz , получается эллипс, а плоскостями, ортогональными осям Ox и Oy – парабола.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением a > 0, b > 0, называется гиперболическим параболоидом.

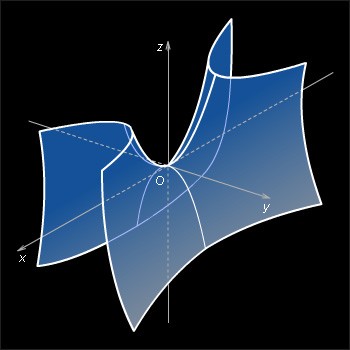
Свойства гиперболического параболоида.

1. Гиперболический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.

2. Гиперболический параболоид обладает

   • осевой симметрией относительно оси Oz ,

   • плоскостной симметрией относительно координатных плоскостей Oxz и Oyz .

3. В сечении гиперболического параболоида плоскостью, ортогональной оси координат Oz , получается гипербола, а плоскостями, ортогональными осям Ox и Oy , – парабола.

4. Гиперболический параболоид может быть получен поступательным перемещением в пространстве параболы так, что ее вершина перемещается вдоль другой параболы, ось которой параллельна оси первой параболы, а ветви направлены противоположно, причем их плоскости взаимно перпендикулярны.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением a > 0, b > 0, c > 0, называется однополостным гиперболоидом.

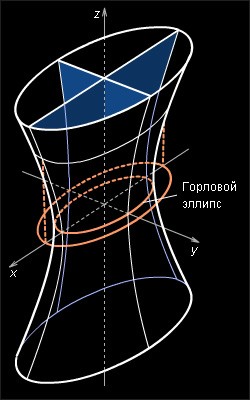
Свойства однополостного гиперболоида.

1. Однополостной гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.

2. Однополостной гиперболоид обладает

   • центральной симметрией относительно начала координат,

   • осевой симметрией относительно всех координатных осей,

   • плоскостной симметрией относительно всех координатных плоскостей.

3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz , получается эллипс, а плоскостями, ортогональными осям Ox и Oy – гипербола.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением a > 0, b > 0, c > 0, называется двуполостным гиперболоидом.

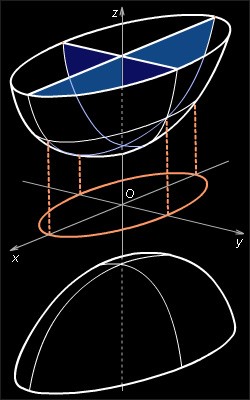
Свойства двуполостного гиперболоида.

1. Двуполостный гиперболоид – неограниченная поверхность,

2. Двуполостный гиперболоид обладает

   • центральной симметрией относительно начала координат,

   • осевой симметрией относительно всех координатных осей,

   • плоскостной симметрией относительно всех координатных плоскостей.

3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz , при |z|>c получается эллипс, при |z|=c – точка, а в сечении плоскостями, перпендикулярными осям Ox и Oy , – гипербола.