17. Определение дифференцируемости фнп. Необходимое условие дифференцируемости. Теорема о связи дифференцируемости фнп и существования частных производных.

Пусть функция 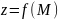определена в некоторой окрестности точки М.

Функция называется дифференцируемой функцией в точке М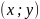 если её полное приращение в этой точке может быть представлено в виде:

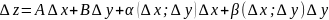
A,B – const, независящие от 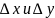; 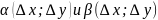– б.м. при

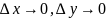
НЕОБХОДИМЫЕ УСЛОВИЯ дифференцируемости: Если дифференцируема в точке М , то она имеет в этой точке частные производные, при этом =A ;

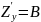
ДОКАЗАТЕЛЬСТВО. Т.к. дифференцируема в точке М , то . Пусть 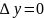, т.е. функция меняется только относительно переменной х, тогда её приращение будет иметь вид:

|

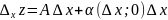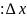
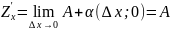. Аналогично

ТЕОРЕМА О СВЯЗИ ДИФ-СТИ ФНП и СУЩЕСТВОВАНИЯ ЧАСТН ПРОИЗВОДНОЙ. Если функция имеет частные производные в и эти производные непрерывно, то функция дифференцируема в точке М.

СЛЕДСТВИЕ. Из непрерывности частных производных следует непрерывность самой функции в этой точке.

18. Полный дифференциал функции двух переменных.

Если Z=f(M) дифференцируема в точке М (х;у), то её приращение может быть представлено в виде .

ОПРЕДЕЛЕНИЕ: (dz) дифференциалом дифференцируемой функции Z в точке М называется линейная относительно в x и у часть полного приращения функции в точке М, т.е. dZ=Ax+By.

В правой части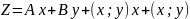 y третье и четвертое слагаемые являются бесконечно малыми функциями, по этому можно записать приближённое равенство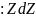 , что используется при приближённом вычислении.

Дифференциал второго порядка:

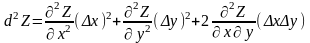
19. Производные сложной функции.

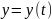Пусть функция такая, такая что и . Тогда 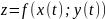называется сложной функцией. Где t – независимая переменная. y и x промежуточные переменные.

ТЕОРЕМА: Если функции и дифференцируемы в точке t , а функция дифференцируема в точке то сложная функция дифференцируема в точке t и справедлива формула:

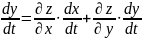
ДОКАЗАТЕЛЬСТВО. Придадим переменной t произвольное приращение , тогда x и y получат приращения , тогда 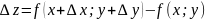. Т.к. функция z дифференцируема в точке то 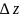можно записать в виде:

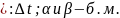
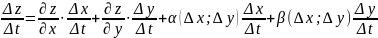
Перейдем к lim этого равенства при :

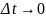lim =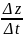

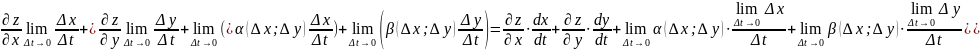
lim и lim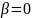 , т.к. по условию теоремы, функции x и y дифференцируемы в точке М следовательно они непрерывны в этой точке, а значит(согласно 2ому определению непрерывности функции в точке) пр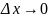и , и 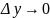следовательно

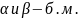
20. Определение производной по направлению.

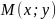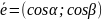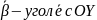Рассмотрим функцию , определенную в некоторой окрестности точки и рассмотрим произвольный единичный вектор , где , а , т.е. 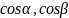-направляющие векторы. .

Для характеристики скорости изменения функции в точке М(x;y) в направлении 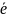введем понятие производной по направлению. Для этого проведем через т. М прямую L так чтобы одно из направлений на ней совпадало с направлением и возьмем на этой прямой точку

Обозначим длину 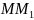через

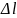
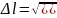
Тогда функция z получает приращение

Будем предполагать, что в окрестности т.М ф z непрерывна и имеет непрерывные частные производные(т.е. дифференцируемы). Тогда полное приращение ф.:

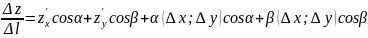
Перейдем к

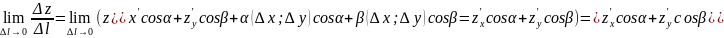
Если существует предел отношения т.е. 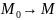, то он называется производной функции в точке по направлению вектора и обозначается:

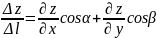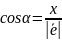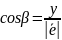; ; ; (x;y)

Или с помощью градиента: 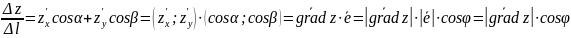где, 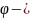угол между