
- •1. Определение монотонной функции. Необходимое и достаточное условие возрастания функции. Достаточное условие строгого возрастания функции.
- •2. Определение монотонной функции. Необходимое и достаточное условие убывания функции. Достаточное условие строгого убывания функции.
- •3. Определение локального экстремума функции одной переменной. Необходимое условие локального экстремума функции одной переменной.
- •4. Определение локального экстремума функции одной переменной. Первое достаточное условие строгого локального экстремума функции одной переменной.
- •5. Определение локального экстремума функции одной переменной. Второе достаточное условие строгого локального экстремума функции одной переменной.
- •6. Определение выпуклости и вогнутости функции одной переменной (выпуклость вверх, выпуклость вниз). Достаточное условие выпуклости функции одной переменной.
- •7. Определение точки перегиба графика функции одной переменной. Необходимое условие перегиба.
- •8. Определение точки перегиба графика функции одной переменной. Достаточное условие перегиба.
- •9. Определение вертикальной и наклонной асимптоты. Нахождение наклонной асимптоты.
- •10. Наибольшее и наименьшее значение функции одной переменной на замкнутом промежутке.
- •11. Формула Тейлора и формула Маклорена.
- •12. Разложение по формуле Маклорена функции , , .
- •13. Функции нескольких переменных (фнп). Основные определения. Предел фнп.
- •14. Непрерывность фнп. Основные свойства непрерывных функций.
- •15. Частные производные (определение, способы вычисления).
- •16. Частные производные старших порядков. Теорема о независимости смешанных производных от порядка дифференцирования.
- •17. Определение дифференцируемости фнп. Необходимое условие дифференцируемости. Теорема о связи дифференцируемости фнп и существования частных производных.
- •18. Полный дифференциал функции двух переменных.
- •19. Производные сложной функции.
- •20. Определение производной по направлению.
- •21. Определение градиента функции, линии уровня, свойства градиента.
- •22. Определение локального экстремума фнп. Необходимое условие экстремума фнп.
- •23. Определение локального экстремума фнп. Достаточное условие экстремума фнп.
- •24. Условный экстремум функции двух переменных (определение, метод подстановки и метод неопределенных множителей Лагранжа)
- •25. Наибольшее и наименьшее значение фнп в замкнутой и ограниченной области.
- •26. Определение первообразной функции. Теорема о свойствах первообразных функций.
- •27. Определение неопределенного интеграла. Теорема о существовании неопределенного интеграла (достаточное условие).
- •28. Таблица интегралов.
- •29. Свойства неопределенного интеграла.
- •30. Метод замены переменной (метод подстановки) в неопределенном интеграле.
- •31. Метод интегрирования по частям в неопределенном интеграле.
- •32. Определенный интеграл (определение, геометрический смысл).
- •33. Свойства определенного интеграла.
- •34. Интеграл с переменным верхним пределом. Теорема Барроу.
- •35. Формула Ньютона-Лейбница.
- •36. Метод замены переменной (метод подстановки) в определенном интеграле.
- •37. Метод интегрирования по частям в определенном интеграле.
- •38. Определение несобственного интеграла первого рода (по бесконечному промежутку).
- •39. Определение несобственного интеграла второго рода (от функций, имеющих разрыв).
- •40. Понятие о дифференциальных уравнениях. Общее и частное решение. Начальные условия. Задачи Коши.
- •41. Дифференциальные уравнения с разделяющимися переменными и метод их решения.
- •42. Однородные дифференциальные уравнения.
- •43. Линейные уравнения I-порядка.
1. Определение монотонной функции. Необходимое и достаточное условие возрастания функции. Достаточное условие строгого возрастания функции.
Функция называется монотонной на (a;b) если она возрастает или убывает на этом промежутке.
НЕОБХОДИМОЕ УСЛОВИЕ возрастания/убывания функции.
Если
дифференцируемая на
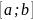 функция
f(x)
возрастает/убывает, то
функция
f(x)
возрастает/убывает, то
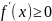 /
f’(x)
/
f’(x)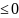 .
.
ДОКАЗАТЕЛЬСТВО.
Пусть
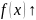 на
.
Возьмем произвольную точку
на
.
Возьмем произвольную точку
 и
и
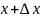 (
(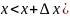 .
.
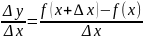
1)
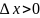 ;
;
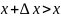 ;
;
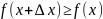 ;
;
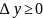 ;
;
 .
.
2)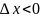 ;
;
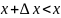 ;
;
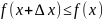 ;
;
 ;
.
;
.
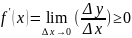
ГЕОМЕТРИЧЕСКИ это означает, что касательная к графику возрастающей/убывающей функции образует острые/тупые углы с положительным направление OX и в некоторых точках || OX.
ДОСТАТОЧНОЕ УСЛОВИЕ возрастания функции.
Если функция дифференцируема на (a;b) и
 на
,
то функция возрастает на данном
промежутке.
на
,
то функция возрастает на данном
промежутке.Если функция
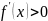 ,
то функция строго возрастает убывает.
,
то функция строго возрастает убывает.
ДОКАЗАТЕЛЬСТВО.
Пусть
,
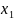 и
и
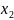 - произвольные точки на
,
такие что
- произвольные точки на
,
такие что
 , тогда на
, тогда на
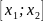 выполнены все условия теоремы Лагранжа.
выполнены все условия теоремы Лагранжа.
 ,
где
,
где
 ;
;
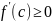 ,
,

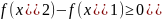 ,
т.е.
,
т.е.
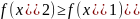 ,
а следовательно функция возрастает.
,
а следовательно функция возрастает.
2. Определение монотонной функции. Необходимое и достаточное условие убывания функции. Достаточное условие строгого убывания функции.
Функция называется монотонной на (a;b) если она возрастает или убывает на этом промежутке.
НЕОБХОДИМОЕ УСЛОВИЕ возрастания/убывания функции.
Если
дифференцируемая на
функция
 убывает,
то f’(x)
.
убывает,
то f’(x)
.
ДОКАЗАТЕЛЬСТВО.
Пусть
 на
Возьмем
произвольную точку
и
(
на
Возьмем
произвольную точку
и
(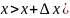 .
.
1) ; ; ; ; .
2) ; ; ; ; .
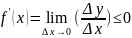
ГЕОМЕТРИЧЕСКИ это означает, что касательная к графику возрастающей/убывающей функции образует острые/тупые углы с положительным направление OX и в некоторых точках || OX.
ДОСТАТОЧНОЕ УСЛОВИЕ возрастания/убывания функции.
Если функция дифференцируема на (a;b) и
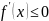 на
,
то функция возрастает/убывает данном
промежутке.
на
,
то функция возрастает/убывает данном
промежутке.Если функция
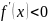 , то функция строго убывает.
, то функция строго убывает.
ДОКАЗАТЕЛЬСТВО. Пусть , и - произвольные точки на , такие что , тогда на выполнены все условия теоремы Лагранжа.
,
где
;
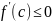 ,
,
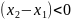
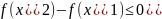 ,
т.е.
,
т.е.
 ,
а следовательно функция убывает.
,
а следовательно функция убывает.
3. Определение локального экстремума функции одной переменной. Необходимое условие локального экстремума функции одной переменной.
Точка
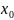 является точкой локального max/min
функции
,
если для любого x
из
является точкой локального max/min
функции
,
если для любого x
из
 -окрестности
точки
выполняется: 1)
-окрестности
точки
выполняется: 1)
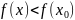 для max
для max
2)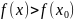 для min
для min
Понятие экстремума всегда связано с определенной окрестностью точки из ООФ. Поэтому функция имеет экстремум только во внутренних точках ООФ.
НЕОБХОДИМОЕ
УСЛОВИЕ ЛОКАЛЬНОГО ЭКСТРЕМУМА. Если
имеет в точке
локальный экстремум и дифференцируема
в этой точке, то
 .
.
ДОКАЗАТЕЛЬСТВО.
Т.к. в точке
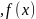 имеет локальный экстремум, то по
определению экстремума существует
такая
-окрестность
точки
, в которой значение
имеет локальный экстремум, то по
определению экстремума существует
такая
-окрестность
точки
, в которой значение
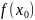 является наибольшим или наименьшим
среди всех значений функции на этом
интервале. Тогда по теореме Ферма
.
является наибольшим или наименьшим
среди всех значений функции на этом
интервале. Тогда по теореме Ферма
.
ГЕОМЕТРИЧЕСКИ значит, что в точке экстремума дифференцируемой функции касательная к её графику || OX.
Такие
точки экстремума являются точками
ГЛАДКОГО ЭКСТРЕМУМА; если в точке
экстремума
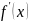 не существует – это точка УЗКОГО
ЭКСТРЕМУМА (например, график
не существует – это точка УЗКОГО
ЭКСТРЕМУМА (например, график
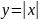 ).
).
ОБРАТНАЯ
ТЕОРЕМА НЕ ВЕРНА. Т.е. если
,
 .
.
Таким образом непрерывная функция может иметь экстремум лишь в точках в которых или не существует. Такие точки называются стационарными/критическими/ подозрительными на экстремум.
