Дифференциальные уравнения, допускающие понижение порядка.

В этой статье рассмотрим дифференциальные уравнения порядка выше второго, в которых есть возможность понижения порядка с помощью замены. Среди таких уравнений наиболее часто встречаются ОДУ  , которые не содержат искомой функции и производных до k – 1 порядка, и дифференциальные уравнения вида  , которые не содержат независимого переменного.Порядок дифференциального уравнения   может быть снижен до n – k заменой переменных  . При такой замене получим  . После подстановки этих результатов в исходное уравнение получим дифференциальное уравнение порядка n – k с неизвестной функцией p(x). После нахождения p(x), функция y(x) может быть найдена из равенства  интегрированием k раз подряд.

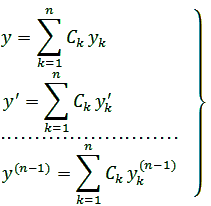
Билет 20

Уравнение вида y''+ρy'+qy=f(x), где ρ и q – вещественные числа, f(x) – непрерывная функция, называется линейным дифференциальным уравнением с постоянными коэффициентами. Рассмотрим линейное уравнение второго порядка вида: y''+ρy'+qy=0, (1) у которого правая часть f(x) равна нулю. Такое уравнение называется однородным. Уравнение K²+ρK+q=0 (2) называется характеристическим уравнением данного уравнения (1). Характеристическое уравнение (2) является квадратным уравнением, имеющим два корня. Обозначим их через К₁ и К₂. Общее решение уравнения (1) может быть записано в зависимости от величины дискриминантаD=ρ²–4q уравнения (2) следующим образом:

1. При D>0 корни характеристического уравнения вещественные и различные (К₁≠К₂), и общее решение имеет вид  .

2. При D=0 корни характеристического уравнения вещественные и равные (К₁=К₂=К), и общее решение имеет вид:  3. Если D<0, то корни характеристического уравнения комплексные:  , где   – мнимая единица,   и общее решение (К₁=α+βi, К₂=α–βi, β≠0), имеет вид y=e^αx(C₁ cosβx+C₂ sinβx).

Решением дифференциального уравнения называется всякая функция y = φ (x), которая при подстановке в уравнение обращает его в верное равенство.

График решения дифференциального уравнения называется интегральной кривой этого уравнения. Процесс нахождения решения дифференциального уравнения называется интегрированием этого уравнения.

Не всегда удается получать решения в явном виде, например

x2 + y2 = C.

Решение дифференциального уравнения, полученное в неявном виде F (x, y) = 0, называется интегралом дифференциального уравнения.

Общим решением дифференциального уравнения называется такое его решение, содержащее произвольные постоянные, из которого любое частное решение может быть получено при соответствующем подборе произвольных постоянных.

Построение общего решения однородного линейного уравнения по фундаментальной системе решений

Знание фундаментальной системы решений уравнения L(y) = 0 дает возможность построить общее решение этого уравнения.

Основная теорема. Если функции(11.3)образуют фундаментальную систему решений однородного линейного уравнения n-го порядка L(y) в интервале (a,b), т. е. в интервале непрерывности коэффициентов p₁(x), …, p_n(x), то функция (11.1) дает общее решение этого уравнения в области

a<x<b, |y| < + ∞, |y| < + ∞, …, |y^{(n – 1)}| < + ∞.(11.5)

   В самом деле, в каждой точке области (11.5) имеет место существование и единственность решения задачи Коши. Покажем, что функция (11.1) удовлетворяет обоим условиям, указанным в определении общего решения уравнения n-го порядка.

   1. Система уравнений

(11.6)

разрешима в области (11.5) относительно произвольных постоянных C₁, C₂, …, C_n так как определитель этой системы, будучи равен определителю Вронского для фундаментальной системы решений (11.3), отличен от нуля.

   2. Функция (11.1) по третьему свойству решений однородного линейного уравнения является решением уравнения L(y) = 0 при всех значениях произвольных постоянных C₁, C₂, …, C_n.

   Поэтому функция (11.1) является общим решением уравнения L(y) = 0 в области (11.5).

   Формула (11.1) содержит в себе все решения уравнения L(y) = 0, ибо она дает возможность найти решение, удовлетворяющее начальным условиям

y = y₀, y ' =  , …, y ^{(n – 1)} =   при x = x₀       (11.7)

где y₀,  , …,   можно задавать произвольно, а x₀ брать любым из интервала (a, b). Для этого достаточно подставить в систему (11.6) вместо x, y, y ', …, y^{(n – 1)} начальные данные x₀, y₀,  , …,   и разрешить полученную систему

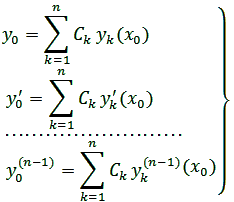( 11.8)

относительно произвольных постоянных C₁, C₂, …, C_n. Так как определитель системы (11.8) есть W(x₀) и он отличен от нуля вследствие того, что система решений (11.3) фундаментальная, то эта система имеет единственное решение

C₁ =  , C₂ =  , …, C_n =  Подставляя найденные значения произвольных постоянных в общее решение (11.1), получим искомое решение:y =     y_k.Таким образом, фундаментальная система решений (11.3) является базисом n–мерного линейного пространства решений уравнения L(y) = 0.