Билет 9

Формула Ньютона – Лейбница

Пусть функция у = f(x) интегрируема на отрезке [а; b]. Если функция у = f(x) непрерывна на отрезке [а; b] и F(x) – какая-либо её первообразная на [a; b] (F'(x) = f(x)), то имеет место формула =F(b)-F(a) (4) Равенство (4) называется формулой Ньютона - Лейбница. Если ввести обозначение F(b) - F(a) = F(x) , то формулу Ньютона-Лейбница (4) можно переписать так: 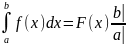Формула Ньютона – Лейбница даёт удобный способ вычисления определённого интеграла.Чтобы вычислить определенный интеграл от непрерывной функции f(x) на отрезке [а; b], надо найти её первообразную функцию F(x) и взять разность F(b) - F(a) значений этой первообразной на концах отрезка [а; b].

Билет 8

Геометрический смысл

Площадь криволинейной трапеции

Пусть на отрезке [а; b] задана непрерывная функция у = f(x)≥0. Фигура, ограниченная сверху графиком функции у = f(х), снизу – осью Ох, сбоку – прямыми х = а и х = b, называется криволинейной трапецией. Найдем площадь этой трапеции. Для этого отрезок [а; b] точками а = x₀, x₁, …, b = x_n (x₀ < x₁ < … < x_n) разобьем на n частичных отрезков [x₀; x₁], [x₁;x₂], …, [x_n-1; x_n] (рис. 2.). В каждом частичном отрезке [x_i-1; x_i], (I = 1, 2, …, n) возьмем произвольную точку и вычислим значение функции в ней, т. е. f(c_i).Умножим значением функции f(c_i) на длину Δx_i = x_i - x_i-1 соответствующего частичного отрезка. Произведение f(c_i) ⋅ Δx_i равно площади прямоугольника с основанием Δx_i и высотой f(c_i). Сумма всех таких произведений f(c₁) Δx₁ + f(c₂) Δx₂ + … + f(c_n) Δx_n = 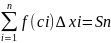равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции: S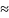 S_n= С уменьшением всех величин Δx_i точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры S_n, когда n неограниченно возрастает так, что λ = max Δx_i → 0: S=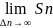 = 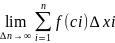тоесть S= Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.В этом состоит геометрический смысл определенного интеграла.

Билет 11

Дифференциальное исчисление функций нескольких переменных

Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести понятие функции нескольких переменных. Будем рассматривать функции двух переменных, так как все важнейшие факты теории функций нескольких переменных наблюдаются уже на функциях двух переменных. Эти факты обобщаются на случай большего числа переменных. Кроме того, для функций двух переменных можно дать наглядную геометрическую интерпретацию

1°. Понятие функции нескольких переменных. Функциональные обозначения.Пусть задано множество D упорядоченных пар чисел (х;у). Соответствие f, которое каждой паре чисел (x; у) ∈ D сопоставляет одно и только одно число z∈R, называется функцией двух переменных, определенной на множестве D со значениями в R, и записывается в виде z =f(х; у) или f : D→R. При этом х и у называются независимыми переменными (аргументами), а z — зависимой переменной (функцией).

А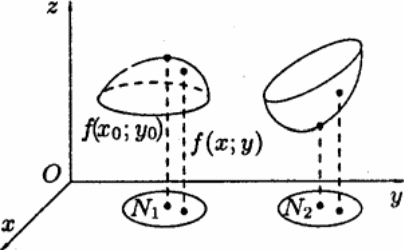 налогично определяются функции трех и большего числа аргументов. Множество D=D(f) называется областью определения функции. Множество значений, принимаемых z в области определения, называется областью изменения этой функции, обозначается Е(f) или Е.

Функцию z = f(х;у), где (х;у) ∈ D можно понимать (рассматривать) как функцию точки

М(х;у) координатной плоскости Оху. Значение функции z=f(x; у) в точке Мо(хо;yо) обозначают

z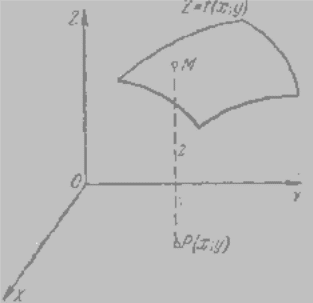 _о = f(x_оy_о) или z_о = f(М_о) и называют частным значением функции. Функция двух независимых переменных допускает геометрическое истолкование. Каждой точке Мо(x_о; y_о) области D в системе координат Охуz соответствует точка М(х_о; у_о; z_о), где z_о=f(х_о;у_о) — аппликата точки М. Значение функции г=f(х, y) в точке Р(a; b), т.е. при х = а и у = b,обозначается f(а, b) или f(Р). Геометрическим изображением функции z=f(х, у) в прямоугольной системе координат X, У, Z, вообще говоря, является некоторая поверхность

Функция двух переменных, как и функция одной переменной, может быть задана разными способами: таблицей, аналитически, графиком. Будем пользоваться, как правило, аналитическим способом: когда функция задается с помощью формулы. Примером функции двух переменных может служить площадь S прямоугольника со сторонами, длины которых равны х и у: S == ху. Областью определения этой функции является множество {(х; у) | х > 0, у > О}.

П р и м е р . Выразить объем конуса V как функцию его образующей х и радиуса основания у.

Решение. Из геометрии известно, что объем конуса равен ,V = 1/3πy^2h где h — высота конуса. Но h = x2 − y2 . Следовательно, V = 1/3πy^2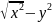 Это и есть искомая функциональная зависимость.