Билет 21 Линейные дифференциальные уравнения второго порядка.

В этой статье рассмотрим основные принципы нахождения общего решения линейных однородных и неоднородных дифференциальных уравнений второго порядка, и подробно разберем решения нескольких примеров. Линейное однородное дифференциальное уравнение второго порядка имеет вид  , а неоднородное  , где функции f(x), p(x) и q(x) - непрерывны на интервале интегрирования X. В частном случае, когда функции p(x) = p и q(x) = q есть постоянные,

Общим решением y₀ линейного однородного дифференциального уравнения  на интервале X с непрерывными коэффициентами   на X является линейная комбинация n линейно независимых частных решений ЛОДУ   с произвольными постоянными коэффициентами  , то есть  .Общее решение y линейного неоднородного дифференциального уравнения   на интервале X с непрерывными на том же промежутке Xкоэффициентами   и функцией f(x) представляет собой сумму  , где y₀ - общее решение соответствующего ЛОДУ  , а   - какое-нибудь частное решение исходного ЛНДУ.Таким образом, y₀ = C₁ ⋅ y₁ + C₂ ⋅ y₂ - общее решение дифференциального уравнения  , где y₁ и y₂ – его линейно независимые частные решения,а   - общее решение уравнения  , где   - любое из его частных решений, а y₀ - общее решение соответствующего ЛОДУ.Осталось научиться находить y₁, y₂ и  . В самых простых случаях эти функции подбираются.Линейно независимые функции y₁ и y₂ наиболее часто находятся среди наборов

 

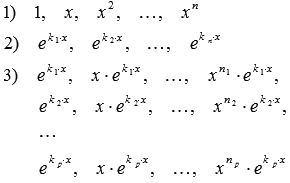
Л инейная независимость функций y₁ и y₂ проверяется с помощью определителя Вронского  . Если функции линейно независимы на интервале X, то определитель Вронского отличен от нуля для любого x из промежутка X.К примеру, функции y₁ = 1 и y₂ = x линейно независимы для любого действительного значения x, так как .Функции y₁ = sinx и y₂ = cosx также линейно независимы на R, так как  А вот функции y₁ = - x - 1 и y₂ = x + 1 линейно зависимы на интервале (-∞; +∞), так как В общем случае подбор y₁, y₂ и   труден и далеко не всегда возможен. Если получится подобрать нетривиальное частное решение y₁ ЛОДУ второго порядка  , то его общее решение можно отыскать, понизив степень уравнения до первой с помощью подстановки  .

Билет 22

3.12. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.

 Характеристическое уравнение линейного дифференциального уравнения

Рассмотрим линейное уравнение n-го порядка

L(y) ≡ y ⁽ⁿ⁾ + a₁ y ^{(n – 1)} + … + a_{n – 1} y ' + a_n y = f (x),       (12.1)

где коэффициенты a₁, a₂, …, a_n суть действительные числа, а правая часть f (x) непрерывна в некотором интервале (a, b) (a ≥ – ∞, b ≤ + ∞).Так как интегрирование неоднородного линейного уравнения приводится к интегрированию соответствующего однородного уравнения, то рассмотрим сначала вопрос о построении общего решения однородного уравнения L(y) ≡ y ⁽ⁿ⁾ + a₁ y ^{(n – 1)} + … + a_{n – 1} y ' + a_n y = 0.       (12.2)

Для нахождения общего решения этого уравнения достаточно знать фундаментальную систему решений. Так как коэффициенты уравнения постоянны и, следовательно, заведомо непрерывны при всех значениях x, то согласно теореме Пикара и все решения уравнения (12.2) определены при всех значениях x. Поэтому в дальнейшем мы не будем указывать ни интервал существования частных решений, ни область задания общего решения.

   Эйлер доказал, что для однородного линейного уравнения с постоянными коэффициентами всегда можно построить фундаментальную систему решений, состоящую из элементарных функций, и, следовательно, это уравнение всегда интегрируется в элементарных функциях. Ниже это утверждение доказывается для уравнения второго порядка и распространяется на уравнение n-го порядка.

   Рассмотрим уравнение второго порядка

L(y) ≡ y '' + py ' + qy = 0,       (12.3)

где p и q — действительные числа. Будем, следуя Эйлеру, искать частное решение уравнения (12.3) в виде

y=e^λx, (12.4)

где λ — подлежащее определению число (действительное или комплексное). Согласно определению решения функция (12.4) будет решением уравнения (12.3), если λ выбрано так, что функция (12.4) обращает это уравнение в тождество

L(e^λx) ≡ 0. (12.5)

Вычисляя L(e^λx), т. е. подставляя функцию (12.4) в левую часть уравнения (12.3), и принимая во внимание, что

            (e^λx)^(k) = λ^k e^λx,       (12.6)

будем иметьL(e^λx) = (e^λx)'' + p(e^λx)' + q(e^λx) = (λ² + pλ + q)e^λx,

так чтоL(e^λx) = (λ² + pλ + q)e^λx(12.7)или

L(e^λx) = P(λ)e^λx,гдеP(λ) =λ²+pλ+q.Из формулы(12.7)следует, что интересующее нас тождество (12.5) будет выполняться тогда и только тогда, когда P(λ) = 0, т. е. когда λ является корнем уравнения

            λ² + pλ + q = 0.       (12.8)   Это уравнение называется характеристическим уравнением, а его корни — характеристическими числами уравнения (12.3).   Заметим, что характеристическое уравнение (12.8) может быть составлено по данному дифференциальному уравнению (12.3) заменой y '', y ' и y на λ², λ и 1, т. е. степень λ совпадает с порядком производной, если условиться считать, что производная нулевого порядка от функции есть сама функция y⁽⁰⁾ ≡ y.   Структура фундаментальной системы решений, а вместе с ней и общего решения уравнения (12.3) зависит от вида корней характеристического уравнения(12.8). 

Билет 23+24

Линейное неоднородное дифференциальное уравнение (ЛНДУ) второго порядка с постоянными коэффициентами имеет вид  , где p и q – произвольные действительные числа, а функция f(x) – непрерывна на интервале интегрирования X.Сформулируем теорему, которая показывает в каком виде искать общее решение ЛНДУ. Общее решение на интервале X линейного неоднородного дифференциального уравнения   с непрерывными на интервале интегрирования X коэффициентами   и непрерывной функцией f(x) равно сумме общего решения   соответствующего ЛОДУ и какого-нибудь частного решения   исходного неоднородного уравнения. То есть,  .Таким образом, общим решением линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами является сумма  . Существует несколько методов нахождения частного решения ЛНДУ второго порядка с постоянными коэффициентами. Методы выбираются в зависимости от вида функции f(x), стоящей с правой части уравнения.

Если f(x) является многочленом n-ой степени f(x) = P_n(x), то частное решение ЛНДУ ищется в виде  , где Q_n(x) – многочлен степени n, а r – количество корней характеристического уравнения, равных нулю. Так как   - частное решение уравнения  , то коэффициенты, определяющие многочлен Q_n(x), находятся методом неопределенных коэффициентов из равенства  .

Решение задачи Коши для неоднородного дифференциального уравнения с постоянными коэффициентами можно найти методом вариации произвольных постоянных (методом Лагранжа), который состоит в следующем:  Записываем искомое решение задачи Коши для неоднородного уравнения  в виде  y(x)= c₁(x) y₁(x) +  c₂(x) y₂(x) + ... + c_n(x) y_n(x),где  y₁(x),  y₂(x), ..., y_n(x)  — линейно независимые решения соответствующего однородного уравнения, и находим неизвестные функции c₁(x) ,  c₂(x), ...,  c_n(x),такие, чтобы функция y = y(x) удовлетворяла неоднородному уравнению и заданным начальным условиям.

Опишем алгоритм решения задачи Коши для уравнения второго порядка y'' + a₁ y' + a₂ y = f(x), y(x₀)=y₀, (y)'(x₀)=y_0,1. Будем искать решение задачи в видеy(x)= c₁(x) y₁(x) +  c₂(x) y₂(x), где  y₁(x),  y₂(x) — линейно независимые решения однородного уравненияy'' + a₁ y' + a₂ y = 0.Вычислим  y'(x), y''(x)  и подставим полученные выражения в уравнение. Вычислим первую производнуюy'(x)= (c₁'(x) y₁(x) +  c₂(x)' y₂(x)) + (c₁(x) y₁'(x) +  c₂(x) y₂'(x)), положим c₁'(x) y₁(x) +  c₂(x)' y₂(x)  = 0и тогда y'(x)= c₁(x) y₁'(x) +  c₂(x) y₂'(x),y''(x)= (y'(x))'= (c₁(x) y₁'(x) +  c₂(x) y₂'(x))'==c₁'(x) y₁'(x) +  c₂(x)' y₂'(x) + c₁(x) y₁''(x) +  c₂(x) y₂''(x).Подставив y(x) и ее производные в уравнение, получим: y'' + a₁ y' + a₂ y == c₁'(x) y₁'(x) +  c₂(x)' y₂'(x) + c₁(x) y₁''(x) +  c₂(x) y₂''(x) + + a₁(c₁(x) y₁'(x)+c₂(x) y₂'(x)) + a₂(c₁(x) y₁(x)+c₂(x) y₂(x)) = c₁(x)( y₁''(x)+a₁ y₁'(x)+a₂ y₁(x)) + c₂(x)( y₂''(x)+a₁ y₂'(x)+a₂ y₂(x)) + c₁'(x) y₁'(x) +  c₂(x)' y₂'(x) = 0 + 0 + c₁'(x) y₁'(x) +  c₂(x)' y₂'(x) = f(x),при условии c₁'(x) y₁(x) +  c₂(x)' y₂(x)  = 0.Тогда неизвестные функции c₁(x) и c₂(x) являются решениями системы линейных дифференциальных уравнений c₁'(x) y₁'(x) +  c₂(x)' y₂'(x) =  f(x),c₁'(x) y₁(x) +  c₂(x)' y₂(x)  = 0с известными y₁(x) и y₂(x).Эта система легко разрешима относительно c₁(x) и c₂(x):c₁'(x) =  f(x)y₂(x)/(y₁'(x)y₂(x)-y₁(x)y₂'(x)), c₁'(x)= f(x)y₁(x)/(y₁(x)y₂'(x)-y₁'(x)y₂(x)).Вычислив интегралы в правой части системы, получим

Произвольные константы C₁  и  C₂   определяются из начальных условий.