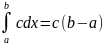Билет 3

Первообразная функция

Определение: Функция F(x) называется первообразной функцией функции f(x) на отрезке

[a, b], если в любой точке этого отрезка верно равенство: F′(x) = f(x).Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число. F₁(x) = F₂(x) + C.

Неопределенный интеграл и его непосредственное вычисление Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением: F(x) + C. Записывают: ∫f(x)dx=F(x)+C;

Условием существования неопределенного интеграла на некотором отрезке является

непрерывность функции на этом отрезке.

Билет 4

Свойства неопределенного интеграла.

1.∫( f (x)dx)’ =(F(x) + C)′ = f (x);

2.d(∫ f (x)dx)= f (x)dx;

3.∫ dF(x) = F(x) + C;

4.∫(u + v − w)dx = ∫udx + ∫vdx − ∫ wdx; где u, v, w – некоторые функции от х.

5.∫C ⋅ f (x)dx = C ⋅ ∫ f (x)dx;

Билет 6=10

Способ подстановки

Теорема: Если требуется найти интеграл ∫f(x)dx , но сложно отыскать первообразную, то с

помощью замены x = ϕ(t) и dx = ϕ′(t)dt получается:

∫ f (x)dx = ∫ f (ϕ(t))ϕ′(t)dt

Доказательство: Продифференцируем предлагаемое равенство:

d ∫ f (x)dx = d(∫ f [ϕ(t)]ϕ′(t)dt) По рассмотренному выше свойству №2 неопределенного интеграла: f(x)dx = f[ϕ(t)]ϕ′(t)dt что с учетом введенных обозначений и является исходным предположением. Теорема доказана.

Интегрирование по частям

Способ основан на известной формуле производной произведения:

(uv)′ = u′v + v′u, где u и v – некоторые функции от х.

В дифференциальной форме: d(uv) = udv + vdu

Проинтегрировав, получаем: ∫ d(uv) = ∫udv + ∫vdu , а в соответствии с приведенными выше

свойствами неопределенного интеграла: uv = ∫udv + ∫vdu или ∫udv = uv − ∫vdu ;

Получили формулу интегрирования по частям, которая позволяет находить интегралы

многих элементарных функций.

Билет 7

Определенный интеграл как предел интегральной суммой

Пусть функция у = f(x) определена на отрезке [a; b], a < b. Выполним следующие действия.

С помощью точек x₀ = a, x₁, x₂, …, x_n = b (x₀<x₁< … <x_n) разобьем отрезок [а, b] на п

частичных отрезков [x₀; x₁], [x₁; x₂], …, [x_n-1; x_n]

c₁ c₂ c_i c_n x

О x₀ = a, x₁, x_i-1 x_{i b} = x_n

В каждом частичном отрезке [x_i-1; x_i], i = 1, 2, …, n выберем произвольную точку ci ∈ [x_i-1; x_i],

и вычислим значение функции в ней, т.е. величину f(c_i).Умножим найденное значение функции f(ci) на длину Δx_i = x_i - x_i-1 соответствующего частичного отрезка: f(c_i) ⋅ Δx_i.Составим сумму Sn всех таких произведений:S_n = f(c₁) Δx₁ + f(c₂) Δx₂ + … + f(c_n) Δx_n =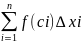 Сумма вида (1) называется интегральной суммой функции у = f(x) на отрезке [а; b].Обозначим через λ длину наибольшего частичного отрезка: λ = max Δx_i (i = 1, 2, …n).5. Найдем предел интегральной суммы, когда n → ∞ так, что λ → 0. 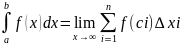Если при этом интегральная сумма Sn имеет предел I, который не зависит ни от способа разбиения отрезка [а; b] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции у = f(x) на отрезке [а; b] и обозначается Таким образом, Числа а и b называются соответственно нижним и верхним пределами интегрирования, f(x) –подынтегральной функцией, f(x) dx – подынтегральным выражением, х – переменной нтегрирования, отрезок [а; b] – областью (отрезком) интегрирования. Функция у = f(x), для которой на отрезке [а; b] существует определенный интеграл называется интегрируемой на этом отрезке. Если функция у= f(x) непрерывна на отрезке [а; b], то определенный существует.Непрерывность функции является достаточным условием ее интегрируемости. Однако определенный интеграл может существовать и для некоторых разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва.

Укажем некоторые свойства определенного интеграла, непосредственно вытекающие из его

определения (2).

1. Определенный интеграл не зависит от обозначения переменной интегрирования:

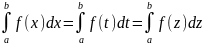
Это следует из того, что интегральная сумма (1), а, следовательно, и ее предел (2) не зависят

от того, какой буквой обозначается аргумент данной функции.

2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:

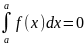
3. Для любого действительного числа