
- •1.Метод и законы термодинамики. Основные понятия и определения термодинамики.
- •2.Параметры состояния и уравнения состояния.
- •3.Термодинамическая работа. Координаты р-V.
- •4. Потенциальная работа. Координаты р-V. Распределение работы.
- •5. Истинная и средняя теплоемкости веществ.
- •6.Смеси жидкостей, паров и газов, расчет характеристик смеси веществ.
- •7. Схемы смешения. Закон Дальтона.
- •8. Определение температуры смеси. Теплоемкость смеси.
- •9. Термодинамические условия фазовых переходов
- •10. Критические параметры чистого вещества и смесей газов.
- •11. Теория соответственных состояний. Коэффициент сжимаемости.
- •12. Постулат и математическое выражение 1 начала термодинамики.
- •13. Первое начало термодинамики в аналитическое форме.
- •14. 1 Начало термодинамики для идеального газа.
- •15. Принцип существования энтропии идеального газа.
- •1 6. Изобарный процесс изменения состояния простого тела. Уравнение процесса, изображение в координатах p-V, связь между параметрами, работа и теплообмен, изменение функций состояния.
- •17. Изобарный процесс изменения состояния идеального газа. Уравнение процесса, изображение в координатах t-s, связь между параметрами, работа и теплообмен, изменение функций состояния.
- •18. Изохорный процесс изменения состояния простого тела. Уравнение процесса, изображение в координатах р-V, связь между параметрами, работа и теплообмен, изменение функций состояния.
- •19. Изохорный процесс изменения состояния идеального газа. Уравнения процесса, изображение в координатах t-s, связь между параметрами, работа и теплообмен, изменение функции состояния.
- •20. Изопотенциальный процесс изменения состояния простого тела. Уравнение процесса, изображение в координатах р-V, связь между параметрами, работа и теплообмен, изменение функций состояния.
- •31. Теплопроводность. Закон Фурье. Коэффициент теплопроводности.
- •32. Ду теплопроводности. Условия однозначности.
- •33. Теплопроводность через однослойные и многослойные плоские стенки.
- •34. Теплопроводность через однослойные и многослойные цилиндрические стенки.
- •35. Теплоотдача. Уравнение Ньютона. Коэффициент теплоотдачи.
- •36. Критериальные уравнения, физический смысл критериев подобия.
- •37. Последовательность расчетов конвективного теплообмена в в условиях свободной конвекции.
- •38. Последовательность расчетов конвективного теплообмена в условиях вынужденной конвекции.
- •39. Теплообмен излучением. Основные законы.
- •40. Теплообмен излучением между телами.
- •41. Коэффициент лучистого теплообмена. Уравнение Ньютона-Рихмана.
- •42. Сложный теплообмен. Эффективный коэффициент теплопроводности.
- •43. Теплопередача. Основное уравнение теплопередачи. Коэффициент теплопередачи.
- •44. Теплопередача через плоские однослойные и многослойные стенки.
- •45. Теплопередача через криволинейные однослойные и многослойные стенки.
- •46,(47).Оптимизация процессов теплопередачи. Способы интенсификации теплопередачи(Методы снижения теплового потока).
- •48. Теплопередача при переменных температурах. Средняя разность температур.
- •49. Тепловой баланс и уравнение теплопередачи теплообменного аппарата.
- •50. Средняя разность температур для сложных схем теплообмена.
- •51. Обобщенные уравнения теплопередачи при переменных температурах.
- •52. Последовательность расчета теплообменных аппаратов 1 рода.
- •53. Последовательность расчетов теплообменного аппарата 2 рода
- •54. Круговые процессы, кпд и холодильный коэффициент
- •55. Обратимый цикл Карно, прямой и обратный процесс. Теорема Карно.
- •56. Математическое выражение второго начала термостатики. Основные следствия.
- •57. Математическое выражение второго начала термодинамики. Основные следствия.
- •58. Истечение жидкостей и газов. Основные расчетные соотношения. Истечение несжимаемой жидкости.
- •59.Особенности истечения сжимаемой жидкости. Кризис истечения. Режимы истечения.
- •60. Переход через критическую скорость. Сопло Лаваля, определение геометрических размеров.
- •61. Особенности истечения через каналы переменного сечения, сопло и диффузор.
- •62. Дросселирование. Эффект Джоуля-Томсона. Основные понятия
- •63. Процессы парообразования, определение параметров насушенного пара, диаграмма h-s.
- •64.Классификация циклов тепловых двигателей:
- •65. Схема, рабочий процесс и тд цикл Брайтона. Кпд.
- •66. Схема, рабочий процесс и тд цикл Гемфри. Кпд.
- •67. Сопоставление тд циклов Брайтона и Гемфри по эффективности.
- •68. Схема, рабочий процесс и тд цикл Отто, кпд.
- •69. Схема, рабочий процесс и тд цикл Дизеля. Кпд
- •71. Сопоставление тд циклов двс по эффективности.
- •72. Схема, рабочий процесс и цикл паросиловой установки, цикл Ренкина, методы повышения кпд
- •73.Схема, рабочий процесс и цикл паросиловой установки с промежуточным перегревом
- •74. Схема, рабочий процесс и цикл паросиловой установки с регенерацией.
- •75. Схема, рабочий процесс и цикл паровой компрессионной холодильной машины.
- •77,78. Рабочий процесс двухтактного(и четырехтактного) двигателя внутреннего сгорания.
- •79. Индикаторные и эффективные характеристики двигателей внутреннего сгорания.
17. Изобарный процесс изменения состояния идеального газа. Уравнение процесса, изображение в координатах t-s, связь между параметрами, работа и теплообмен, изменение функций состояния.
Для идеального газа:
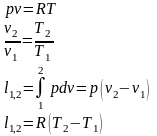
Первое начало термодинамики: .
Для идеального газа: и , .
18. Изохорный процесс изменения состояния простого тела. Уравнение процесса, изображение в координатах р-V, связь между параметрами, работа и теплообмен, изменение функций состояния.
Изохорный
процесс
(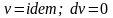 )
– процесс, при котором объем системы
или удельный объем рабочего тела остается
постоянным. В изохорных процессах
происходит увеличение или уменьшение
давления, что связано с соответственным
изменением температуры – подводом или
отводом теплоты.
)
– процесс, при котором объем системы
или удельный объем рабочего тела остается
постоянным. В изохорных процессах
происходит увеличение или уменьшение
давления, что связано с соответственным
изменением температуры – подводом или
отводом теплоты.
Удельная
термодинамическая и потенциальная
работы в изохорном процессе определяются
из соотношений: ,
,
 .
.
Количество
теплоты, подведенной к рабочему телу
или отведенной от него в изохорном
процессе, определяется из выражения
первого начала термодинамики .
.
Изохорный процесс.




19. Изохорный процесс изменения состояния идеального газа. Уравнения процесса, изображение в координатах t-s, связь между параметрами, работа и теплообмен, изменение функции состояния.
Для
идеального газа в изохорном процессе
давление прямо пропорционально
температуре рабочего тела
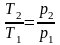 .Первое
начало термодинамики:
.
.Первое
начало термодинамики:
.
Для идеального газа: и
.
20. Изопотенциальный процесс изменения состояния простого тела. Уравнение процесса, изображение в координатах р-V, связь между параметрами, работа и теплообмен, изменение функций состояния.
Изопотенциальный
процесс
–
термодинамический процесс изменения
состояния системы, при котором значение
потенциальной функции
 )
сохраняет неизменное значение.
)
сохраняет неизменное значение.
Удельная термодинамическая и потенциальная работы в изопотенциальном процессе определяются из следующих соотношений:
 =
=
 =
=
 ;
;
 =
=
 =
=
 =
=
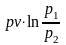 .
.
Нетрудно
заметить, что постоянство потенциальной
функции ( )
приводит к равенству логарифмов в
выражениях в силу того, что соблюдается
условие
)
приводит к равенству логарифмов в
выражениях в силу того, что соблюдается
условие
 .
Поэтому, в изопотенциальном процессе,
численные значения термодинамической
и потенциальной работ равны между собой.
.
Поэтому, в изопотенциальном процессе,
численные значения термодинамической
и потенциальной работ равны между собой.
Количество
теплоты, подведенной к рабочему телу
или отведенной от него, в изопотенциальном
процессе определяется из выражения
первого начала термодинамики по балансу
рабочего тела: .
.
Изопотенциальный процесс.


Так
как
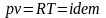 ,
то
,
следовательно, процесс будет также
являться изотермическим.
,
то
,
следовательно, процесс будет также
являться изотермическим.


Для идеального газа:

Первое
начало термодинамики:
.
Если процесс изотермический, то есть
,
следовательно
 .
Для идеального газа
.
Для идеального газа
 ,
тогда:
,
тогда:
 .
.
21,22-Изотермический процесс изменения состояния идеального газа. Уравнение процесса, изображение в координатах T-s, связь между параметрами, работа и теплообмен, изменение функций состояния.
Для идеального газа, согласно уравнению Клапейрона ( ), изопотенциальный процесс ( ) является и изотермическим ( ).
Для идеального газа:
Первое начало термодинамики: . Если процесс изотермический, то есть , следовательно . Для идеального газа , тогда:
.
23,(24).Адиабатический процесс изменения состояния простого тела. Уравнение процесса, показатель процесса, изображение в координатах Р-v, связь между параметрами(Работа и теплообмен, изменение функций состояния. Изображение в координатах работы и теплообмена).
Адиабатный
процесс
-
термодинамический процесс изменения
состояния системы, при котором отсутствует
теплообмен
 и
в силу обратимости процесса энтропия
остается величиной постоянной
и
в силу обратимости процесса энтропия
остается величиной постоянной
 .
.
Из выражения первого начала термодинамики для простого тела при условии имеем
=0
Для
адиабатического процесса
 .
.

Все уравнения для политропного процесса остаются справедливы и для адиабатического процесса, только вместо политропного показателя используют адиабатический показатель.
Для
идеального газа
 и
и





Первое начало термодинамики: . Для идеального газа: и .

 Если
,
то
Если
,
то
 .
Так как
.
Так как
 ,
то достаточно знать одну из работ, чтобы
определить другую.
,
то достаточно знать одну из работ, чтобы
определить другую.
Для
идеального газа:

25,26. Адиабатический процесс изменения состояния идеального газа. Уравнение процесса, показатель процесса, изображение в координатах T-s, связь между параметрами.(Работа и теплообмен, изменение функций состояния. Изображение в координатах работы и теплообмена).
Для идеального газа и
Первое начало термодинамики: . Для идеального газа: и ,
27, (28). Политропный процесс изменения состояния простого тела. Уравнение процесса, показатель процесса, изображение в координатах Р-v, связь между параметрами.(Работа и теплообмен, изменение функций состояния. Изображение в координатах работы и теплообмена.)
Уравнения перечисленных простейших термодинамических процессов могут быть представлены одним уравнением. Это уравнение называется уравнением политропы, а термодинамические процессы, описываемые этим уравнением, называются политропными.
Политропным процессом с постоянным показателем называется обратимый термодинамический процесс изменения состояния простого тела, подчиняющийся уравнению, которое может быть представлено в следующих формах:
 ;
;
 ;
;
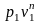 =
=
 ,
,
где п – показатель политропы, являющий в рассматриваемом процессе постоянной величиной, которая может иметь любые частные значения - положительные и отрицательные (- n +). Постоянный показатель политропы определяется соотношением потенциальной и термодинамической работ в элементарном или конечном процессах, либо через параметры состояния
 =
=

Из соотношения следует, что для изобарного процесса – n = 0, для изохорного процесса – n = ± ∞, для изопотенциального процесса – n = 1,для адиабатического процесса – n = k.

Рис. 1.5. Политропные процессы изменения состояния
простого тела

Показателем
политропного процесса является линейная
зависимость
 от
от
 ,
то есть:
,
то есть:
 .
.


1.

2.

Выражения конечных (интегральных) величин термодинамической и потенциальных работ в политропных процессах рассчитываются по следующим соотношениям
 .
.
 ,
,
где
 – характеристика процесса расширения
или сжатия.
– характеристика процесса расширения
или сжатия.
Соотношение
для определения характеристики расширения
или сжатия в рассматриваемом процессе
 определяется с учетом зависимостей и
имеет следующий вид:
=
определяется с учетом зависимостей и
имеет следующий вид:
=
 =
=
 .
.
Расчетное выражения теплообмена для простых тел выводится на основе рассмотрения выражения первого начала термодинамики и имеет следующий вид

 ,
,
где k – показатель адиабаты, n – показатель политропы, nu – показатель изо-энергетического процесса.
Расчетные зависимости показателей термодинамических процессов получаются с использованием дифференциальных соотношений уравнения состояния простого тела
F (р, v, T) = 0:

Если , то есть в случае идеального газа:

При
этом политропный показатель может
принимать значения в пределах от минус
бесконечности до плюс бесконечности и
оставаться постоянным в течение процесса.
Если
 ,
то
,
то
 ,
следовательно
,
то есть процесс изохорический. Если
,
то
,
следовательно
,
то есть процесс изохорический. Если
,
то
 ,
следовательно
,
то есть процесс изобарический. Если
,
то
,
следовательно
,
то есть процесс изобарический. Если
,
то
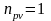 ,
следовательно
.
Так как для идеального газа
,
то
,
следовательно
.
Так как для идеального газа
,
то
 .
.
Если
уравнением процесса является уравнение
,
то в этом процессе
 ,
следовательно
,
следовательно
 ,
то есть процесс изоэнергетический.
,
то есть процесс изоэнергетический.
Для
идеального газа
 ,
следовательно
,
то есть процесс изоэнтальпийный.
,
следовательно
,
то есть процесс изоэнтальпийный.

Работа:
 .
.

 -
для идеального газа.
-
для идеального газа.
Характеристика растяжения (сжатия).
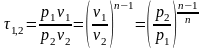
 -
для идеального газа.
-
для идеального газа.

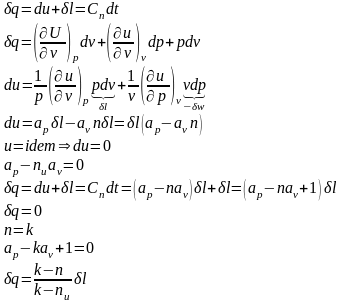
 ,
где
,
где
 - показатель адиабаты,
- политропный показатель,
- показатель адиабаты,
- политропный показатель,
 - показатель изоэнергетического процесса.
- показатель изоэнергетического процесса.
29,(30). Политропный процесс изменения состояния идеального газа. Уравнение процесса, показатель процесса, изображение в координатах T-s, связь между параметрами.(Работа и теплообмен, изменение функций состояния. Изображение в координатах работы и теплоты.)
Если , то есть в случае идеального газа:
- для идеального газа.
- для идеального газа
