Билет №17

Гармоническими называются колебания в любой физической системе, которые описываются величиной, изменяющейся по закону синуса или косинуса.

Кинематические характеристики гармонических колебаний. Найдем величины скорости и ускорения колебательного движения, описываемого уравнением: x = A·sin(w·t + j0). Поскольку скорость u - есть производная от координаты по времени, а ускорение - производная от скорости a = dυ/dt, то для гармонических колебаний, описываемых уравнением, эти величины зависят от времени также по гармоническим законам:u = A·w·cos(w·t + j0) = A·w·sin(w·t + j0 + p/2); a = -A·w2·sin(w·t + j0) = -w2·x. Для гармонических механических колебаний скорость опережает по фазе смещение на p/2, а ускорение - на p. Наличие пропорциональной зависимости ускорения от величины смещения от положения равновесия является характерным признаком гармонического колебательного движения. Циклическая частота w - есть число колебаний осциллятора за 2π секунд: w = 2p/Т, Величина, обратная периоду колебаний Т, называется частотой ν = 1/Т = w/2p. Частота - есть число колебаний осциллятора за одну секунду. Фаза гармонических колебаний Ф линейно растет со временем (см. рис. 11.2). При t = 0 значение Ф равняется j0, которое называется начальной фазой. Начальная фаза задает значение x в начальный момент времени.Начальную фазу и амплитуду гармонического осциллятора можно рассчитать исходя из начальных условий, подставив в уравнение колебательного движения и выражение для его скорости υ = dx/dt значение времени t = 0. Проделав соответствующие операции, получим:х(0) = х0 = А·cos(j0).u(0) = u0 = -А·w·sin(j0).где υ - скорость колеблющейся системы. Решив эту систему уравнений, получим, что величины амплитуды и начальной фазы определяются начальными условиями для рассматриваемой системы. A = (x02 + υ02/ω2)1/2; tg φ0 = -υ0/(x0·ω).

2.

 На этих изотермах хорошо просматривается участок, где давление растёт с ростом объёма. Этот участок не имеет физического смысла. В области, где изотерма делает зигзагообразный изгиб, изобара пересекает её три раза, то есть, имеется три значения объёма V при одинаковых значениях параметров P и T. Это соответствует существованию трёх действительных корней уравнения . При повышении температуры волнообразный участок уменьшается и превращается в точку (см. точка К на рис.). Эта точка называется критической, а значения , и в этой точке называются критическими параметрами. Критической точке соответствуют три совпадающих корня уравнения. При температурах, превышающих критическую, изотермы Ван-дер-Ваальса становятся монотонно убывающими функциями P(V). Критические параметры , и можно найти из условия, что в критической точке изотерма Ван-дер-Ваальса имеет как экстремум, так и точку перегиба: , . Решая эти два уравнения совместно с можно получить , ,

Билет № 20

1.Механическими колебаниями называют движения тел, повторяющиеся точно или приблизительно через одинаковые промежутки времени.

Свободные механические колебания всегда оказываются затухающими, те колебаниями с убывающей амплитудой.

Диф. Уравнение затухающих колебаний: , где , а .

Амплитуда колебаний постепенно уменьшается, и через некоторое время после начала колебаний становится равной нулю.

Коэффициент затухания – скорость затухания колебаний, определяемая величиной β=r/2m. Коэффициент затухания обратен по величине тому промежутку времени, за который амплитуда уменьшилась в е раз. (βτ=1, где τ , время, за которое амплитуда уменьшится в е раз.)

Отношение значений амплитуд,

соответствующих моментам времени, отличающимся на период, равно a(t) / a(t+T)= e^βT

Это отношение называют декрементом затуха­ния, а его логарифм — логарифмическим де­крементом затухания:Λ=lna(t)/a(t+T)=βT

Последнюю величину обычно используют для характе­ристики затухания колебаний. Выразив β через λ и Т в соответствии с (73.12), закон убывания амплитуды можно записать в виде а = а₀ е ^{-λ/T· t}За время т, за которое амплитуда уменьшается в е раз, система успевает совершить N_e = τ/Т колебаний.Из условия е ^-λ·τ/T =е^-1 получается, что λ·τ/T = λN_e = 1.Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз.

2.

Взаимодействие между молекулами реального газа обусловливает их взаимную потенциальную энергию Е_р, которая входит во внутреннюю энергию газа наряду с кинетической энергией движения молекул E_h:

U= E_k+E_p

При расширении газа должна быть совершена рабо­та по преодолению сил притяжения между молекулами. Как известно из механики, работа против внутренних сил идет на увеличение потенциальной энергии системы. Подобно тому как работа против внешних сил опреде­ляется выражением d'A = p dV, работа против внутрен­них сил, действующих между молекулами киломоля га­за, может быть записана в виде d'A — p_idV_KM, где pi —■ внутреннее давление, равное в случае ван-дер-вааль-совского') газа a/V ²_км.Приравняв d'A приращению

взаимной потенциальной энергии молекул dh_p, получим:

dE_p = p_idV_км = a/V²_км·dV_км

2 Интегрирование этого выражения дает для потенци­альной энергии

E_р = - a/V_км + const.

Значение постоянной интегрирования следует вы­брать так, чтобы выражение для внутренней энергии U в пределе, при возрастании объема до бесконечности, переходило в выражение для внутренней энергии иде­ального газа (напомним, что при увеличении объема все реальные газы приближаются по своим свойствам к иде­альному газу). Исходя из этих соображений, постоян­ную интегрирования нужно положить равной нулю. Тогда для внутренней энергии реального газа полу­чается следующее выражение: U_KM = C_VT-a/V_км

из которого следует, что внутренняя энергия растет как при повышении температуры, так и при увеличении объема.

Если газ будет расширяться или сжиматься без теп­лообмена с внешней средой и без совершения внешней работы, то согласно первому началу термодинамики его внутренняя энергия должна оставаться постоянной. Для газа, энергия которого определяется формулой (121.1), должно при этом соблюдаться условие

dU_км=C_VdT +a/V²_км dV _км= 0

откуда следует, что dТ и dV_KM имеют разные знаки.

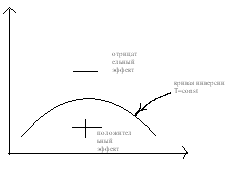
Следовательно, при расширении в таких условиях газ должен всегда охлаждаться, а при сжатии—нагре­ваться. 122. Эффект Джоуля — Томсона Пропуская газ по теплоизолированной трубке с по­ристой перегородкой, Джоуль и Томсон обнаружили, что при расширении, которым сопровождается прохож­дение газа через перегородку, температура его несколько изменяется. В зависимости от начальных давления и температуры изменение температуры ∆T имеет тот или иной знак и, в частности, может оказаться равным нулю. Это явление получило название эффекта Джоуля — Том-сона. Если температура газа понижается (∆T<0), эф­фект считается положительным; если газ нагревается (∆T>0), эффект считается отрицательным. Отметим, что эффект Джоуля — Томсона всецело обусловлен отклонениями газа от идеальности. Для иде­ального газа pV = RT и условие (122.2) превращается в T_t + RT,=C_VT₂ + RT₂, откуда следует, что Т₁ = Т₂.