26. Расчет переходных процессов методом переменных состояния.

Одним из матричных методов анализа переходных процессов сложных электрических цепей является метод переменных состояния, основанный на использовании двух матричных уравнений.

Метод переменных состояния должен включать:

1 . алгоритм формирования уравнений (1)

(2) y = Cx + Dυ.

2. алгоритм решения уравнений состояния как задачи Коши применительно к классу входных воздействий.

С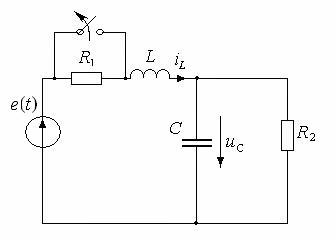 оставить уравнение состояния цепи после коммутации.

Решение: Уравнение состояния ,

Вектор-столбец переменных состояния ,

вектор-столбец первых производных .

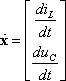В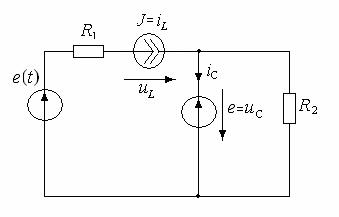 ектор столбец входных воздействий υ(t) = [e(t)]. Применим теорему компенсации, заменив накопители эквивалентными источниками:

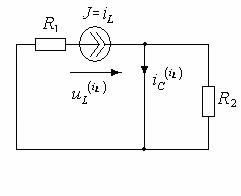
По методу наложения

u_L = u_L^iL + u_L^uC + u_L^e, i_C = i_C^iL + i_C^uC + i_C^e.

Ч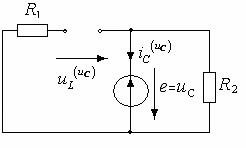 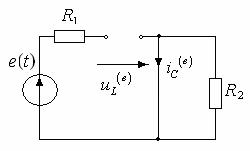астичные схемы:

Напряжение на катушке по методу наложения: .

Ток в конденсаторе: .

Уравнение состояния имеет вид:

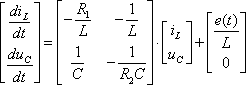
Решение матричного уравнения можно представить в виде суммы свободной х_св и принужденной х_прин составляющих: (3),

где е^At — матричная экспонента. При постоянном входном воздействии, т.е. когда υ(t) = const уравнение принимает вид:

x = х_св + х_прин = е^At*х₀ + (е^At – 1)·A–1·B·υ

и решение сводится к нахождению матричной экспоненты. Существует несколько способом нахождения матричной экспоненты, например с помощью ряда:

В случае, когда все собственные числа α_k, k = 1,2…n различны (простой спектр), выражение матричной экспоненты имеет вид: где Рk, k = 1,2,…n — квадратные матрицы, называемые проекторами матрицы А:

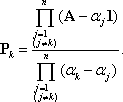
Тогда и решение (3) уравнения состояния (1) можно выразить через обычные экспоненциальные функции

27. Формирование уравнений состояния в методе переменных состояния.

П ри использовании метода переменных состояния вначале составляется уравнение состояния, запись которого представляет собой нормальную форму обыкновенного дифференциального уравнения:

Здесь x = x(t) = [x₁(t) x₂(t)…x_n(t)]^T – вектор-столбец переменных состояния x_j, в качестве которых выбираются токи i_Lj индуктивных и напряжения u_Cj емкостных элементов, υ = υ(t) = [υ₁(t) υ₂(t)…υ_m(t)]^T — вектор-столбец э.д.с и токов источников тока цепи, А и В — соответственно nx_n и nx_m-матрицы, коэффициенты которых выражаются через параметры накопительных и резистивных элементов. Второе уравнение связывает переменные состояния с искомыми переходными токами и напряжениями и входными переменными: y = Cx + Dυ.

Здесь y = y(t) = [y₁(t) y₂(t)…y_k(t)]^T — вектор-столбец выходных переменных y_j, С и D — соответственно nx_k и kx_m–матрицы.

Для составления уравнений состояния достаточно учесть, что производные весьма просто выражаются через напряжения индуктивных и токи емкостных элементов, а именно:

Тогда для определения производных, т.е. производных достаточно найти линейную связь между каждым из напряжений индуктивных элементов u_Lj, а также каждым током емкостных элементов i_Cj и всеми переменными состояния. Уравнения состояния можно формировать по специально разработанным алгоритмам. Наиболее целесообразен способ формирования уравнений состояния, основанный на использовании принципа компенсации и метода наложения. Накопители в цепях заменяют соответственно источником тока для индуктивного элемента J = i_L(t) и источником э.д.с для емкостного элемента e = u_C(t). Полученные резистивные цепи эквивалентны исходным цепям, но описываются чисто алгебраическими уравнениями.