
- •1. Параметры и закономерности прямолинейного движения мт.
- •2. Криволинейное движение материальной точки.
- •3. Основные законы поступательного движения
- •4. Принципы суперпозиций и относительность движение мт.
- •1. Принцип относительности Галилея
- •5. Работа и энергия и их эквивалентность.
- •9. Колебательные движения материальной точки.
- •12. Законы сохранения в механике мт.
- •13. Условия равновесного состояния тел.
- •14. Параметры и основной закон вращательного движения.
- •15. Методика определения момента инерции тела (на примере точки). Теорема Штейнера.
- •16. Закон сохранения для вращательного движения.
- •17. Колебательное движение твердого тела, определение частоты колебаний.
- •18. Степени свободы механического движения системы тел. Закон равнораспределения энергии для газа.
- •21. Теплопроводность газа.
- •22. Внутреннее трение в газе
- •23. Диффузия в газе.
- •19. Максвелловское распределения молекул газа по скоростям.
- •24. Закон сохранения энергии для изотермического и адиабатического.
- •27. Термодинамические циклы, кпд тепловых машин.
- •25. Работа газа и его теплоемкость при изо- и адиабатных процессах.
- •26. Уравнение Пуасона, уравнение политропического процесса.
- •29. Молекулярно-кинетический смысл энтропии.
- •20. Больцмановское распределение молекул газа.
- •31. Уравнение состояния газа и его применение.
- •10. Явление резонанса при колебании мт.
2. Криволинейное движение материальной точки.
Пусть
материальная точка совершает движение
по окружности радиусом
R.
Выберем систему координат, плоскость
XOY
которой совпадает с плоскостью
движения материальной точки, а начало
координат совпадает с центром окружности,
описываемой материальной точкой (рис.
1.7). Скорость движения материальной
точки
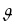 ,
направленная по касательной к траектории,
всегда перпендикулярна радиус-вектору
материальной точки
,
направленная по касательной к траектории,
всегда перпендикулярна радиус-вектору
материальной точки
 ,
а величина радиус-вектора
,
а величина радиус-вектора
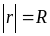 не меняется со временем.
не меняется со временем.
П ри
движении материальной точки по окружности,
кроме скорости
,
которую часто называют линейной
скоростью,
удобно использовать понятие угловой
скорости материальной точки w.
ри
движении материальной точки по окружности,
кроме скорости
,
которую часто называют линейной
скоростью,
удобно использовать понятие угловой
скорости материальной точки w.
Средней
угловой скоростью <w>
материальной точки на данном участке
движения называется величина,
равная отношению угла поворота Dj
радиус-вектора
точки за некоторый промежуток времени
Dt
к этому промежутку времени:
 ,
а угловую скорость w
определим, как предел, к которому
стремится <w>
при Dt
®
0:
,
а угловую скорость w
определим, как предел, к которому
стремится <w>
при Dt
®
0:
 (32),
где
dj
– угол, на который поворачивается
радиус-вектор материальной точки
за бесконечно малый промежуток времени
dt.
Легко найти связь между угловой скоростью
w
и модулем линейной скорости u
материальной точки. За время dt
материальная точка пройдет путь
dS
по дуге окружности радиусом R
(см. рис. 1.7), причем dS=
Rdj
(33). Очевидно, что, независимо от характера
движения, путь DS,
пройденный точкой за промежуток времени
Dt,
будет равен DS
= RDj,
где Dj
– угол поворота радиус-вектора точки
за этот промежуток времени.
(32),
где
dj
– угол, на который поворачивается
радиус-вектор материальной точки
за бесконечно малый промежуток времени
dt.
Легко найти связь между угловой скоростью
w
и модулем линейной скорости u
материальной точки. За время dt
материальная точка пройдет путь
dS
по дуге окружности радиусом R
(см. рис. 1.7), причем dS=
Rdj
(33). Очевидно, что, независимо от характера
движения, путь DS,
пройденный точкой за промежуток времени
Dt,
будет равен DS
= RDj,
где Dj
– угол поворота радиус-вектора точки
за этот промежуток времени.
Поскольку величина линейной скорости v=dS/dt (34) то, подставив (33) в (34) с учетом (32), получим v =Rdj/dt=Rw (35)
Угловым
ускорением
e
материальной точки называется величина,
равная пределу, к которому стремится
отношение приращения угловой скорости
Dw
за промежуток времени Dt
к этому промежутку времени при стремлении
последнего к нулю
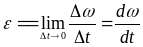 (36)
(36)
т.е. производной от угловой скорости по времени.
Из (36) видно, что e > 0, если угловая скорость материальной точки w увеличивается со временем, e < 0, если угловая скорость уменьшается со временем, и e = 0, если w = const.
Используя соотношения (35) – (36), можно найти нормальное an и тангенциальное at ускорения материальной точки при ее движении по окружности радиусом R: an=v2/ R=w2R (37) и an=dv/dt=R (dw/dt)=Re (38).
Из (38) следует, что тангенциальное ускорение характеризует быстроту изменения численного значения скорости МТ. При равномерном движении at=0. Если at>0, то движение называют ускоренным, если at<0 – замедленным. Наконец, если at=const, то движение называют равнопеременным: за равные промежутки времени численное значение скорости изменяется на одну и ту же величину.
Нормальное ускорение характеризует быстроту изменения направления вектора скорости материальной точки. Если движение прямолинейное, то an=0.
Тогда
полное ускорение материальной точки:
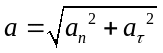
3. Основные законы поступательного движения
Д вижение
твердого тела называют поступательным,
если любая прямая, жестко связанная с
телом, перемещается, оставаясь
параллельной ее первоначальному
направлению (рис. 1.7). Поступательно
движутся относительно земли, например,
кабина лифта, резец токарного станка,
пассажирские кабины «колеса обозрения»,
стрелка компаса при любом перемещении
его корпуса в горизонтальной плоскости
и т. д.
вижение
твердого тела называют поступательным,
если любая прямая, жестко связанная с
телом, перемещается, оставаясь
параллельной ее первоначальному
направлению (рис. 1.7). Поступательно
движутся относительно земли, например,
кабина лифта, резец токарного станка,
пассажирские кабины «колеса обозрения»,
стрелка компаса при любом перемещении
его корпуса в горизонтальной плоскости
и т. д.
При поступательном движении тела траектории АА' и ВВ' любых двух его точек А и В (рис. 1.7) совершенно идентичны: их можно полностью совместить путем параллельного переноса вдоль прямой АВ. Поэтому приращения радиусов-векторов всех точек тела за любой произвольно выбранный промежуток времени одинаковы. Следовательно, в любой момент времени все точки тела имеют одинаковые скорости и ускорения, а кинематическое рассмотрение поступательного движения абсолютно твердою тела сводится к изучению движения любой из его точек.
Свободно движущейся материальной точкой или свободной материальной точкой (телом) можно назвать материальную точку, действием на которую других точек можно пренебречь. Если с такой точкой (телом) связать систему отсчета, то в такой системе движение других свободных тел выглядит особо просто: оно происходит прямолинейно и равномерно, то есть с постоянной по величине и направлению скоростью ( =const). Это утверждение составляет содержание закона инерции. Система отсчета, связанная со свободным телом, называется инерциальной системой отсчета. Закон инерции констатирует факт существования инерциальных систем отсчета и носит название Первого закона Ньютона: если результирующая сила, действующая на материальную точку (тело) равна нулю, то тело покоится или совершает равномерное и прямолинейное движение. Следствие 1: состояние покоя и равномерное прямолинейное движения не различимы. Следствие 2: Ньютон вводит понятие причины вызывающее изменение состояние движение – СИЛА. Следствие 3: Сколько сил бы не действовало, их можно свести к равнодействующей (результирущей) - это и есть принцип суперпозиций.
Однако характер движения не будет зависеть от выбора. В этом суть одного из фундаментальных законов физики – принципа относительности. Следует понимать, что все используемые в физическом эксперименте системы отсчета являются инерциальными лишь с большей или меньшей степенью точности. Например
Второй
закона Ньютона
в инерционной системе отсчетов (скорость
изменения импульса точки равна
равнодействующей силе, действующей на
точку):
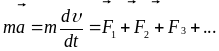 ,
гд е
m
– масса материальной точки;
,
гд е
m
– масса материальной точки;
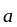 -
ускорение
этой материальной точки;
-
ускорение
этой материальной точки;
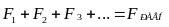 сумма
всех сил,
действующих на эту материальную точку.
сумма
всех сил,
действующих на эту материальную точку.
 -
импульс тела.
-
импульс тела.
ИСО системы отсчета, относительно которых любая материальная точка, свободная от действия сил, не имеет ускорения.
Инерциальной может приближенно считаться:
• Система отсчета, связанная с поверхностью Земли (если не требуется учитывать вращение Земли и силы притяжения к Солнцу и планетам)
• Система отсчета, с центром в центре Земли, оси которой направлены на звезды (если надо учесть вращение Земли вокруг своей оси, но вращение вокруг Солнца и притяжение к Солнцу и планетам можно не учитывать).
• Система отсчета, с центром в центре Солнца, оси которой направлены на звезды (если можно не учитывать вращение солнечной системы вокруг ядра галактики и притяжение к другим звездам).
Третий
закона Ньютона:
с какой силой тело 1 действует на тело
2, с такой же силой, но противоположной
по направлению, тело 2 действует на тело
1:
 .
.
Следствие 1: Взаимодействие двух тел можно заменить действием одного тела на другое.
