25. Работа газа и его теплоемкость при изо- и адиабатных процессах.

Так, при изохорном процессе dV = 0, т.е. работа А = 0 и вся теплота идет на изменение внутренней энергии газа CmdT=dU, где dU=imRdT/2M, откуда теплоемкость газа при изохорном процессе

R – универсальная газовая постоянная

Во всех других процессах объем газа изменяется. При изобарном процессе работа газа

, или .

Теплоемкость газа при изобарном процессе

.

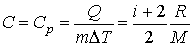Молярные теплоемкости газа при постоянном объеме и постоянном давлении

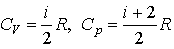
Уравнение Майера связывает молярные теплоемкости газа при изохорном и изобарном процессах Cp=Cv+R.

При изотермическом процессе температура газа постоянна, поэтому количество теплоты идет на совершение работы dQ=dA , где dA=pdV. Работа вычисляется интегрированием

.

Адиабатный процесс реализуется в условиях теплоизоляции системы, но адиабатным можно считать также процесс, протекающий столь быстро, что за время его осуществления не успевает произойти существенный теплообмен с внешней средой. Из первого начала термодинамики следует, что в адиабатном процессе работа совершается за счет изменения внутренней энергии: dA=-dU. Т.е. если газ расширяется, то его температура понижается, а при резком сжатии – нагревается. Работа при адиабатном процессе противоположна по знаку изменению внутренней энергии

26. Уравнение Пуасона, уравнение политропического процесса.

Поскольку при любом процессе для идеального газа pV/T=const, то давление и объем связаны соотношением

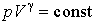. (2)

Соотношение (2) называют уравнением Пуассона.

Политропическими называются процессы, при которых теплоемкость тела остается постоянной. Для идеального газа уравнение политропы имеет вид:

,

где n – показатель политропы

.

Рассмотренные ранее процессы относятся к категории политропических. Изобарическому процессу соответствует n = 0, изотермическому – n = 1, адиабатическому n = g.

29. Молекулярно-кинетический смысл энтропии.

Существует связь второго закона термодинамики с молекулярно-кинетической теорией строения вещества. Раскрытие этой связи позволяет глубже понять физический смысл энтропии.

С молекулярно-кинетической точки зрения каждому состоянию газа (системы частиц) соответствует некоторое распределение его молекул по объему, а также по скоростям (импульсам и энергиям). Предположим, что система, изолированная от внешней среды, содержит 4 частицы (n = 4) и занимает объем V (рис. 3.4).

Предположим, что частицы «меченные», а объем разбит на две равные части. Будем считать, что различные состояния отличаются только распределением молекул 1, 2, 3, 4 по двум ячейкам. Представим в виде таблицы все возможные состояния такой системы.

Макросостояние	Возможные микросостояния*	Г, Число микросостояний	w, Вероятность макросостояния
1. Справа нет частиц	0000	1	1/16
2. Справа одна частица	1000 0100 0010 0001	4	4/16
3. Справа две частицы	1100 1010 1001 0110 0101 0011	6	6/16
4. Справа три частицы	0111 1011 1101 1110	4	4/16
5. Справа четыре частицы	1111	1	1/16

 Примечание. * Если частица находится слева, это обозначено цифрой «0», если справа – «1».

Состояния, перечисленные в одной строке, в макро-масштабе неразличимы и обладают одинаковой энергией. Число микросостояний определяется соотношением 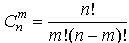. Число микросостояний, с помощью которого реализуется данное макросостояние, называется статистическим весом Г или кратностью вырождения макросистемы. Из таблицы видно, что статистический вес Г и вероятность состояния одновременно достигают максимального значения. Минимальной вероятностью обладает состояние, реализуемое единственным способом. Рассмотрим сосуд, в котором содержится N_A частиц, и они занимают объем V₀. Выделим внутри малый объем V. Вероятность обнаружить там одну частицу w₁= V/V₀, вероятность встретить там две частицы w₂= (V/V₀)², вероятность там встретить все N_A частиц w_Na= (V/V₀)^Na. (4)

Поскольку выделенный объем мал, то вероятность w_Na<<1, поэтому состояние никогда не реализуется. Для этого состояния статистический вес равен Г=1, т.е. состояние реализуется единственным способом. Прологарифмируем выражение (4)

.

Сравним это выражение с соотношением, полученным ранее для энтропии (для одного моля):

.

Можно записать S~klnw_Na. Поскольку вероятность состояния w~Г, то между энтропией системы и статистическим весом ее состояния существует связь, которая описывается формулой Больцмана S~klnГ. Данная формула позволяет дать статистическое толкование второго начала термодинамики. Для реальных процессов ∆S>=0, следовательно, замкнутая термодинамическая система переходит из состояний менее вероятных в состояния более вероятные, пока не достигнет равновесного состояния, которое является наиболее вероятным. Иными словами, второе начало термодинамики имеет статистический характер, выражающий стремление системы, состоящей из большого количества частиц, к самопроизвольному переходу из состояний менее вероятных в состояния более вероятные.

К системам с малым количеством частиц второй закон термодинамики неприменим. Так в сильно разреженных газах происходят значительные случайные отклонения от равномерного распределения молекул по объему. Подобные явления называются флуктуациями (отклонения параметров от средних значений, например, плотности, температуры, давления). Флуктуации обусловлены тепловым движением частиц макросистемы. Можно показать, что в газе относительная флуктуация концентрации 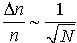, где N – количество частиц. Если в сосуде N ~ 10²³ частиц, то ∆n/n=10^-12. Видно, что вероятность заметных отклонений параметров газа от средних величин ничтожно мала.

30. Длина свободного пробега частиц в газе.

При столкновении частиц газа изменение направления движения (относительного) их, происходит, можно считать, в момент сближения их до расстояния d и, следовательно, эта величина может быть взята для характеристики размеров сталкивающихся молекул.

Перейдем далее к определению числа столкновений частиц газа за 1 секунду. Для этого предположим, вначале, что все частицы в газе кроме одной неподвижны, а движущаяся частица имеет скорость, равную средней тепловой . Очевидно, что за единицу времени (секунду) движущаяся частица столкнется со всеми частицами, центры которых лежат внутри цилиндра радиусом R. Движущаяся частица столкнется со всеми частицами, центры которых лежат в цилиндре с площадью и длиной .

.

Учтем движение всех частиц. Вдоль х движение не скажется на числе столкновений, т.к. сколько частиц «убегает», столько же и движется «навстречу».

Найдем относительную скорость частиц, движущихся перпендикулярно х:

,

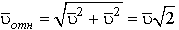тогда

.

За 1 с частица проходит расстояние , поэтому средняя длина свободного пробега равна

.

Зависимость l от Т (формула Сезерленда) имеет вид

,

где С – постоянная Сезерленда.