18. Степени свободы механического движения системы тел. Закон равнораспределения энергии для газа.

Числом степеней свободы тела называют наименьшее число коор­динат (число независимых координат), которые необходимо задать для того, чтобы полностью определить положение тела в пространстве. Так, например, материальная точка, свободно движущаяся в простран­стве, обладает тремя степенями свободы (координаты х; у и z).

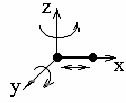Абсолют­но твердое тело имеет шесть степеней свободы: для определения его положения в пространстве нужно задать три координаты центра масс тела, две координаты, определяющие положение в пространстве опре­деленной оси, проходящей через центр масс и какую-либо другую фик­сированную точку тела, и, наконец, нужно еще задать угол поворота тела вокруг этой оси по отношению к некоторому начальному положе­нию. Следовательно, абсолютно твердое тело обладает тремя степеня­ми свободы поступательного движения и тремя степенями свободы вра­щательного движения.

Если тело не абсолютно твердое и его части могут смещаться друг относительно друга, то необходимо вводить еще дополнительные сте­пени свободы колебательного движения.

Закон Больцмана о равномерном распределении энергии по степеням свободы (закон равнораспределения)

Число независимых параметров, задающих состояние системы.

Число степеней свободы i	Одноатомный газ	Двухатомный газ	Многоатомный газ
поступательное	3	3	3
вращательное	-	2	3
Всего	3	5	6

Для системы находящейся в состоянии термодинамического равновесия на каждую поступательную или вращательную степень свободы приходится в среднем кинетическая энергия равная кТ/2, а на каждую колебательную степень свободы в среднем энергия равна кТ.

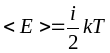
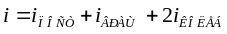
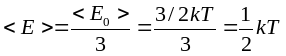_{- с неупругими связями}

Закон равномерного распределения энергии по степеням свободы приводит к выводу о том, что все степени свободы молекулы рав­ноправны и вносят одинаковый вклад в ее среднюю энергию. Вы­вод о полной равноправности всех степеней свободы связан с некоторы­ми общими положениями классической физики, которые в действитель­ности имеют ограниченную область применимости.

21. Теплопроводность газа.

Теплопроводность имеет место тогда, когда в газе сущест­вует разность температур, вызванная какими-либо внешними причина­ми. Молекулы газа в разных местах его объема имеют разные средние кинетические энергии. Поэтому при хаотическом тепловом движении молекул происходит направленный перенос энергии. Молекулы, попавшие из нагретых частей газа в более холодные, отдают избыток своей энергии окружающим частицам. Наоборот, медленно движущиеся молекулы, попадая из холодных частей в более горячие, увеличивают свою энергию за счет соударений с молекулами, обла­дающими большими скоростями.

1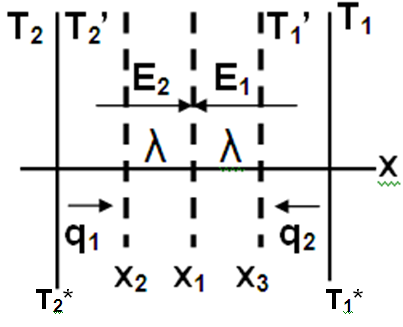 ) λ<<α E₁>E₂

Здесь газ заключен между двумя ограничивающими его стенками с различными температурами Т₁ и Т₂. Выделим в пространстве между стенками воображаемую поверхность х₁ и х₂ и х₃ параллельные ей на расстоянии от х₁ равном средней длине свободного пробега 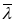. У стенки с Т₁ газ нагрет до Т₁, а у стенки с Т₂ до Т₂. Пусть Т₁ > T₂, тогда очевидно в газе будет происходить изменение температуры газа от Т₁ до Т₂, т.е. вдоль x будет существовать изменение температуры, которое в каждой точке x можно характеризовать бесконечно малыми приращениями dT и dx. Отношение dT/dx называется градиентом температуры.

Пусть на х₃ температура газа соответствует Т₁*, а на х₂ – Т₂* при хаотическом тепловом движении через площадку х₁ частицы газа, движущиеся от х₃ к х₁ будут переносить среднюю кинетическую энергию, соответствующую Т₁*, а движущиеся со стороны х₂ – среднюю кинетическую энергию, соответствующую Т₂*. Это утверждение будет справедливым, т.к. на длине свободного пробега скорость частиц не изменяется. Полный поток энергии, переносимый через плоскость S можно определить как разность потоков переносимой частицами энергии слева направо и справа налево. Считая движение частиц газа хаотическим (равновероятным во всех направлениях), для потоков частиц слева направо и справа налево можем записать что поток энергии (тепловой поток) равен q=-ædТ/Dx (Экспериментальный закон Фурье), где æ – коэффициент теплопроводности вещества, α – расстояние между стенками с различной температурой

П

Т₂*

Т₁*

оток энергии – q=q2-q1 (поток – величина переносимого параметра приходящегося на единицу площади в единицу времени).

При теплопроводности переносимой величиной является энергия E=mv²/2.

Каждая частица двигаясь с права на лево имеет большую энергию чем с лева на право.

q=N(E₁-E₂), где N – число частиц в единицу времени на единицу площади.

æ=1/3ρVλС*_v и Q=æSt.

Где С*_v – величина, характеризующая, как изменяется средняя энергия молекул газа с изменением температуры, т.е. теплоемкость газа.

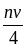
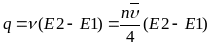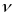2) α<=λ – то при движении между стенками частицы газа сталкиваться не будут, поэтому процесс теплопроводности будет осуществляться иначе: прямым переносом энергии частицами газа от стенки с Т₁ на стенку Т₂. В этом случае поток частиц на стенку (и со стенки) равен , где – поток на стену