20. Больцмановское распределение молекул газа.

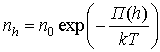
Где концентрация на уровне z=0. Это выражение является распределением Больцмана, характеризующим распределение концентрации частиц в потенциальном поле. Это выражение определяет распределение частиц в потенциальном поле при максвелловском распределении этих частиц по скоростям.

Из распределения Больцмана следует, что частицы с большей плотностью располагается там, где ниже их потенциальная энергия, а также там, где выше температура.

В поле силы тяжести П(h)=mgh, а p=nkT поэтому можем записать барометрическую формулу для распределения давления воздуха по высоте

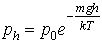, (24)

где p₀ – давление газа поверхности Земли.

Практическое подтверждение вытекающей из закона Больцмана барометрической формулы показывает, что максвелловское распределение частиц газа по скоростям является универсальным, т.е. пригодным для систем с наложенным и без наложенного силового поля, поскольку потенциальное поле сил не изменяет вид функции распределения Максвелла по любой из проекций скоростей частиц газа.

31. Уравнение состояния газа и его применение.

Реальный газ хорошо описывается уравнением Менделеева-Клапейрона:

где R – молярная газовая постоянная, n =m/M - количество вещества (M - молярная масса газа, m - масса газа). Но только при малых плотностях, т.е. при небольшом давлении и достаточно высоких температурах. С повышением давления и уменьшением температуры наблюдается значительное отступление от уравнения Менделеева – Клапейрона.

Самым простым и вместе с тем дающим хорошие результаты при описании газов в широком интервале плотностей, оказалось уравнение Ван-дер-Ваальса

,

где p – давление газа, V_m – молярный объем; а и b – постоянные Ван-дер-Ваальса, имеющие для разных газов различные значения. Поправка характеризует ту добавку к внешнему давлению, которая обусловлена взаимным притяжением молекул друг к другу. Вследствие того, что молекулы обладают конечным объемом, пространство, доступное для движения молекул, оказывается меньшим, чем объем сосуда V_m. Поправка b характеризует ту часть объема, которая недоступна для движения молекул. Уравнение можно переписать для произвольной массы m, учитывая, что V = nV_m

,

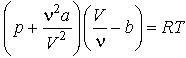где n =m/M – количество вещества. Записываем уравнение для n молей газа

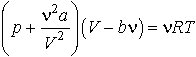. (5)

Реальные газы следуют уравнению Ван-дер-Ваальса лишь приближенно. Воображаемый газ, точно подчиняющийся уравнению (5), называется ван-дер-ваальсовским.

10. Явление резонанса при колебании мт.

Резонанс – явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте равной или близкой собственной частоте колебательной системы.

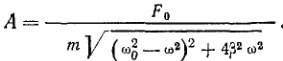
Амплитуда установившихся вынужденных колебаний прямо про­порциональна амплитуде вынуждающей силы F₀ обратно пропор­циональна массе т системы и уменьшается с увеличением коэффи­циента затухания β. При постоянных F₀, т и β амплитуда зависит только от соотношения циклических частот вынуждающей силы w и свободных незатухающих колебаний системы w₀. Рис. 8.19 позво­ляет определить сдвиг фаз φ₀ между скоростью установившихся вы­нужденных колебаний и вынуждающей силой, а также сдвиг фаз α=φ₀-π/2 между смещением и вынуждающей силой.

А_рез=f₀/2βw₀