
- •1)Полярная система
- •5)Кривые второго порядка
- •11)Размерность и базис линейного пространства, координаты вектора
- •14.Пусть плоскость q проходит через точку м0 (x0 ,y0 ,z0 ) перпендикулярно вектору
- •15) Угол между плоскостями
- •17)Матрицы
- •18)Определители
- •23)Решение системы линейных уравнений матричным методом
- •25) Теорема Кронекера – Капелли
- •28)Экономическая интерпретация числа е
- •29)Функции и отображения их области опред. И знач.
- •32) Односторонний предел
- •33)Бесконечно малые величины и их св-ва
- •34)Непрерывность функции в точке.
- •35)Непрерывность сложной функции и обратной функции.
- •37)Определение Производной
- •39)Производные основных элементарных функций.
- •40 Дифференциал функции.
- •41. Производные и дифференциалы высших порядков
- •2)Теорема Ферма и Ролля.
- •44.Условия постоянства функции
- •45.Экстремумы функции
- •46.)Условие выпуклости и вогнутости функции. Точка перегиба.
- •47).Асимптоты.
- •48)Функ. Нескольких переменных
- •52)Первоообразная функции и неопределённый интеграл
- •53)Метод замены переменной
- •55)Интегрирование простейших рац. Дробей
- •56)Интегрирование рациональных дробей
- •57)Интегрирование тригонометрических функций
- •58)Определенный интеграл.
- •59.)Основные свойства определённого интеграла
- •61.)Применение определённого интеграла для вычисления площадей фигур, длин дуг плоских кривых и объёмов тел.
- •62.)Несобственные интегралы
- •66)Неоднородными дифференциальным урав. Второго порядка с постоянными коэффициентами наз. Уравнение вида , где p и q- постоянные, – функ., непрерывная на некотором множестве х.
- •68).Признаки сходимости рядов с положительными членами
40 Дифференциал функции.
Пусть
функция y
= f(x)
имеет конечную производную в точке х:
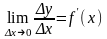 ,
то
,
то
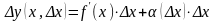 ,
где 0,
при х0.
f(x)x-
линейная часть приращения и называется
дифференциалом функции и обозначается
dy
df(x).
dy
= f(x)dx.
Можно
также записать:
,
где 0,
при х0.
f(x)x-
линейная часть приращения и называется
дифференциалом функции и обозначается
dy
df(x).
dy
= f(x)dx.
Можно
также записать:
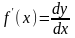
Применение дифференциала к приближенным вычислениям.
Дифференциал функ. y = f(x) зависит от х и явл. главной частью приращения х.
Приращение ∆у функ. у=ƒ(х) в точке х можно представить в виде ∆у=ƒ'(х)•∆х+α•∆х, где α→0 при ∆х→0, или ∆у=dy+α•∆х. Отбрасывая бесконечно малую α•∆х более высокого порядка, чем ∆х, получаем приближенное равенство
∆у≈dy, ƒ(х+∆х) ≈ ƒ(х)+ƒ'(х) ∆х причем это равенство тем точнее, чем меньше ∆х.
Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функ.
Дифференциал обычно находится значительно проще, чем приращение функ., поэтому формула широко применяется в вычислительной практике.
41. Производные и дифференциалы высших порядков
:
Производная второго порядка называется
производная производной данной функции: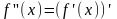
Определение:
Производная
n-го
порядка называется производной
производной n-1-го
порядка.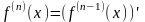
Используя метод математической индукции несложно показать, что:
1). n-ая производная обладает свойством линейности, т.е.:
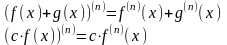
2).
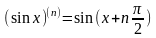
3).
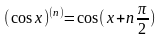
4).
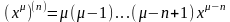
5).
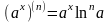
6).
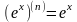
y= f(x)
f (x)=
(x)=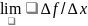 =
(x)
=
(x)
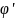 (x)
=
(x)
=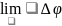 /
/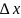
(x)=
(f
(x))
=f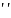 (x)
(x)
f = df/dx f =d2f/dx2
Можно определить производную любого порядка.
d2 y = d(dy)=d(f (x)* dx)
dy=y (x)*dx
d2 y= f (x)* dx2
dn y=f(x) n *(dx)n
42)Стационарные точки.
Стационарная
точка (или кривая), точка (кривая), в
которой дифференциал функции (вариация
функционала) обращается в нуль. Для
функции одного переменного у = f (x)
касательная в Стационарная точка к
графику функции параллельна оси Ох,
касательная плоскость к поверхности Z
= f (x, у) в Стационарная точка функции
двух переменных f (x, у) параллельна
плоскости хОу.
2)Теорема Ферма и Ролля.
Ферма: Пусть y=f(x) дифференцируется на некотором множестве X.
Пусть некоторая точка этого множества в некоторой точке этого множества функ. достигает своего наибольшего или наименьшего значения, тогда производная в этой точке = 0.
Ролля: Теорема Ро́лля утверждает, что если функ., имеющая производную на интервале, принимает в его концах равные значения, то её производная обращается в нуль в некоторой точке внутри интервала.
Пусть
1)y=f(x)
определена и непрерывна на интервале
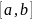
2)”y”
дифференцируема по крайней мере на
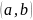
3)в концах отрезка f принимает одинаковое значение f(a)=f(b).
Тогда сущ. по крайней мере одна внутренняя точка, где производная =0.
Теорема Лагранжа.
1.y=f(x) определена и непрерывна на .
2.y=f(x) дифференцируема по крайней мере на (a,b).
Тогда сущ. по крайней мере одна точка z где производная равна
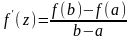 .
.
43)
Правило
Лопиталя.
Пусть функ. f(x) и g(x) дифференцируемы
в некоторой окрестности точки a,
за исключением, быть может, самой точки a,
и пусть ![]() или
или ![]() .
Тогда, если сущ. предел отношения
производных этих функ.
.
Тогда, если сущ. предел отношения
производных этих функ. 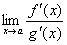 ,
то сущ. и предел отношения самих
функ. f(x)/g(x) при x→а, причем
,
то сущ. и предел отношения самих
функ. f(x)/g(x) при x→а, причем
|
|
Коротко правило Лопиталя можно сф ормулировать след. образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных. Теорема Лагранжа
Если функ. f(x) непрерывна на замкнутом отрезке [a, b], дифференцируема внутри него, то сущ.такая точка с Î (a, b), что выполняется равенство f(b)−f(a)=f'(c)·(b−a). Доказательство.Составим урав.хорды,проходящей через точки(a,f(a)),(b,f(b)) y=f(a)+Q·(x-a),где есть угловой коэффициент хорды.Рассмотрим разность ординат функ.и хорды F(x)=f(x)−f(a)−Q·(x−a). Очевидно, что функ. F(x) удовлетворяет всем условиям теоремы Ролля. Поэтому на интервале (a, b) найдётся такая точка с, для которой F ' (c) = 0. То естьF'(c)=f'(c)−Q=0.Откуда следует . И,наконец,f(b)−f(a)=f'(c)·(b−a).
