17)Матрицы

Матрицей А размера m на n наз.прямоугольная таблица из m строк и n столбцов,состоящая из чисел или иных матем.выражений .Квадратной матрицей n-го порядка наз.матрица размера n на n.Диагональной наз.квадратная матрица,у котрой все элементы вне главной диагонали равны 0.Единичной наз.диагональная матрица с единицами на главной диагонали.Нулевой наз.матрица,все элементы которой равны 0.

Операции над матрицами

Суммой матриц А= и B= одинакового размера наз.матрица С= того же размера.Свойства операции сложения матриц .Для любых матриц А,B,C одного размера выполняются равенства:1)A+B=B+A 2)(A+B)+C=A+(B+C)=A+B+C

Произведение матриц А= на число j наз.матрица B= того же размера,что и матрица А.Свойства операции умножения матрицы на число:1)j(

Свойства операции умножения1)(A B)C=A(BC)=ABC 2)(A+B)C=AC+BC 3)A(B+C)=AC+BC 4)AB

Транспонированной к матрице А= наз.матрица =( ) такая,что .Элемент строки матрицы назовём крайним,если он отличён от 0,а все элементы этой строки,находящиеся левее него,равны 0.Матрица наз.ступенчатой,если крайний элемент каждой строки находится правее крайнего элемента предыдущей строки

Диагональная матр., у кот. все элементы на главной диагонали равны 1, наз. единичной матрицей (Е).

18)Определители

Определитель 2-го порядка задаётся равенств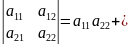ом: ).Опредилитель 2-го порядка есть сумма 2=2!слагаемых ,каждое из кот. представляет собой произведение 2-х сомножителей-элементов матрицы А,по одному из каждой строки и каждого столбца.Одно из слогаемых берется со знаком +,другое-со знаком -.

Определитель 3-го порядка задаётся равенством:

Определитель3-го порядка есть сумма 6=3! Слагаемых,каждое из которых представляет собой произведение 3-х сомножителей-элементов матрицы А,по одному из каждой строки и каждого столбца.Одна половина слагаемых берётся со знаком +,другая со знаком -.

19)Алгеброическим дополнением к элементу квадратной матрицы А= наз.произведение *

Определитель n-го порядка задаётся равенством: = .Указанная сумма состоит из n!слагаемых,каждое из которых представляет собой произведение

Сомножителей-элементов матрицы А,по одному из каждой строки и каждого столбца.Одна половина слагаемых берется со знаком +,другая мо знаком -.

20)Обратной матрицей к квадратной матрице А наз.такая матрица ,что 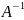*А=А* =Е .Присоединенной матрицей к квадратной матрице А= ,наз матрица = ,получ.транспонированием из матрицы,составленной из алгебраических дополнений

Если квадратеая матрица А-невырожденная,то .

Алгоритм нахождения:1)Вычислим определитель матрицы А,если опр.=0,то обратная матрица не сущ.2)Если опред.не равен 0,то обратная матрица сущ.Находим алгеброическое дополнение элементов матрицы А и составляем матрицу из них = 3)Транспонируем матрицу и получ.присоединённую матрицу 4)Находим обратную матрицу по формуле = 5)Осущ.проверку А* =

21) Пусть K - поле, , , . Если , то называется собственным числом матрицы A, а - собственным вектором матрицы A, отвечающим собственному числу .

22)Системы линейных уравнений.

Система m линейных алгебраических уравнений с n неизвестными в линейной алгебре — это система уравнений вида

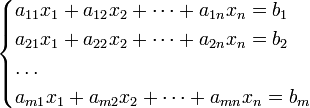
Здесь m — колич. Урав., а n — колич. неизвестных.

Система линейных урав. может быть представлена в матричной форме как:

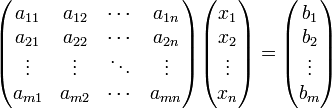
Правило Крамера.Если определитель матрицы А отличен от 0, то система имеет единственное решение определяемое из форм.X_i= где определитель полученный из определителя матрицы А с заменой i-того столбца столбцом свободных членов.