
- •1)Полярная система
- •5)Кривые второго порядка
- •11)Размерность и базис линейного пространства, координаты вектора
- •14.Пусть плоскость q проходит через точку м0 (x0 ,y0 ,z0 ) перпендикулярно вектору
- •15) Угол между плоскостями
- •17)Матрицы
- •18)Определители
- •23)Решение системы линейных уравнений матричным методом
- •25) Теорема Кронекера – Капелли
- •28)Экономическая интерпретация числа е
- •29)Функции и отображения их области опред. И знач.
- •32) Односторонний предел
- •33)Бесконечно малые величины и их св-ва
- •34)Непрерывность функции в точке.
- •35)Непрерывность сложной функции и обратной функции.
- •37)Определение Производной
- •39)Производные основных элементарных функций.
- •40 Дифференциал функции.
- •41. Производные и дифференциалы высших порядков
- •2)Теорема Ферма и Ролля.
- •44.Условия постоянства функции
- •45.Экстремумы функции
- •46.)Условие выпуклости и вогнутости функции. Точка перегиба.
- •47).Асимптоты.
- •48)Функ. Нескольких переменных
- •52)Первоообразная функции и неопределённый интеграл
- •53)Метод замены переменной
- •55)Интегрирование простейших рац. Дробей
- •56)Интегрирование рациональных дробей
- •57)Интегрирование тригонометрических функций
- •58)Определенный интеграл.
- •59.)Основные свойства определённого интеграла
- •61.)Применение определённого интеграла для вычисления площадей фигур, длин дуг плоских кривых и объёмов тел.
- •62.)Несобственные интегралы
- •66)Неоднородными дифференциальным урав. Второго порядка с постоянными коэффициентами наз. Уравнение вида , где p и q- постоянные, – функ., непрерывная на некотором множестве х.
- •68).Признаки сходимости рядов с положительными членами
1)Полярная система
Полярная
система
координат задаётся т.О,наз.полюсом,лучом
Ор,наз.полярной осью,и единичным вектором
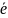 того же направления,что и луч Ор.
того же направления,что и луч Ор.
Положение
т.М на плоскости определяется двумя
числами :её расстоянием r
от полюса О и углом
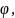 образованным
отрезком ОМ с полярной осью и отсчитываемым
в положительном направлении.
образованным
отрезком ОМ с полярной осью и отсчитываемым
в положительном направлении.

r
M(r, )
)
p
O
Числа
r
и
 наз.полярными координатами т.М: r
наз.полярным радиусом,
наз.полярными координатами т.М: r
наз.полярным радиусом,
Системы координат в пространстве: декартовы
Декартова система координат в пространстве определяется точкой и базисом из трех векторов. Точка O называется началом координат. Прямые, проведенные через начало координат в направлении базисных векторов, называются осями координат. В трехмерном пространстве они называются осями абсцисс, ординат и аппликат. Оси координат являются числовыми осями с началом в точке O , положительным направлением, совпадающим с направлением соответствующего базисного вектора, и единицей длины, равной длине этого вектора. Координатами точки M называются координаты вектора OM (радиус–вектора) (см. рис. 1). Если базис ортонормированный, то связанная с ним декартова система координат называется прямоугольной.
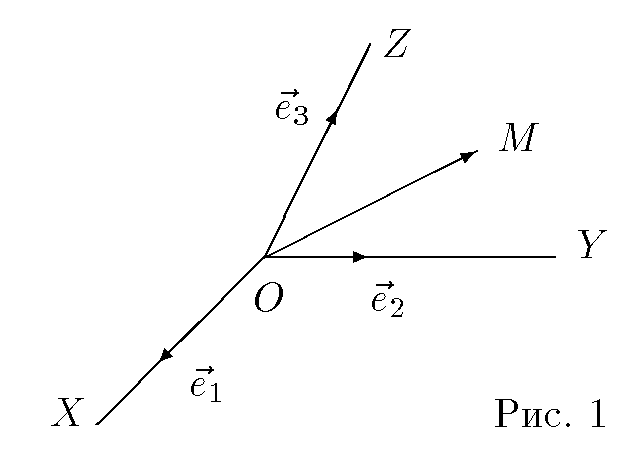
2)Общее ур.прямой: Ax +By+C=0 (A,B.C-постоянные коэффициенты,причём Аи В одновреммено не обращаются в 0
Ур.прямой с угловым коэффициентом имеет вид у=kx+b(k-угловой коэф.прямой,b-ордината точки пересечения прямой с осью Оу)
Нормальное
ур.прямой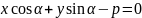 (р-длина
перпендикуляра,опущ. из начала координат
на прямую,
(р-длина
перпендикуляра,опущ. из начала координат
на прямую, -угол,кот.
этот перпендикуляр образует с полож.
направлением оси Ох
-угол,кот.
этот перпендикуляр образует с полож.
направлением оси Ох
3)Под углом между прямыми в плоскости понимают наименьший из двух смежных углов,образованными этими прямыми
Если
прямые
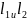 заданы урав.с угловыми коэф. У=
заданы урав.с угловыми коэф. У= x+
x+ и у=
и у=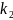 x+
x+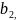 то угол
между ними выч. По фор.
то угол
между ними выч. По фор.
Tg
=
Условие параллельности прямых имеет вид
 ,
а условие их перпедикулярности
,
а условие их перпедикулярности
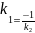
Если
прямые
заданы общими ур. x+
x+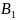 y+
y+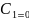 и
и
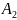 x+
x+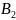 y+
y+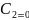 ,то
величина
угла между ними выч. по фор. tg
,то
величина
угла между ними выч. по фор. tg ,условие
их параллельности
,условие
их параллельности
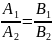
Для
нахождения общих точек прямых
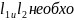 димо
решить систему ур.
димо
решить систему ур.
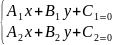
4)Расстоянием
d
от точки
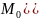 )
до прямой
)
до прямой
 x+
x+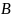 y+
y+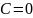 наз.длина перпендикуляра ,опущенного
из этой точки на прямую
наз.длина перпендикуляра ,опущенного
из этой точки на прямую
Расст.d
опред.по фор.d=
Расст.от
точки
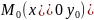 до прямой
выч. по форм.
до прямой
выч. по форм.
d=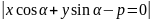
5)Кривые второго порядка
Линии,определяемые
алгебраическими ур.второй степени
относительно переменных х и у ,т.е ур.вида
А +2
Вху+С
+2
Вху+С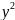 +2Dx+2Ey+F=0,наз.кривыми
второго порядка
+2Dx+2Ey+F=0,наз.кривыми
второго порядка
Окружностью наз.множество всех точек плоскости,удалённых от заданной т.А на одно и тоже расстояние R. т.А наз.центром,а R-радиусом окружности
Ур.окружности
имеет вид
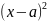 +
+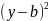 =
=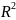 (каноническое
урав.окружности).Если а=0,b=0,то
ур.имеет вид
(каноническое
урав.окружности).Если а=0,b=0,то
ур.имеет вид
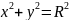
Эллипсом наз.множество всех точек плоскости,сумма расст. от каждой из кот. до двух данных точек,наз.фокусами,есть величина постоянная,большая,чем расст. между фокусами
Каноническое
ур.эллипса: =1,где
а-большая полуось,b-малая
полуось эллипса
=1,где
а-большая полуось,b-малая
полуось эллипса
Точки
А,В,С наз. вершинами эллипса,т.О-центром
эллипса,расстояние
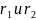 от произвольной точки М эллипса до его
фокусов наз.фокальными радиусами этой
точки
от произвольной точки М эллипса до его
фокусов наз.фокальными радиусами этой
точки
Эксцентриситетом
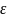 эллипса наз.отношение фокусного
расстояния 2с к большой оси 2а:
эллипса наз.отношение фокусного
расстояния 2с к большой оси 2а:

Фокальные
радиусы опред.формулами
 ,
,

Директрисами
эллипса наз.
параллельные
малой оси эллипса и отстоящие от неё
на расстоянии,равном
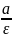 ,ур.директрис:x=
и x=
,ур.директрис:x=
и x=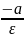
1)Если
а=b,то
ур.
=1
определяет окружность

2)ур.эллипса
с осями,параллельными координатным,имеет
вид
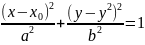
3)ур. t
t
Гиперболой наз.множество всех точек плоскости,модуль разности расстояний от каждой из которых до двух заданных точек,наз.фокусами,есть величина постоянная,меньшая,чем расстояние между фокусами
Каноническое ур.гиперболы: =1,где а –действительная,b-мнимая полуось гиперболы
Точки Аи В наз.вершинами гиперболы,т.О-центром гиперболы,расстояния от произвольной т.М гиперболы до её фокусов наз.фокальными радиусами этой точки
Число
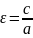 ,наз.эксцентриситетом
гиперболы
,наз.эксцентриситетом
гиперболы
Прямоугольник,центр
которого совпадает с т.О,а стороны равны
и параллельны осям гиперболы наз.основным
прямоугольником гиперболы.Диагонали
основного прямоугольника гиперболы
лежат на двух прямых,наз.асимптотами
гиперболы,они определяются ур.у= x
x
Две прямые параллельные мнимой оси гиперболы и отстоящие от неё на расстоянии,равном ,наз.директрисами гиперболы.их ур. x= и x=
Параболой наз.множество всех точек плоскости,каждая из которых равноудалена от заданной точки,наз.фокусом и заданной прямой ,наз.директрисой
Каноническое ур.параболы имеет вид
=2рх,где
число р>0,равное расстоянию от фокуса
F
до директрисы l,наз.
Параметром параболы.Координаты фокуса
F( )Точка
О(0,0)наз. Вершиной параболы,длина r
отрезка FM-фокальный
радиус т.М,ось Ох-ось симметрии параболы
)Точка
О(0,0)наз. Вершиной параболы,длина r
отрезка FM-фокальный
радиус т.М,ось Ох-ось симметрии параболы
Ур.директрисы
l
параболы имеет вид х=-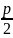 ,фокальный
радиус выч.по фор.r=x+
,фокальный
радиус выч.по фор.r=x+
6)Сложение векторов. Так как векторы - это направленные отрезки, то их сложение может быть выполнено геометрически. (Алгебраическое сложение векторов изложено ниже, в пункте «Единичные ортогональные векторы»). Предположим, что a = AB and b = CD ,
тогда вектор a + b = AB + CD
есть результат выполнения двух операций
a) параллельного переноса одногоиз векторов таким образом, чтобы его начальная точка совпала с конечной точкой второго вектора;
б) геометрического сложения, т.е. построения результирующего вектора, идущего от начальной точки неподвижного вектора к конечной точке перенесённого вектора.
Законы умножения вектора на число.
I. 1 · a = a , 0 · a = 0 , m · 0 = 0 , ( –1 ) · a = – a .
II. m a = a m , | m a | = | m | · | a | .
III. m ( n a ) = ( m n ) a . ( С о ч е т а т е л ь н ы й закон умножения на число ).
IV. ( m + n ) a = m a + n a , ( Р а с п р е д е л и т е л ь н ы й
m ( a + b ) = m a + m b . закон умножения на число ).
Законы сложения.
I. a + b = b + a ( П е р е м е с т и т е л ь н ы й закон ).
II. ( a + b ) + c = a + ( b + c ) ( С о ч е т а т е л ь н ы й закон ).
III. a + 0 = a .
IV. a + (– a ) = 0 .
7)Скалярным
произведением двух ненулевых векторов
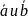 наз.число, равное произведению длин
этих векторов на косинус угла
между ними.
наз.число, равное произведению длин
этих векторов на косинус угла
между ними.
 =
=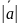 *
*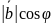
Свойства скалярного произведения:
1.
 –
переместительное свойство;
–
переместительное свойство;
2.
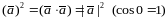 – скалярный квадрат вектора;
– скалярный квадрат вектора;
3.
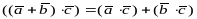 – распределительное свойство;
– распределительное свойство;
4. – сочетательное свойство относительно
числового множителя.
– сочетательное свойство относительно
числового множителя.
8)Ось – это прямая, кот. придается какое–то направление.dектор с бесконечно большим модулем. Ось обозначается какой-либо буквой: X , Y , Z , s , t … Обычно на оси выбирается (произвольно) точка, кот. наз. началом отсчета и, как правило, обозначается буквой О. От этой точки отсчитываются расстояния до др/интересующих нас точек. Проекция точки на ось - это основание перпендикуляра, опущенного из этой точки на данную ось (рис. 8). То есть, проекцией точки на ось является точка.

Рис. 8
Координата точки - это число, абсолютная величина кот. равна длине отрезка оси (в выбранном масштабе), заключённого между началом оси и проекцией точки на эту ось. Это число берется со знаком плюс, если проекция точки располагается в направлении оси от ее начала и со знаком минус, если в противоположном направлении. Скалярная проекция вектора на ось - это число, абсолютная величина кот. равна длине отрезка оси (в выбранном масштабе), заключённого между проекциями точки начала и точки конца вектора. Обычно вместо выражения скалярная проекция говорят просто – проекция, то есть слово скалярная опускают. Проекция обозначается той же буквой, что и проектируемый вектор (в обычном, нежирном написании), с нижним (как правило) индексом названия оси, на которую этот вектор проектируется. Например, если на ось Х проектируется вектор а, то его проекция обозначается аx. При проектировании этого же вектора на другую ось, скажем, ось Y , его проекция будет обозначаться аy (рис. 9).
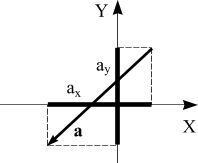
Рис. 9
Чтобы вычислить проекцию вектора на ось (например, ось X) надо из координаты точки его конца вычесть координату точки начала, то есть
аx = хк − xн.
Надо помнить: проекция вектора на ось - это число! Причем, проекция может быть положительной, если величина хк больше величины хн, отрицательной, если величина хк меньше величины хн и равной нулю, если хк равно хн (рис. 10).
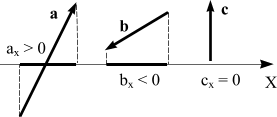
Рис. 10
Проекцию вектора на ось можно также найти, зная модуль вектора и угол, который он составляет с этой осью. Из рисунка 11 видно, что аx = а Cos α то есть, проекция вектора на ось равна произведению модуля вектора на косинус угла между направлением оси и направлением вектора. Если угол острый, то Cos α > 0 и аx > 0, а, если тупой, то косинус тупого угла отрицателен, и проекция вектора на ось тоже будет отрицательна.
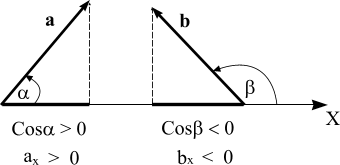
Рис. 11
Углы, отсчитываемые от оси против хода часовой стрелки, принято считать положительными, а по ходу - отрицательными. Однако, поскольку косинус – функция четная, то есть, Cos α = Cos (− α), то при вычислении проекций углы можно отсчитывать как по ходу часовой стрелки, так и против. При решении задач часто будут использоваться следующие свойства проекций: если а = b + c +…+ d , то аx = bx + cx +…+ dx (аналогично на другие оси),если a = mb, то аx = mbx (аналогично на другие оси).
Чтобы найти проекцию вектора на ось надо модуль этого вектора умножить на косинус угла между направлением оси и направлением вектора.
10.
)Линейным
пространством пространство
![]() над
полем
над
полем
![]() —
это непустое
множество
—
это непустое
множество
![]() ,
на котором введены операции
,
на котором введены операции
сложения, то есть каждой паре элементов множества
 ставится
в соответствие элемент того же множества,
обозначаемый
ставится
в соответствие элемент того же множества,
обозначаемый
 и
иумножения на скаляр (то есть элемент поля ), то есть любому элементу
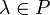 и
любому элементу
и
любому элементу
 ставится
в соответствие единственный элемент
из
,
обозначаемый
ставится
в соответствие единственный элемент
из
,
обозначаемый
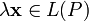 .
.
При этом на операции накладываются следующие условия:
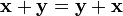 ,
для любых
(коммутативность
сложения);
,
для любых
(коммутативность
сложения);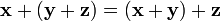 ,
для любых
,
для любых
 (ассоциативность
сложения);
(ассоциативность
сложения);существует такой элемент
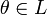 ,
что
,
что
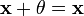 для
любого
(существование
нейтрального элемента относительно
сложения),
в частности
не
пусто;
для
любого
(существование
нейтрального элемента относительно
сложения),
в частности
не
пусто;для любого существует такой элемент
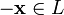 ,
что
,
что
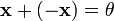 (существование
противоположного элемента относительно
сложения).
(существование
противоположного элемента относительно
сложения).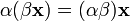 (ассоциативность
умножения на скаляр);
(ассоциативность
умножения на скаляр);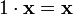 (унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор).
(унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор). (дистрибутивность
умножения на вектор относительно
сложения скаляров);
(дистрибутивность
умножения на вектор относительно
сложения скаляров); (дистрибутивность
умножения на скаляр относительно
сложения векторов).
(дистрибутивность
умножения на скаляр относительно
сложения векторов).
Элементы множества называют векторами, а элементы поля — скалярами.
Система векторов e1,e2, ..., ek линейного пространства L наз. линейно независимой системой, если равенство С1·e1+С2·e2+ ...+Сk· ek = 0 возможно только когда все коэффициенты С1, С2, ..., Сk равны нулю.
Здесь 0 — нулевой вектор линейного пространства L, С1, С2, ..., Сk — числовые коэффициенты. Если система векторов e1,e2, ..., ek линейного пространства L не явл. линейно независимой системой, то она наз. линейно зависимой системой векторов.Если векторы скалярное произведение кот. равно 0,наз.ортогональными
Критерий линейной зависимости векторов
Для
того чтобы векторы
![]() (r
> 1)
были линейно зависимы, необходимо и
достаточно, чтобы хотя бы один из этих
векторов являлся линейной комбинацией
остальных.
(r
> 1)
были линейно зависимы, необходимо и
достаточно, чтобы хотя бы один из этих
векторов являлся линейной комбинацией
остальных.
