23. Жесткие задачи: понятие о жестких задачах, жесткие системы дифференциальных уравнений. Методы их решения.

Все попытки увеличить шаг и тем самым уменьшить время решения задачи приводят лишь к катастрофически большому росту погрешности. Обладающие этим св-вом задачи получили название жестких.

Рассм. зад. Коши для систем лин.дифф. ур-ий с постоянными коэф.

Все собственные числа матрицы А имеют отрицательные вещественные части. Решение имеет вид

погрешность :

Для медленной компоненты решения временной постоянной является , а для жесткой компоненты погрешности . Их отношение определяет степень жесткости задачи.

Числом жесткости называется величина: 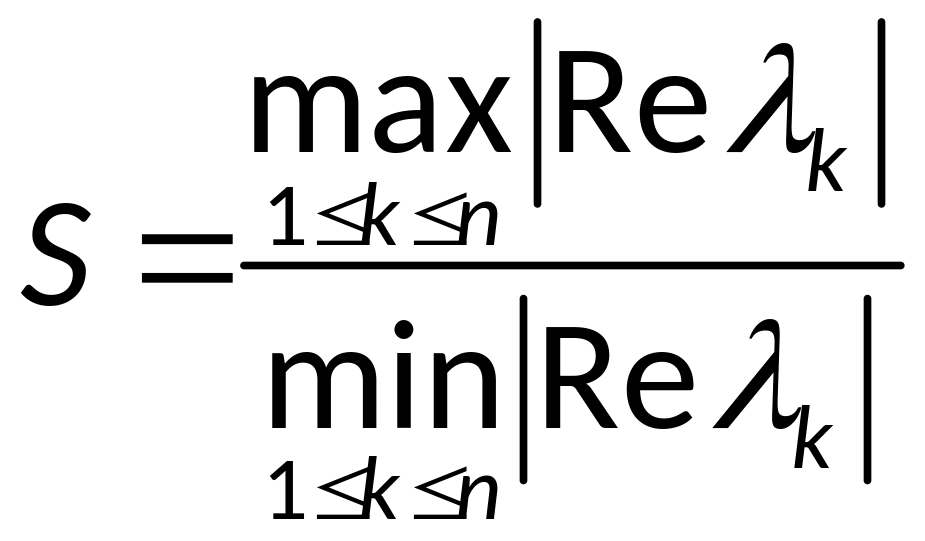,систему ур-ий назовем жесткой, если для нее

Для решения жестких задач предпочтительны А-устойчивые методы, т.к. они не накладывают никаких ограничений на шаг,но класс таких методов весьма узок. Можно заменить менее ограничительным требованием наличия у метода А( )-устойчивости : если область абс.устойчивости метода включает угол . Среди неявных линейных многошаговых методов имеются А( )-устойчивые методы высокого порядка точности. Важный класс таких методов (формул дифференцирования назад) относится к так называемым чисто неявным методам. 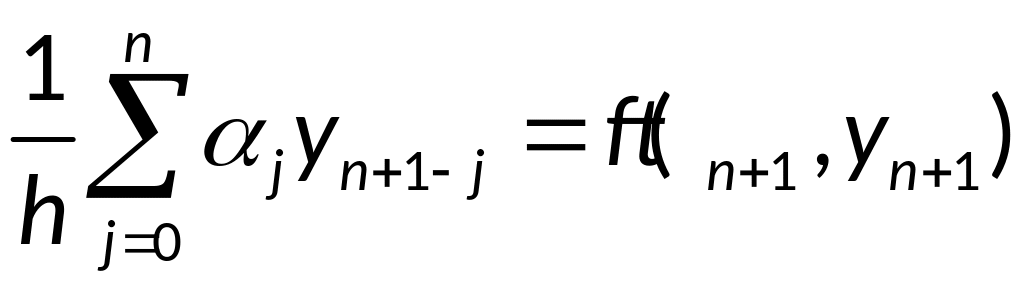(Например неявный метод Эйлера или алгоритм Гира).

24. Постановка двухточечной краевой задачи. Основные теоремы (без доказательств) о разрешимости и устойчивости дифференциальной задачи.

Двухточечная краевая задача- это задача отыскания решения обыкновенного дифференциального уравнения или системы обыкновенных дифференциальных уравнений на отрезке , в которой дополнительные условия накладываются в двух точках a и b- краях отрезка.

Стационарное уравнение теплопр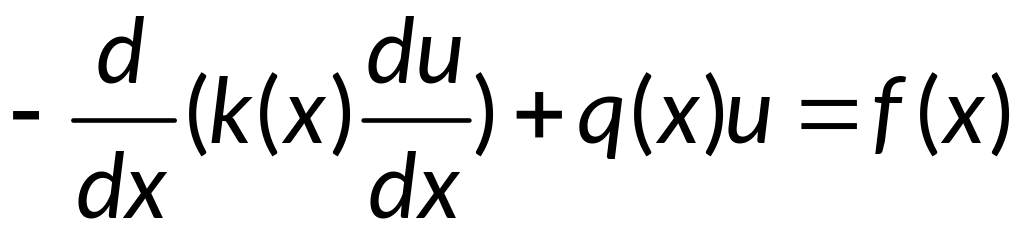оводности : (1), где k(x)- коэф. теплопроводности, - 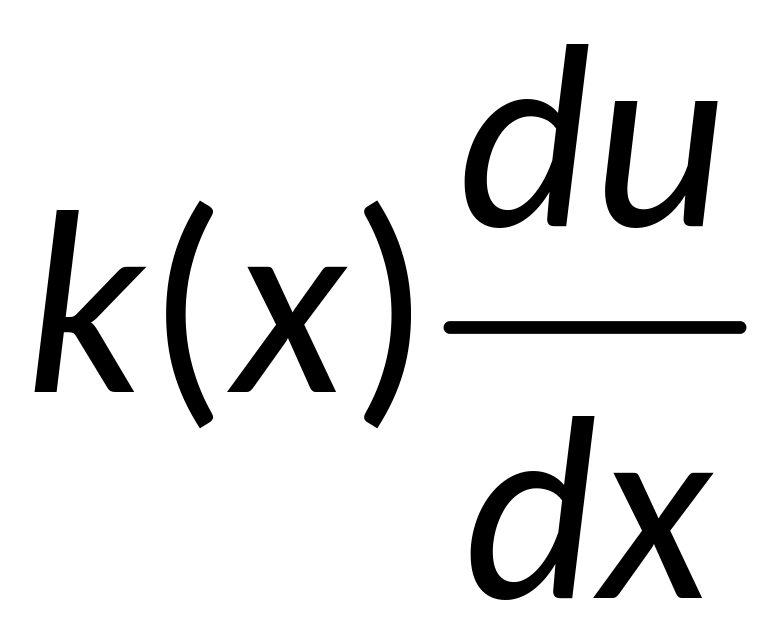- плотность потока тепла, q(x)- коэф. теплоотдачи, f(x)- плотность источников тепла.

Граничные условия первого рода: - физич.интерп.: на торцах стержня поддерживаются фиксированные значения температуры.

Граничные условия второго рода: , -задана плотность потока тепла на торцах стержня.

Теорема1 : Решение краевой задачи существует и единственно.

Теорема2 : Пусть -дважды непрерывно дифференцируемая на отрезке функция, удовлетворяющая неравенствам . Тогда . Где

Теорема3(теорема сравнения) : Пусть , -дважды непрерывно дифференцируемые на отрезке функции, удовлетворяющие неравенствам , . Тогда .

Теорема об устойчивости: Пусть - решение краевой задачи (1)(с гранич. условиями первого рода), а -решение краевой задачи

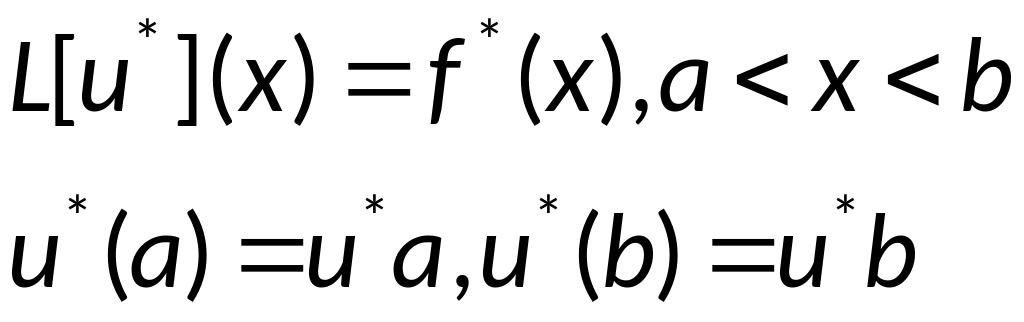( -приближенно заданные)

Справедлива оценка: ,где

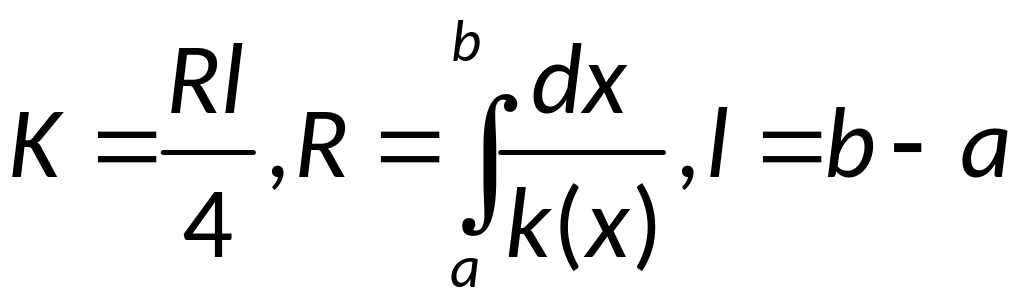
25. Дискретная двухточечная краевая задача. Теорема о существовании решения разностной схемы.

Двухточечная краевая задача- это задача отыскания решения обыкновенного дифференциального уравнения или системы обыкновенных дифференциальных уравнений на отрезке , в которой дополнительные условия накладываются в двух точках a и b- краях отрезка.

Смысл построения разностной схемы заключается в дискретизации краевой задачи, т.е. замене области непрерывного изменения аргумента сеткой- конечным набором точек.

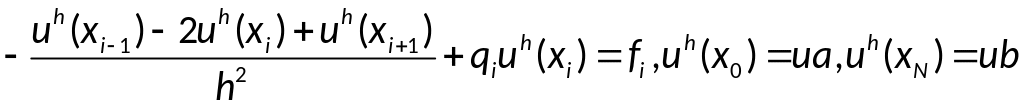- в результате дифференциальное уравнение оказалось его дискретным аналогом – разностным уравнением.

Обозначим : 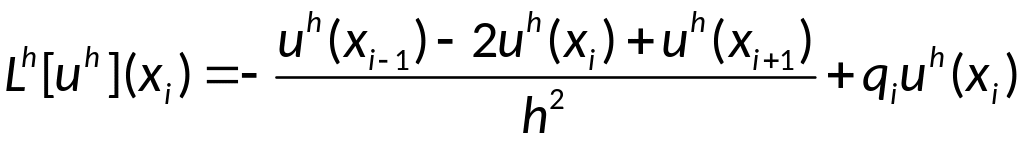,запишем систему сеточных ур-ий в след виде:

(1)

(2) эту дискретную задачу принято называть разностной схемой.

Теорема о существовании решения разностной схемы: Решение разностной схемы существует и единственно. =))