14. Численные методы решения задачи Коши: методы Рунге–Кутты. Идея построения расчетных формул. Метод Рунге-Кутты 4-го порядка точности.

дана задача Коши. 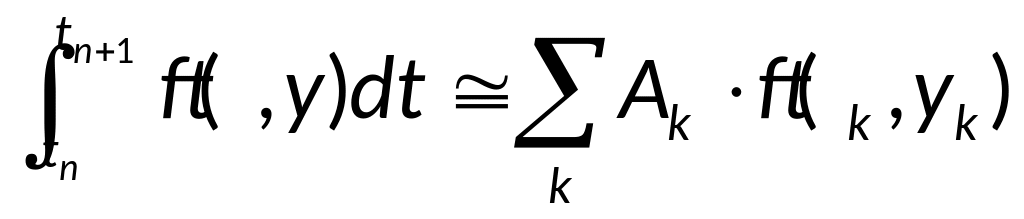1.Формула левых прям. - явный метод Эйлера( одношаговый). E(h)=ch – 1-го порядка точности 2.Формула правых прям. Неявный метод Эйлера. E(h)=ch – 1го пор.точн. 3.Формула центр. Прям. E=c Усоверш. Метод Эйлера 4.Формула трапеций .- метод Эйлера-Коши, E=c 5.Формула Симпсона

, , , , , , Метод Рунге-Кутты 4-го порядка точности. Идея:что мы интегрируем левую и правую часть задачи коши,левую мы заменяем разностной производной и считаем интеграл,а правую интегрируем с помощью какой-нибудь формулы и вот в зависимости от формулы интегрирования получаем расчетные формулы разных методов Теорема: пусть правая часть диффер. Ур-ния удовлетвор. условию Тогда всякий явный m-этапный метод Рунге-Кутты устойчив на конечном отрезке

Общая явная p-этапная схема Рунге-Кутты по опред-ию имеет вид: s=2...p Коэффиц. , , определяются (как и в предыдущем пункте) так, чтобы функция Φ наилучшим образом аппроксимировала функцию. Подробнее эта процедура выглядит так. Вычисляются частные производные функции Φ порядков 0, ..., p – 1 по h при h = 0 и приравниваются к производным точного решения. При этом для методов высокого порядка (p ≥ 3) обычно предполагаются выполненными дополнительные условия вида которые сильно упрощают как решение, так и исследование системы уравнений на коэффициенты искомых схем.

16. Явные одношаговые методы. Локальная и глобальная погрешности. Оценка погрешности по правилу Рунге.

В основе построения конкретного численного метода лежит тот или иной способ замены дифф.ур-ния y’=f(t,y) его дискретным аналогом – ур-ем вида (1). При k=1 уравнение упрощается и принимает вид (2)- этот метод называется одношаговым. Вычисление значения осущест-ся здесь с использованием только одного предыдущего значения .Поэтому одношаговые методы часто зовут самостартующими. В случае когда входящая в уравнение (1) функция Ф не зависит от , вычисление значения не вызывает затруднений и осуществляется по явной формуле ,соответствующие методы называют явными. Пусть - значение, найдено из (2), в кот. вместо подставлено точное значение решения дифф. ур-ния в точке t= . Тогда разность называется локальной погрешностью метода. - погрешность, кот. допускают за один шаг метод, стартовавший с точного решения. - погрешность аппроксимации. Пусть y(t) – решение задачи Коши. Назовем глобальной погрешностью численного метода сеточную ф-цию со значениями в узлах . В качестве меры абсолютно погрешности метода примем величину E(h)= Численный метод задачи Коши называется сходящимся, если для него E(h)->0 при h->0. Принято говорить, что метод сходится с Р-м порядком точности, если для погрешности справедлива оценка E(h) ,p>0. Оценка погрешности по правилу Рунге: Уточнение по Рунге: