
- •Численное интегрирование: вывод формулы прямоугольников и оценки погрешности.
- •Численное интегрирование: вывод формулы трапеций и оценки погрешности.
- •Численное интегрирование: формула Симпсона и оценка погрешности.
- •Правило Рунге оценки погрешностей. Уточнение по Рунге.
- •Численное дифференцирование. Вычисление первой и второй производной, оценки погрешности.
- •Задача Коши для дифференциального уравнения первого порядка: постановка задачи, её разрешимость, устойчивость на конечном отрезке.
- •Задача Коши для дифференциального уравнения первого порядка: устойчивость по правой части и на неограниченном промежутке.
- •Численные методы решения задачи Коши. Основные понятия и определения: дискретная задача Коши, явные и неявные методы, устойчивость, аппроксимация, сходимость.
- •Численные методы решения задачи Коши. Метод разложения в ряд Тейлора.
- •Численные методы решения задачи Коши. Метод Эйлера, его геометрическая интерпретация, оценка погрешности метода Эйлера.
- •13.Численные методы решения задачи Коши: модификации метода Эйлера второго порядка точности, геометрическая интерпретация, оценка погрешности методов.
- •14. Численные методы решения задачи Коши: методы Рунге–Кутты. Идея построения расчетных формул. Метод Рунге-Кутты 4-го порядка точности.
- •16. Явные одношаговые методы. Локальная и глобальная погрешности. Оценка погрешности по правилу Рунге.
- •17. Аппроксимация, устойчивость и сходимость явных методов решения задачи Коши.
- •15. Сходимость метода Эйлера.
- •18. Решение задачи Коши для систем дифференциальных уравнений.
- •19.Решение задачи Коши для уравнения m-го порядка.
- •20. Многошаговые методы. Вывод формул явного метода Адамса-Башфорта. Порядок аппроксимации метода.
- •21. Многошаговые методы. Вывод формул неявного метода Адамса-Моултона. Порядок аппроксимации метода.
- •22. Устойчивость численных методов. Понятие нуль-устойчивости.
- •23. Жесткие задачи: понятие о жестких задачах, жесткие системы дифференциальных уравнений. Методы их решения.
- •24. Постановка двухточечной краевой задачи. Основные теоремы (без доказательств) о разрешимости и устойчивости дифференциальной задачи.
- •25. Дискретная двухточечная краевая задача. Теорема о существовании решения разностной схемы.
- •26. Дискретная двухточечная краевая задача. Априорная оценка решения разностной схемы (без доказательства).
- •27. Дискретная двухточечная краевая задача. Устойчивость разностной схемы.
- •28. Дискретная двухточечная краевая задача. Аппроксимация и сходимость разностной схемы.
- •29. Решение сеточных уравнений методом прогонки. Правило Рунге оценки погрешности.
- •30. Применение метода конечных разностей при решении двухточечной краевой задачи в случае переменного коэффициента теплопроводности.
- •31. Метод баланса построения разностных схем для решения двухточечной краевой задачи.
- •32. Метод конечных разностей решения первой начально-краевой задачи для одномерного уравнения теплопроводности: построение явной схемы и оценка погрешности.
- •33. Метод конечных разностей решения первой начально-краевой задачи для одномерного уравнения теплопроводности: условная устойчивость явной схемы.
- •34. Метод конечных разностей решения первой начально-краевой задачи для одномерного уравнения теплопроводности: неявная схема, абсолютная устойчивость неявной схемы.
- •35.Метод переменных направлений решения двумерной начально-краевой задачи для уравнений теплопроводности.
- •40. Метод конечных разностей решения задачи Дирихле для уравнения Пуассона. Итерационные методы решения сеточных уравнений: метод Зейделя.
Численные методы решения задачи Коши. Метод разложения в ряд Тейлора.
Один из наиболее
простых для понимания подходов к решению
задачи Коши основан на использовании
формулы Тейлора:

Отбрасывая остаточный член, получаем приближённое равенство
 .
.
Если значение
решения y
в точке t
известно, то в силу равенства
![]() значение производной
значение производной
![]() также можно считать известным.
также можно считать известным.
Найдём вторую
производную:
![]() .
.
Использование
приближённой формулы приводит к явному
одношаговому методу:
 .
.
Численные методы решения задачи Коши. Метод Эйлера, его геометрическая интерпретация, оценка погрешности метода Эйлера.
![]() - точное решение
- точное решение
![]() - приближённое
решение
- приближённое
решение
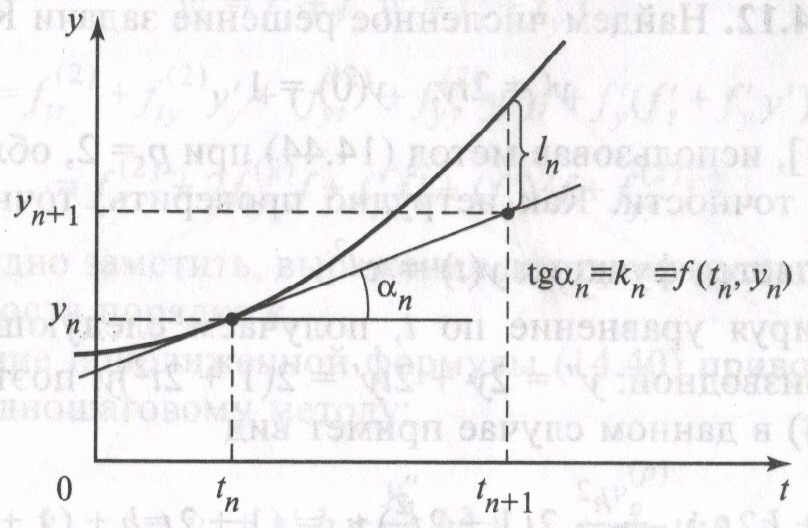
Геометрическая
интерпретация одного шага метода Эйлера
заключается в аппроксимации решения
на отрезке
![]() касательной
касательной
![]() - уравнение касательной.
- уравнение касательной.
![]()
![]() - расчётная формула
метода Эйлера.
- расчётная формула
метода Эйлера.
Метод Эйлера является устойчивым на конечном отрезке.
Погрешность
аппроксимации

Постановка задачи приближённого решения задачи Коши:
Требуется найти
функцию
![]() ,
,
![]()
![]() ,
- приближённое решение задачи, полученное
аналитическим методом.
,
- приближённое решение задачи, полученное
аналитическим методом.
Оценим погрешность аппроксимации метода Эйлера:

 ,
,
![]()
 ,
,
![]() - порядок аппроксимации первый.
- порядок аппроксимации первый.
13.Численные методы решения задачи Коши: модификации метода Эйлера второго порядка точности, геометрическая интерпретация, оценка погрешности методов.
О

 дин
шаг метода Эйлера приводит к значительной
величине локальной погрешности. Надо
бы ее уменьшить. Пусть y(t)
– решение дифф. ур-ния y’(t)=f(t,y(t))
, удовлетворяющее условию
дин
шаг метода Эйлера приводит к значительной
величине локальной погрешности. Надо
бы ее уменьшить. Пусть y(t)
– решение дифф. ур-ния y’(t)=f(t,y(t))
, удовлетворяющее условию![]() ,
далее пусть
,
далее пусть
![]() (1)
– угловой коэффиц. секущей, проходящей
через точки
(1)
– угловой коэффиц. секущей, проходящей
через точки
![]() и
и
![]() графика
ф-ции y(t)(рис
№1). Ясно,
что «метод», состоящий в вычислении по
формуле
графика
ф-ции y(t)(рис
№1). Ясно,
что «метод», состоящий в вычислении по
формуле
![]() (2) имеет нулевую локальную погрешность.
Надо научиться вычислять
(2) имеет нулевую локальную погрешность.
Надо научиться вычислять
![]() .
Интегрируя обе части уравнения
y’(t)=f(t,y(t))
по t
от
до
.
Интегрируя обе части уравнения
y’(t)=f(t,y(t))
по t
от
до
![]() и используя формулу Ньютона –Лейбница
и используя формулу Ньютона –Лейбница
![]() ,приходим
к равенству
,приходим
к равенству
![]() Из равенств (1) и (3) следует, что
Из равенств (1) и (3) следует, что
![]() (4)
Применение для приближенного вычисления
интеграла, стоящего в правой части
выражение (2), формулы левых прямоуг-ков
(4)
Применение для приближенного вычисления
интеграла, стоящего в правой части
выражение (2), формулы левых прямоуг-ков
![]() немедленно приводит от (2) к методу
Эйлера. Известно, что больший пор. точн.
имеет фор-ла трапец.
немедленно приводит от (2) к методу
Эйлера. Известно, что больший пор. точн.
имеет фор-ла трапец.
![]() Прямое
ее применение к вычислению
приводит к правилу трапеции:
Прямое
ее применение к вычислению
приводит к правилу трапеции:
![]() (5) Этот метод имеет 2ой порядок точности,
но явл. неявным. Построим на основе
правила трапеций явный метод. Для этого
подставим в правую часть формулу (5)
значение
,
полученное методом Эйлера. В результате
получим метод
(5) Этот метод имеет 2ой порядок точности,
но явл. неявным. Построим на основе
правила трапеций явный метод. Для этого
подставим в правую часть формулу (5)
значение
,
полученное методом Эйлера. В результате
получим метод
![]() (6) , который называется
методом
Эйлера –Коши(Хьюна).Геометрич.
Илл-ция кот. на рисунке № 2. Вычисления
разбивают на два этапа. На первом(этап
прогноза) в соответствии с методом
Эйлера
(6) , который называется
методом
Эйлера –Коши(Хьюна).Геометрич.
Илл-ция кот. на рисунке № 2. Вычисления
разбивают на два этапа. На первом(этап
прогноза) в соответствии с методом
Эйлера
![]()
![]() вычисляют
грубое приближение к значению
вычисляют
грубое приближение к значению
![]() .
В точке
.
В точке
![]() определяют
угловой коэффиц.
определяют
угловой коэффиц.
![]() .
На 2ом этапе (коррекции) вычисляют
усредненное значение углового коэффиц.
.
На 2ом этапе (коррекции) вычисляют
усредненное значение углового коэффиц.
![]() . Уточненное значение
находят по формуле
,
что соответствует шагу по прямой,
проходящей через точку
. Уточненное значение
находят по формуле
,
что соответствует шагу по прямой,
проходящей через точку
![]() и имеющий угловой коэффиц , равный
.
Метод (6), рассматривают как мод-кацию
метода Эйлера, кот. имеет 2й порядок
точности. Еще одну модификацию второго
порядка точности можно получить с
помощью формулы прямоуг-ков(центр.)
и имеющий угловой коэффиц , равный
.
Метод (6), рассматривают как мод-кацию
метода Эйлера, кот. имеет 2й порядок
точности. Еще одну модификацию второго
порядка точности можно получить с
помощью формулы прямоуг-ков(центр.)
![]() ,
,
![]() если для приближенного вычисления
значения
если для приближенного вычисления
значения
![]() .
В результате получим расчетные формулы
.
В результате получим расчетные формулы
![]()
![]() усовершенствованного
метода Эйлера.
усовершенствованного
метода Эйлера.
