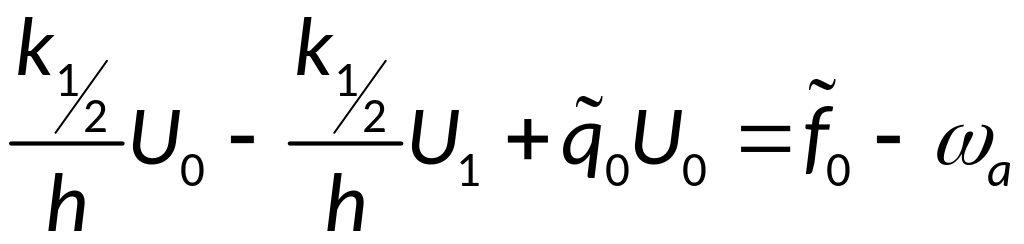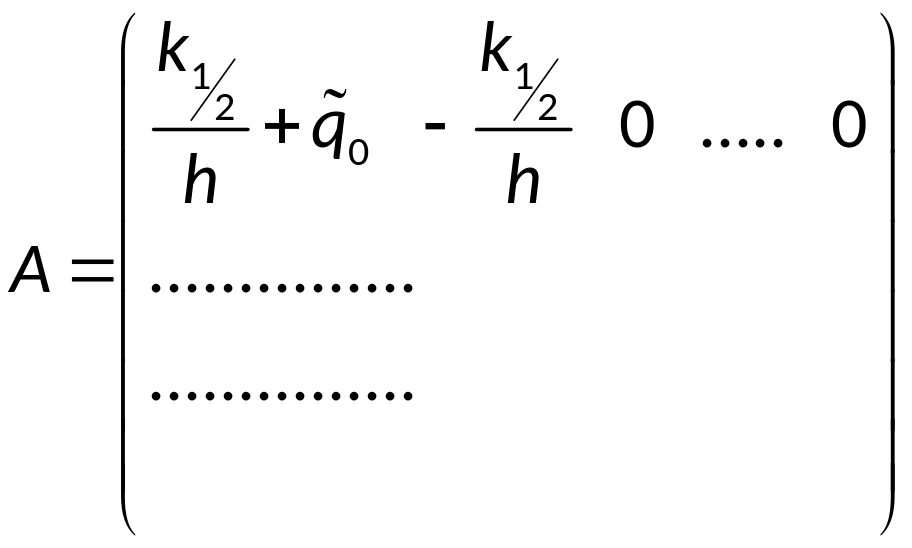- •Численное интегрирование: вывод формулы прямоугольников и оценки погрешности.
- •Численное интегрирование: вывод формулы трапеций и оценки погрешности.
- •Численное интегрирование: формула Симпсона и оценка погрешности.
- •Правило Рунге оценки погрешностей. Уточнение по Рунге.
- •Численное дифференцирование. Вычисление первой и второй производной, оценки погрешности.
- •Задача Коши для дифференциального уравнения первого порядка: постановка задачи, её разрешимость, устойчивость на конечном отрезке.
- •Задача Коши для дифференциального уравнения первого порядка: устойчивость по правой части и на неограниченном промежутке.
- •Численные методы решения задачи Коши. Основные понятия и определения: дискретная задача Коши, явные и неявные методы, устойчивость, аппроксимация, сходимость.
- •Численные методы решения задачи Коши. Метод разложения в ряд Тейлора.
- •Численные методы решения задачи Коши. Метод Эйлера, его геометрическая интерпретация, оценка погрешности метода Эйлера.
- •13.Численные методы решения задачи Коши: модификации метода Эйлера второго порядка точности, геометрическая интерпретация, оценка погрешности методов.
- •14. Численные методы решения задачи Коши: методы Рунге–Кутты. Идея построения расчетных формул. Метод Рунге-Кутты 4-го порядка точности.
- •16. Явные одношаговые методы. Локальная и глобальная погрешности. Оценка погрешности по правилу Рунге.
- •17. Аппроксимация, устойчивость и сходимость явных методов решения задачи Коши.
- •15. Сходимость метода Эйлера.
- •18. Решение задачи Коши для систем дифференциальных уравнений.
- •19.Решение задачи Коши для уравнения m-го порядка.
- •20. Многошаговые методы. Вывод формул явного метода Адамса-Башфорта. Порядок аппроксимации метода.
- •21. Многошаговые методы. Вывод формул неявного метода Адамса-Моултона. Порядок аппроксимации метода.
- •22. Устойчивость численных методов. Понятие нуль-устойчивости.
- •23. Жесткие задачи: понятие о жестких задачах, жесткие системы дифференциальных уравнений. Методы их решения.
- •24. Постановка двухточечной краевой задачи. Основные теоремы (без доказательств) о разрешимости и устойчивости дифференциальной задачи.
- •25. Дискретная двухточечная краевая задача. Теорема о существовании решения разностной схемы.
- •26. Дискретная двухточечная краевая задача. Априорная оценка решения разностной схемы (без доказательства).
- •27. Дискретная двухточечная краевая задача. Устойчивость разностной схемы.
- •28. Дискретная двухточечная краевая задача. Аппроксимация и сходимость разностной схемы.
- •29. Решение сеточных уравнений методом прогонки. Правило Рунге оценки погрешности.
- •30. Применение метода конечных разностей при решении двухточечной краевой задачи в случае переменного коэффициента теплопроводности.
- •31. Метод баланса построения разностных схем для решения двухточечной краевой задачи.
- •32. Метод конечных разностей решения первой начально-краевой задачи для одномерного уравнения теплопроводности: построение явной схемы и оценка погрешности.
- •33. Метод конечных разностей решения первой начально-краевой задачи для одномерного уравнения теплопроводности: условная устойчивость явной схемы.
- •34. Метод конечных разностей решения первой начально-краевой задачи для одномерного уравнения теплопроводности: неявная схема, абсолютная устойчивость неявной схемы.
- •35.Метод переменных направлений решения двумерной начально-краевой задачи для уравнений теплопроводности.
- •40. Метод конечных разностей решения задачи Дирихле для уравнения Пуассона. Итерационные методы решения сеточных уравнений: метод Зейделя.
29. Решение сеточных уравнений методом прогонки. Правило Рунге оценки погрешности.
Метод конечных разностей(или метод сеток): Область непрерывного изменения аргумента заменяют конечным множеством узлов, называемым сеткой. Вместо функций непрерывного аргумента рассматривают функции, определенные только в узлах сетки,-сеточные функции. Производные, которые входят в дифференциальное уравнение и краевые условия, заменяют их разностными аналогами. В результате краевую задачу заменяют дискретной краевой задачей(разностной схемой). Примем K(x)=1, тогда краевая задача:
![]()
Метод прогонки:
Прежде всего, нужно
построить сетку(равномерную, с постоянным
шагом
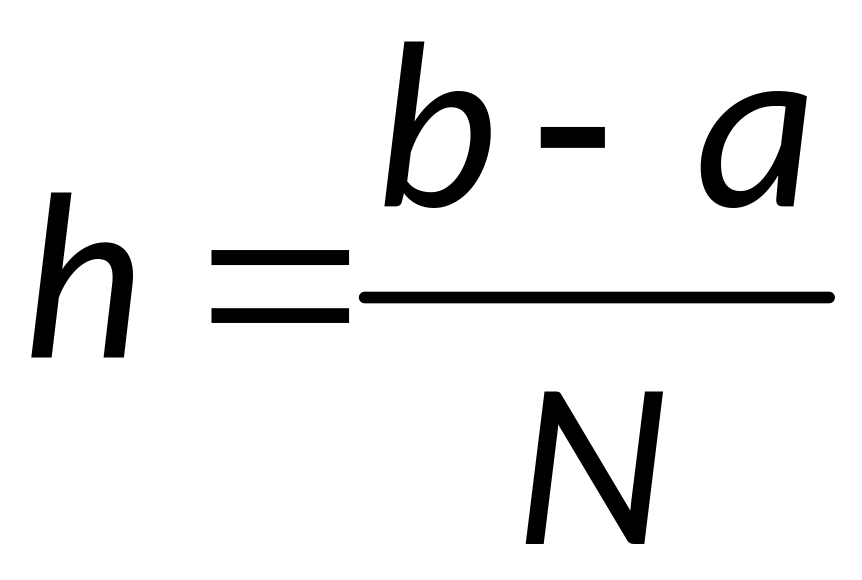 )
и ввести сеточные функции(
)
и ввести сеточные функции(![]() ),
затем построить разностную схему:
),
затем построить разностную схему:
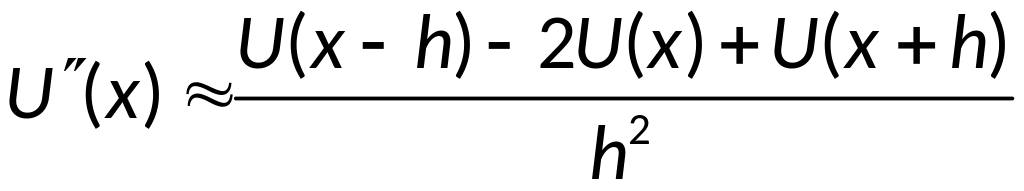 ,
с погрешностью
,
с погрешностью
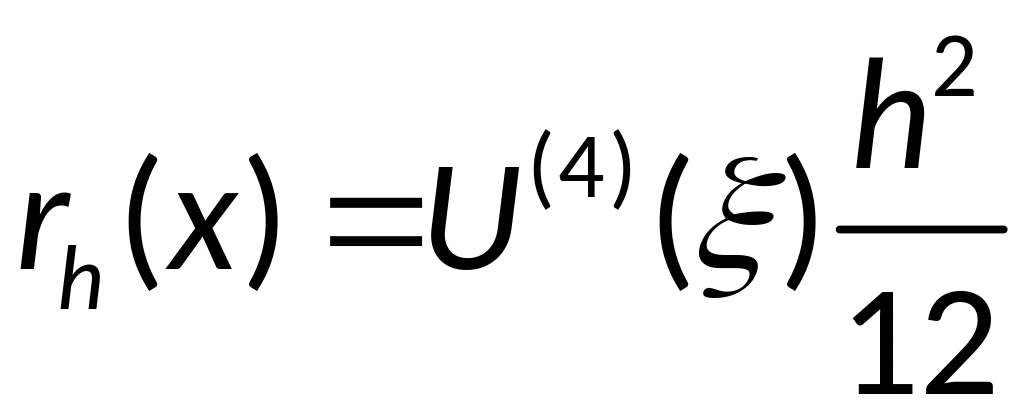
Заменим в каждом из внутренних узлов:
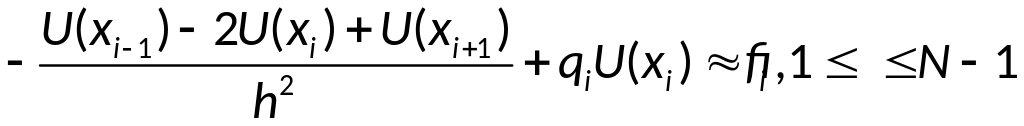
Теперь потребуем,
чтобы значения искомой сеточной функции
![]() удовлетворяли во
всех внутренних узлах сетки уравнениям
в которых знак приближенного равенство
заменен на знак равенства:
удовлетворяли во
всех внутренних узлах сетки уравнениям
в которых знак приближенного равенство
заменен на знак равенства:
 -разностная
схема.
-разностная
схема.
Приведем к виду:
![]() ,
,![]()
Видно, что система имеет вид:
![]()
Трехдиагональная матрица, где:
![]()
![]()
Прямой ход:
 ,
остальное по рекуррентным формулам:
,
остальное по рекуррентным формулам:
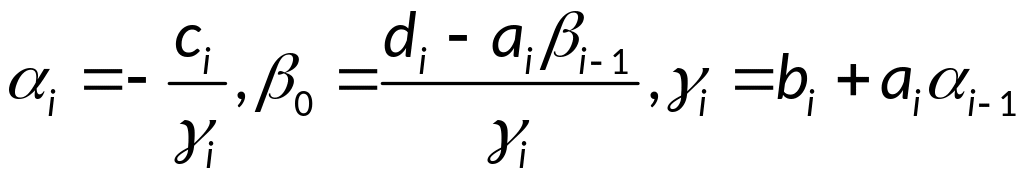 и
и

Затем обратный
ход, при
![]() :
:
![]() .
.
Оценка погрешности по правилу Рунге:
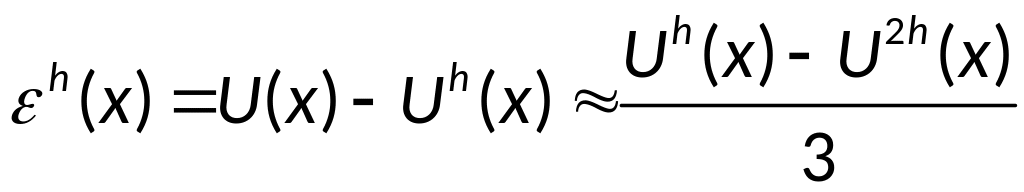 ,
применимо только в тех узлах, где известны
оба значения.
,
применимо только в тех узлах, где известны
оба значения.
30. Применение метода конечных разностей при решении двухточечной краевой задачи в случае переменного коэффициента теплопроводности.
Метод конечных разностей(или метод сеток): Область непрерывного изменения аргумента заменяют конечным множеством узлов, называемым сеткой. Вместо функций непрерывного аргумента рассматривают функции, определенные только в узлах сетки,-сеточные функции. Производные, которые входят в дифференциальное уравнение и краевые условия, заменяют их разностными аналогами. В результате краевую задачу заменяют дискретной краевой задачей(разностной схемой). Краевая задача:
![]()
В данном случае
вся сложность заключается в выборе
подходящей аппроксимации для выражения:
![]()
Введем обозначения:

Аппроксимируем:
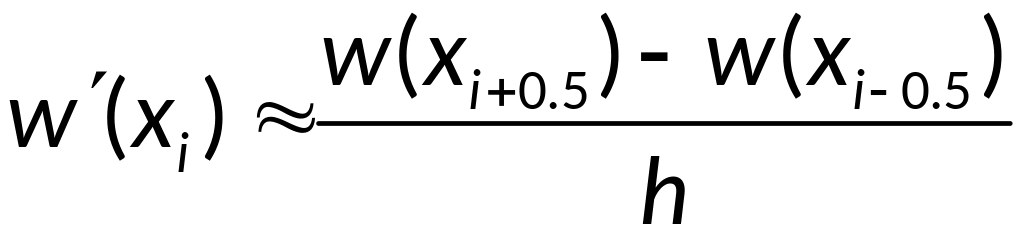
Используя далее
приближенные формулы:
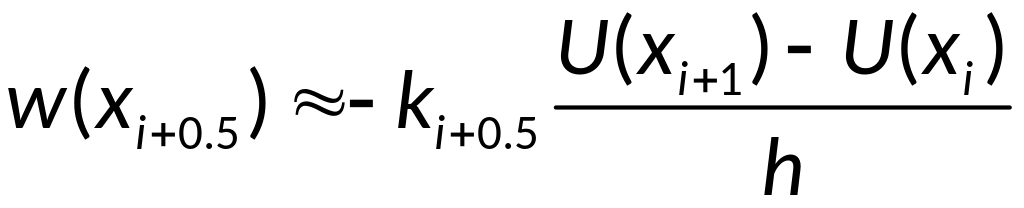
Получаем разностную
схему:
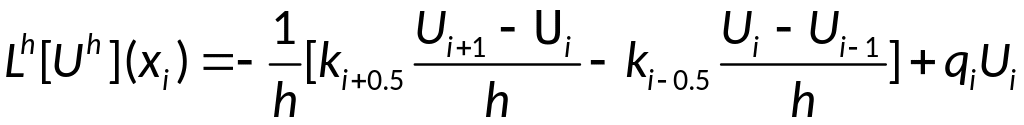
Коэффициенты:
![]()
Замечание1: При любом h существует единственное решение разностной схемы, справедлив принцип максимумов, разностная схема устойчива и сходится со вторым порядком точности, если коэффициенты k, q, f являются дважды непрерывно дифференцируемыми на отрезке [a,b] функциями.
31. Метод баланса построения разностных схем для решения двухточечной краевой задачи.
Одна из особенностей
технических задач, что изучаемая среда,
как правило, существенно неоднородна.
Этот фактор проявляется в том, что
коэффициенты дифференциальных уравнений
становятся разрывными. Предположим,
что на отрезке [a,b]
есть М точек разрыва
![]() первого рода. Будем
считать, что всюду, кроме этих точек,
коэффициенты k,
q,
f
непрерывны и
первого рода. Будем
считать, что всюду, кроме этих точек,
коэффициенты k,
q,
f
непрерывны и
![]() .
.
Допустим,
![]() -решение
задачи, если:
-решение
задачи, если:
1.
непрерывна
на отрезке [a,b]
и удовлетворяет краевым условиям
![]()
2. поток
![]() непрерывен на отрезке [a,b]
непрерывен на отрезке [a,b]
3. везде, кроме
точек разрыва,
![]() непрерывно
дифференцируема и удовлетворяет
уравнению:
непрерывно
дифференцируема и удовлетворяет
уравнению:
![]()
Применим метод баланса(или интегро-интерполяционный метод):
Запишем уравнение
теплового баланса для отрезка
![]() , где
, где
![]() ,
получаем:
,
получаем:

Воспользуемся
приближенной формулой:
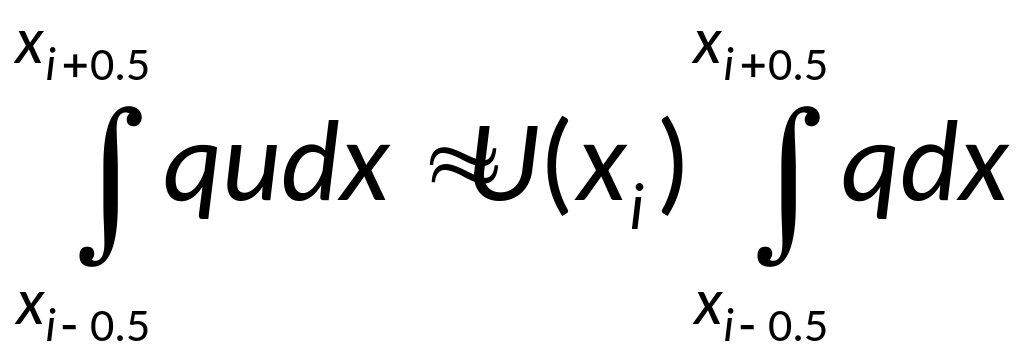 ,
поделим на
,
поделим на
![]() :
:
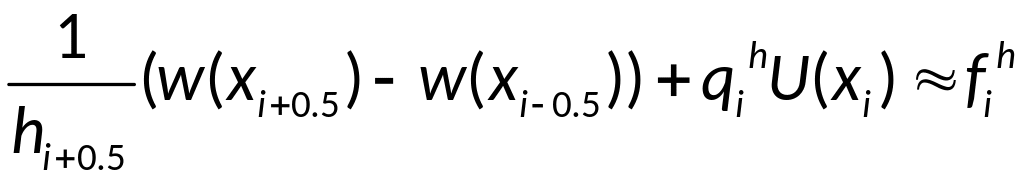 ,
где
,
где

Заметим:

Получим:
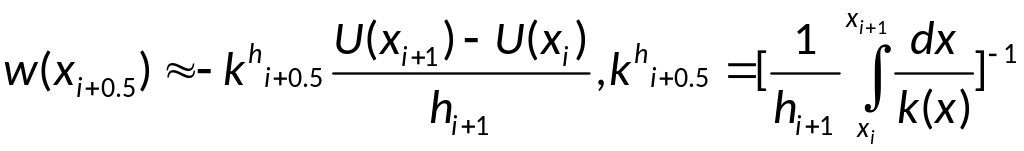 -эффективное
значение коэффициента теплопроводности
на отрезке
-эффективное
значение коэффициента теплопроводности
на отрезке
![]() .
.
Замечание1:
усредняется фактически не коэффициент
теплопроводности k(x),
а обратный к нему коэффициент
теплопроводности сопротивления
![]() .
.
В итоге:
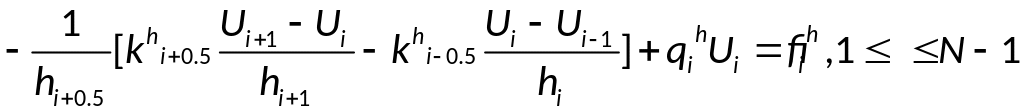 (1)
(1)
И краевые условия:
Получаем разностную схему.
Замечание2: Разностное уравнение (1) записываются единообразно во всех внутренних узлах сетки. Это означает, что рассматриваемая разностная схема относится к классу однородных разностных схем.
Х. Построение разностной схемы при решении двухточечной краевой задачи в случае граничных условий 2-го рода.
Граничные условия (ГУ) второго рода имеют вид:
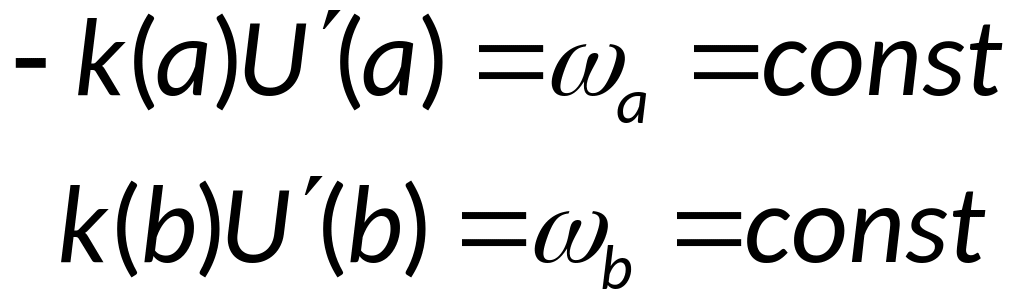
Можно аппроксимировать ГУ с 1-ым порядком точности по h:

При этом матрица A примет вид:


Аппроксимация ГУ со 2-ым порядком точности по h (используя метод баланса):
![]()
Для левой граничной точки:
![]()
![]()
![]()
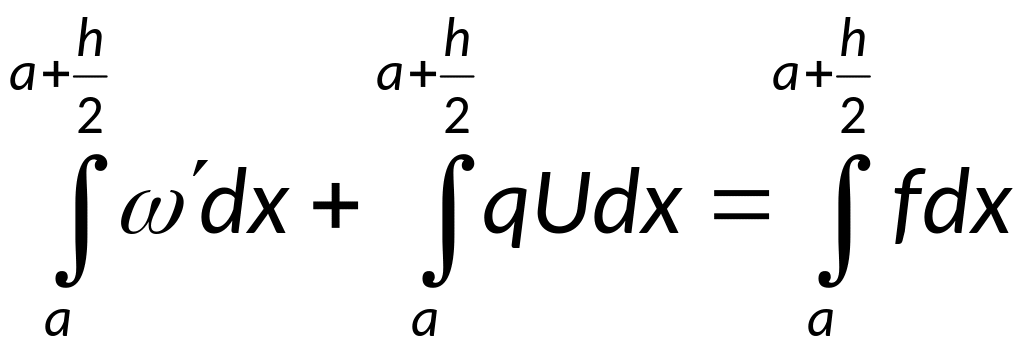
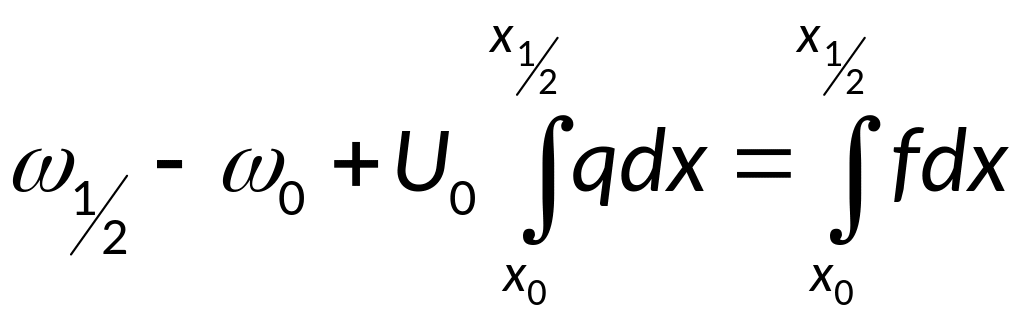
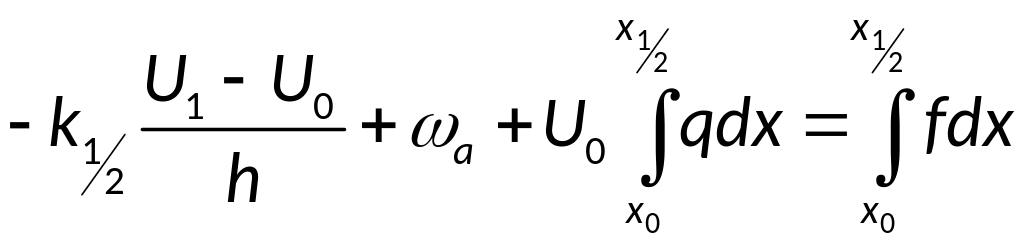
![]() - аппроксимируется
со 2-ым порядком точности по h
- аппроксимируется
со 2-ым порядком точности по h
Уравнение соответствующее левой точке:
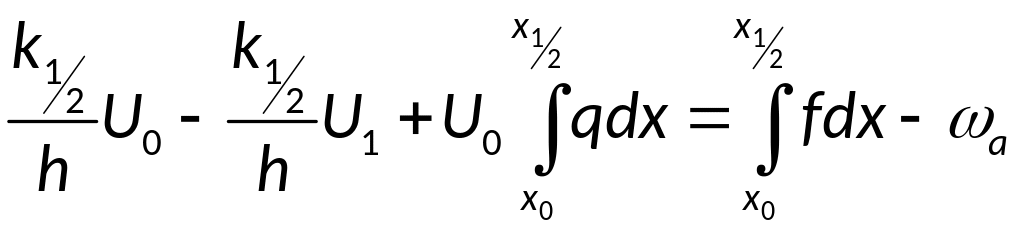
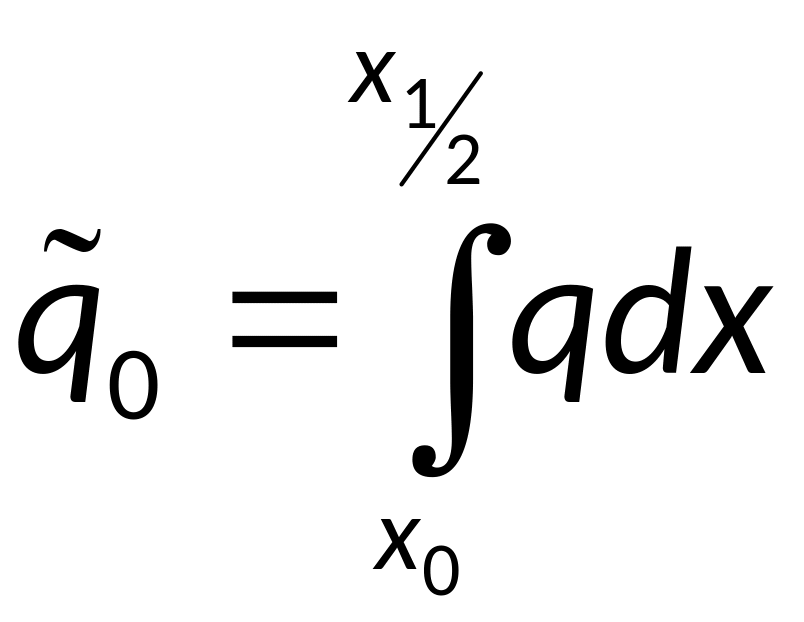 ;
;