Теорема 38. Для того чтобы n-мерный мпш был диффузионным достаточно, чтобы соответствующая ему переходная вероятность удовлетворяла условиям:

i) для некоторого , любого x равномерно по t

,

ii) существуют функции и такие, что для всех t, x

Доказательство. Проведем его для случая n=1. Действительно, в этом случае

,

,

.

Отсюда следует утверждение теоремы.

Пусть существует единственное сильное решение стохастического уравнения. Докажите, что в этом случае он является диффузионным процессом.

Теорема 18. Пусть выполнены условия 1) и 2) теоремы 34, – единственное сильное решение стохастического уравнения (22), . Тогда если - семейство переходных вероятностей процесса , то для любых и Р - п. н.

.

Теорема. Пусть выполнены условия теоремы 18, кроме того пусть коэффициенты и непрерывны по t для любых . Тогда процесс является диффузионным с коэффициентом сноса и диффузии .

Доказательство. Достаточно доказать, что для :

i) ,

ii) ,

iii) .

Заметим, что i) следует из пункта 2 теоремы 13.

( Теорема 13. 1) Пусть выполнены условия теоремы 34 и . Тогда существует положительная константа такая, что

.

2) Пусть выполнены условия теоремы 12 и , то существует константа К такая, что

. )

Установим ii). Очевидно, что в силу свойств стохастических интегралов

Заметим, что: а) из 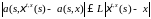следует, что

, б) . Поэтому .

Установим iii). Сначала заметим, что в силу формулы Ито

Аналогично предыдущей выкладке легко убедиться в том, что

Доказательство закончено.

Выведите обратное уравнение Колмогорова, соответствующее стохастическому уравнению (Теорема 41).

Теорема 41. Пусть - единственное сильное решение стохастического уравнения (22), коэффициенты которого непрерывны по совокупности переменных. Пусть , , причём . Тогда удовлетворяет уравнению

(41) 8.2.1. Доказательство теоремы опирается на вспомогательное утверждение.

Лемма 42. Пусть - квадратично интегрируемый мартингал, допускающий представление

, (42)

где 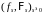– неупреждающий процесс такой, что Р - п. н. .

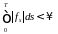Тогда Р - п. н. .

Доказательство. Без ограничения общности можно считать, что Р - п. н. . Пусть - разбиение отрезка такое, что .

Очевидно, что . Так как ,

то .

Но Р - п. н. и при Р - п. н. . Следовательно . Доказательство закончено.

Доказательство теоремы 41. Так как удовлетворяет стохастическому уравнению (36), а , то к можно применить формулу Ито, имеем

(43) Заметим, что в силу марковского свойства процесс является мартингалом относительно меры Р. Кроме того, стохастический интеграл является мартингалом относительно меры Р. Поэтому мартингалом относительно потока и меры Р является второе слагаемое правой части (43). Следовательно, в силу леммы 21 Р - п. н.

. (44)

В силу условий теоремы и непрерывности процесса по можно осуществить предельный переход равенстве (44) при . В результате уравнение (41). Осталось отметить, что 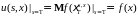. Доказательство закончено.

Выведите уравнение Фоккера-Планка-Колмогорова (Теорема 44).

Теорема 44. Пусть выполнены условия теоремы 19 (см. вопрос 30). Пусть для любого существует плотность распределения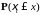 , обозначаемая через . Кроме того, пусть существуют производные , , для любых . Тогда плотность распределения удовлетворяет уравнению

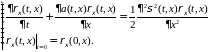(45) Замечание. Уравнение (45) обычно называют уравнением Фоккера-Планка-Колмогорова.

Доказательство теоремы 44. Пусть - бесконечно дифференцируемая функция с компактным носителем [13], а - единственное сильное решение стохастического уравнения (22). В силу формулы Ито, имеем Р - п. н.

(46)

Возьмем математическое ожидание относительно левой и правой частей (46), учитывая свойства стохастических интегралов, имеем

.

В силу условий теоремы и теоремы Фубини последнее равенство можно переписать в виде

Положим для любого х. Кроме того, в силу формулы интегрирования по частям правая часть последнего равенства будет иметь вид (в силу свойств функции )

.

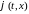Отсюда, в силу произвольности функции получаем, что удовлетворяет уравнению (42). Доказательство закончено.