
- •Очевидно, что
- •Положим . Очевидно, что из приведенных построений следует, что
- •Для любого момента времени t и
- •Тогда решение уравнения (17) имеет вид для .
- •Теорема 26. Пусть выполнены условия теоремы 25. Тогда выходной поток является пуассоновским с интенсивностью .
- •Это утверждение следует из того, что и усиленного закона больших чисел.
- •Доказательство. Пусть . Очевидно, что (докажите это неравенство самостоятельно). Заметим, что Поэтому (5)
- •Теорема 38. Для того чтобы n-мерный мпш был диффузионным достаточно, чтобы соответствующая ему переходная вероятность удовлетворяла условиям:
Мультивариантный точечный процесс, k-вариантный точечный процесс.
Определение.
Мультивариантным
точечным процессом
на
 называется последовательность
называется последовательность
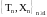 ,
где
,
где
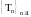 -
марковские моменты такие, что: а)
-
марковские моменты такие, что: а)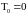 ;
б)
;
б)
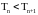 на
множестве
на
множестве
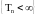 ;
в)
;
в)
 на множестве
на множестве
 ;
а
;
а
 на множестве
и
на множестве
и
 на множестве
где
на множестве
где
 -
некоторая "фиктивная" точка, причём
-
некоторая "фиктивная" точка, причём
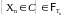 для
для
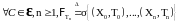 .
.
По
мультивариантному точечному процессу
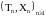 легко
построить опциональный случайный
процесс
легко
построить опциональный случайный
процесс
 с кусочно-постоянными траекториями.
Действительно, для любого n
положим
с кусочно-постоянными траекториями.
Действительно, для любого n
положим
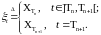
Очевидно, что таким образом построенный случайный процесс является согласованным и его траектории непрерывны справа и имеют конечный левый предел, т. е. принадлежат пространству Скорохода.
Обозначим
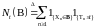 - число попаданий мультивариантного
точечного процесса в множество
- число попаданий мультивариантного
точечного процесса в множество
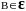 за время t.
Очевидно, что
за время t.
Очевидно, что
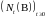 считающий
процесс, поэтому
считающий
процесс, поэтому
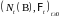 -
субмартингал (относительно меры Р).
Стало быть, по теореме Дуба-Мейера
существует единственный предсказуемый
возрастающий процесс
-
субмартингал (относительно меры Р).
Стало быть, по теореме Дуба-Мейера
существует единственный предсказуемый
возрастающий процесс
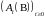 такой,
что
такой,
что
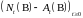 мартингал,
т. е. - компенсатор.
мартингал,
т. е. - компенсатор.
Определение.
Пусть Е
- конечное или счётное множество, причем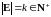 ,
в этом случае мультивариантный точечный
процесс будем называть k-вариантным.
,
в этом случае мультивариантный точечный
процесс будем называть k-вариантным.
Пусть
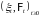 ,
где
,
где
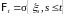 опциональный процесс построенный по
мультивариантному точечному процессу
с кусочно-постоянными со значениями в
Е,
где Е
- конечное или счетное множество. Через
опциональный процесс построенный по
мультивариантному точечному процессу
с кусочно-постоянными со значениями в
Е,
где Е
- конечное или счетное множество. Через
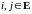 обозначим
элементы множества Е
и назовем их состояниями.
Пусть
обозначим
элементы множества Е
и назовем их состояниями.
Пусть
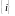 -
одноточечное множество, т.е.
-
одноточечное множество, т.е.
 .
Через
.
Через
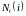 обозначим
число попаданий процесса
за
время t
в состояние i.
Очевидно, что: 1)
обозначим
число попаданий процесса
за
время t
в состояние i.
Очевидно, что: 1)
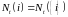 ,
2)
,
2)
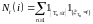 ,
где
марковские
моменты такие, что
,
где
марковские
моменты такие, что
 .
Справедливо утверждение.
.
Справедливо утверждение.
Предложение
1. Пусть
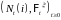 -
считающий процесс. Тогда для любых
-
считающий процесс. Тогда для любых
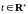 и
и
 Р
- п. н. справедливы представления:
Р
- п. н. справедливы представления:
1)если
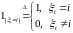 ,
то
,
то
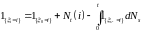 ,
,
где
 ,
,
2)
Доказательство.
1) Так как
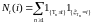 ,
то, очевидно, что P
– п. н. для любых
,
то, очевидно, что P
– п. н. для любых
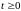 ,
,
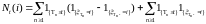 .
.
Получившееся
равенство перепишем в виде интеграла
Римана-Стилтьеса, имеем P
– п. н.
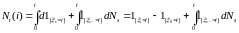 .
.
Отсюда следует первое утверждение предложения.
2)
Так как марковские моменты
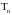 нагружают
процесс
,
то
P
– п. н. для любого
нагружают
процесс
,
то
P
– п. н. для любого
 .
Поэтому
.
Поэтому
 P
– п. н. для любого
.
Следовательно, P
– п. н. для любых
,
,
имеем
P
– п. н. для любого
.
Следовательно, P
– п. н. для любых
,
,
имеем
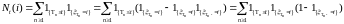 Последнее
равенство перепишем в виде интеграла
Римана – Стилтьеса, имеем P
– п. н.
Последнее
равенство перепишем в виде интеграла
Римана – Стилтьеса, имеем P
– п. н.
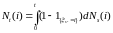 .
Доказательство закончено.
.
Доказательство закончено.
Матрица интенсивностей перехода. Условия существования матрицы интенсивностей перехода (Теорема 3).
Пусть
на стохастическом базисе
 задан опциональный процесс
со значениями в Е,
где Е
– конечное
или счетное множество. Пусть
задан опциональный процесс
со значениями в Е,
где Е
– конечное
или счетное множество. Пусть
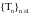 –
последовательность марковских моментов,
которая исчерпывает все скачки процесса
.
Без ограничения общности можно считать,
что
–
последовательность марковских моментов,
которая исчерпывает все скачки процесса
.
Без ограничения общности можно считать,
что
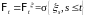 .
Пусть
.
Пусть
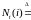
 -
считающий процесс, а
-
считающий процесс, а
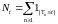 ,
относительно которых мы будем предполагать,
что выполняются условия
(N):
,
относительно которых мы будем предполагать,
что выполняются условия
(N):
i)
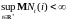 для любого
;
для любого
;
ii)
 .
.
Если
выполнено условие
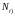 ,то
у считающего процесса
существует
,то
у считающего процесса
существует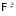 -
компенсатор
-
компенсатор
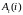 ,
относительно которого мы будем полагать,
что выполняется условие
(А):
,
относительно которого мы будем полагать,
что выполняется условие
(А):
P
– п. н. для
любых
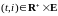
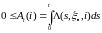 ,
причем
,
причем
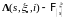 измерима, где
измерима, где
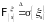 .
.
Предложение
2. Пусть
опциональный
случайный процесс с конечным или счетным
множеством состояний E,
а
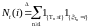 -считающий
процесс. Пусть выполняются условия (N),
(А).
Тогда существует измеримая функция
-считающий
процесс. Пусть выполняются условия (N),
(А).
Тогда существует измеримая функция
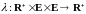 ,
обозначаемая
,
обозначаемая
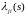 такая, что:
такая, что:
1) почти всюду относительно меры Лебега:
i)
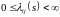 для
любых
для
любых
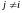 ,
,
ii)
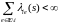 для любых
;
для любых
;
2) компенсатор
считающего процесса
имеет вид
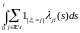 ;
;
3) компенсатор
процесса
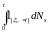 имеет вид
имеет вид
 .
.
Доказательство.
1) Рассмотрим считающий процесс
,
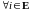 .
В силу пункта 2) предложения 1 и теоремы
Блекуэлла для любой
предсказуемой ограниченной неотрицательной
функции
.
В силу пункта 2) предложения 1 и теоремы
Блекуэлла для любой
предсказуемой ограниченной неотрицательной
функции
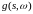 справедливо равенство:
справедливо равенство:

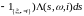 . (7)
. (7)
Из
условия (А)
следует, что
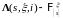 - измерима, поэтому в силу теоремы Бореля,
существует измеримая функция
,
обозначаемая через
- измерима, поэтому в силу теоремы Бореля,
существует измеримая функция
,
обозначаемая через
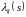 ,
такая, что
,
такая, что
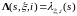 почти всюду относительно меры
почти всюду относительно меры
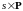 .
Очевидно, что
.
Очевидно, что
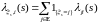 .
Поэтому (7) можно переписать в виде
.
Поэтому (7) можно переписать в виде
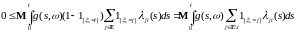 .
.
Из последнего равенства, в силу произвольности функции получаем, что:
1)
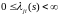 для
для
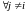 почти всех s,
2)
почти всех s,
2)
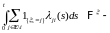 -компенсатор
считающего процесса
.
Таким образом, второе утверждение
предложения установлено.
-компенсатор
считающего процесса
.
Таким образом, второе утверждение
предложения установлено.
3)
Рассмотрим процесс
.
Из определения процесса
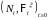 и условий предложения для любой
- предсказуемой ограниченной неотрицательной
функции
и условий предложения для любой
- предсказуемой ограниченной неотрицательной
функции
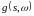 определен
и конечен интеграл
определен
и конечен интеграл
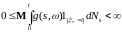 для любого
для любого
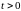 .
В силу условий предположения и свойств
интеграла Стилтьеса, имеем
.
В силу условий предположения и свойств
интеграла Стилтьеса, имеем
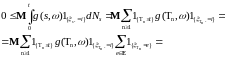
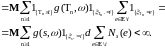 (8)
(8)
Ранее
мы выяснили, что
-
компенсатор считающего процесса
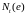 имеет вид
имеет вид
 .
Поэтому для любых t,i
из (8) имеем
.
Поэтому для любых t,i
из (8) имеем
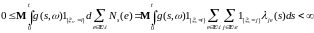
Следовательно,
в силу произвольности функции
,
получаем
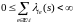 для любых
и почти всех s.
Отсюда, в силу теоремы Блекуэлла и
произвольности
,
получаем, что предсказуемый процесс
является компенсатором процесса
для любых
и почти всех s.
Отсюда, в силу теоремы Блекуэлла и
произвольности
,
получаем, что предсказуемый процесс
является компенсатором процесса
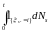 .
Доказательство закончено.
.
Доказательство закончено.
Из предложения 2 следует определение.
Определение.
Измеримую функцию
,
обозначаемую через
,
где
 ,
назовем матрицей
интенсивности перехода
опционального процесса
,
назовем матрицей
интенсивности перехода
опционального процесса
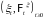 с
конечным или счетным числом состояний,
если выполняются условия:
с
конечным или счетным числом состояний,
если выполняются условия:
1) для почти всех s
i) для любых ,
ii)
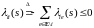 для
любого
,
для
любого
,
iii)
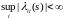 .
.
2) относительно потока и меры P процессы и :
i)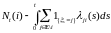 ,
,
ii)
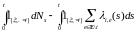
являются мартингалами.
Теорема 3. Пусть выполнены условния (N) и (A), тогда матрица интенсивности перехода существует у опционального процесса с конечным или счетным числом состояний.
Пусть
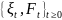 - опциональный процесс с кусочно-постоянными
траекториями, у которого существует
матрица интенсивностей перехода. Тогда
справедливо равенство
- опциональный процесс с кусочно-постоянными
траекториями, у которого существует
матрица интенсивностей перехода. Тогда
справедливо равенство

где
 – мартингал (Теорема
4).
– мартингал (Теорема
4).
Теорема
4. Пусть
выполнены условия (N),
(А)
(см. вопрос 2). И пусть
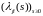 - матрица интенсивности перехода
опционального процесса
с конечным или счетным числом состояний.
Тогда Р –
п.н. справедливо представление для любых
и
.
- матрица интенсивности перехода
опционального процесса
с конечным или счетным числом состояний.
Тогда Р –
п.н. справедливо представление для любых
и
.
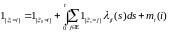 . (9)
. (9)
где
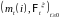 -
мартингал.
-
мартингал.
Доказательство. Первое утверждение следует из предложения 2. Второе утверждение теоремы следует из предложений 1 и 2.
Действительно, из пункта 1) предложения 1 и пункта 3 предложения 2, имеем P – п.н.
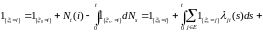
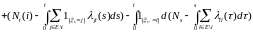
Здесь
мы учли, что
 .
Для завершения доказательства осталось
лишь заметить, что в силу пунктов 2) и 3)
предложения 2
.
Для завершения доказательства осталось
лишь заметить, что в силу пунктов 2) и 3)
предложения 2
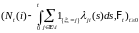 и
и
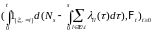 являются мартингалами относительно
меры P.
Доказательство закончено.
являются мартингалами относительно
меры P.
Доказательство закончено.
Замечание.
Предположим, что
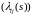 - матрица интенсивности перехода
удовлетворяет условиям:
- матрица интенсивности перехода
удовлетворяет условиям:
1)
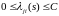 для
для
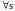 и
,
и
,
2)
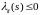 ,
,
3)
 .
.
Тогда
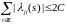 .
Действительно, из условий 1) – 3) следует,
что для
.
Действительно, из условий 1) – 3) следует,
что для
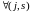
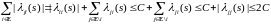 .
.
Пусть - опциональный процесс с конечным или счётным количеством состояний имеет матрицу интенсивностей перехода. Выведите систему уравнений Колмогорова для
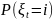 (Теорема
5).
(Теорема
5).
Теорема
5. Пусть
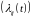 - матрица интенсивностей перехода
процесса
- матрица интенсивностей перехода
процесса
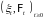 .
Тогда
.
Тогда
 удовлетворяет
системе уравнений для
удовлетворяет
системе уравнений для
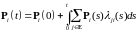 .
(10)
.
(10)
(на лекциях доказательства не было, но я его приложил из печатных)
Доказательство.
Возьмем математическое ожидание
относительно левой и правой частей (9),
учитывая, что
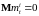 для
для
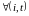 ,
имеем
,
имеем
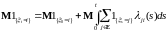 .
.
Так
как
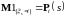 для
для
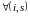 ,
то в силу теоремы Фубини из последнего
равенства имеем
,
то в силу теоремы Фубини из последнего
равенства имеем
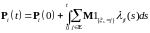 .
.
Отсюда,
в силу того, что
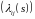 детерминированная функция, получаем
(10). Доказательство закончено.
детерминированная функция, получаем
(10). Доказательство закончено.
Замечание. Процесс , распределение вероятностей которого удовлетворяет (10) называют скачкообразным марковским процессом с конечным или счетным числом состояний. Система уравнений (10) называется прямым уравнением Колмогорова для марковских процессов с конечным или счетным числом состояний.
Установите достаточные условия существования и единственности решения уравнения Колмогорова для ??? процесса с конечным или счётным числом состояний (Теорема 6)
Теорема
6. Пусть
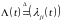 -
размера
-
размера
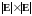 матрица интенсивности перехода такая,
что: 1)
матрица интенсивности перехода такая,
что: 1)
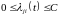 для
для
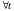 и
,
и
,
2)
 для
для
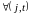 ,
3)
,
3)
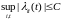 .
Тогда в классе
.
Тогда в классе
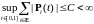 решение уравнения (10) существует и
единственно.
решение уравнения (10) существует и
единственно.
Доказательство теоремы 6 опирается на лемму.
Лемма
(Гронуолла - Беллмана). Пусть
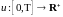 ,
,
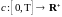 -
измеримая
функция, обозначаемые через u(t)
и c(s),
соответственно, такие, что: а)
-
измеримая
функция, обозначаемые через u(t)
и c(s),
соответственно, такие, что: а)
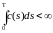 ;
б)
;
б)
 .
Тогда для
.
Тогда для
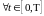 справедливо неравенство
справедливо неравенство
 .
.
Доказательство.
Очевидно неравенство для
 .
.
Последнее
можно переписать в виде
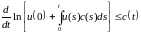 .
Отсюда следует, что
.
Отсюда следует, что
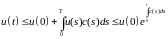 .
Доказательство закончено.
.
Доказательство закончено.
Доказательство теоремы 6. Сначала заметим, что (10) можно переписать в виде
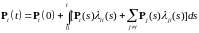 .
.
Отсюда, в силу формулы Коши (для обыкновенного линейного неоднородного уравнения первого порядка), имеем
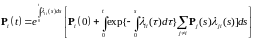 . (11)
. (11)
Заметим,
что
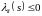 ,
поэтому имеем неравенства:
,
поэтому имеем неравенства:
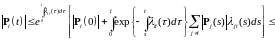
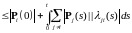 .
.
Отсюда в силу теоремы Фубини следует, что

 .
.
(Здесь
мы учли, что
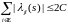 для
для
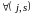 ).
).
Таким образом, мы пришли к неравенству
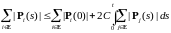 .
.
В
силу леммы Гронуолла - Беллмана, имеем
 .
.
Отсюда следует существование решения системы уравнений (10).
Установим
теперь единственность решения системы
(10). Пусть
 ,
l
= 1,2, - два решения системы (10). Поэтому в
силу (11) для
справедливо
представление
,
l
= 1,2, - два решения системы (10). Поэтому в
силу (11) для
справедливо
представление
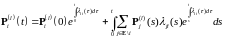 . (12)
. (12)
Обозначим
 .
Из (12) следуют неравенства
.
Из (12) следуют неравенства
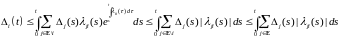 .
.
Отсюда, в силу теоремы Фубини, имеем для любого t
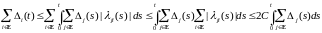 .
.
Поэтому,
в силу леммы Гронуолла - Беллмана, имеем
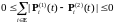 .
Отсюда следует утверждение теоремы.
.
Отсюда следует утверждение теоремы.
Вероятностная интерпретация интенсивности (Теорема 8).
Пусть
имеется m-вариантный
точечный процесс
,
а
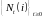 ,
,
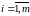 ,
- считающий процесс,
,
- считающий процесс,
 .
Пусть
.
Пусть
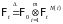 ,
где
,
где
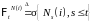 .
Предположим, что
.
Предположим, что
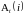 - компенсатор точечного процесса
,
причем
- компенсатор точечного процесса
,
причем
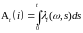 ,
где
,
где
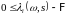 -
измеримая интенсивность.
-
измеримая интенсивность.
Теорема
8. Для
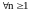 на множестве
Р
- п. н.
на множестве
Р
- п. н.
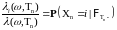 ,
,
где
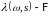 -
интенсивность считающего процесса
-
интенсивность считающего процесса
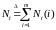 ,
т. е.
,
т. е.
 .
.
Доказательство.
Пусть
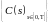 –
ограниченный,
–
ограниченный,
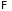 -
предсказуемый, случайный процесс, причем
-
предсказуемый, случайный процесс, причем
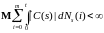 .
Очевидно, что
.
Очевидно, что
 .
(14)
.
(14)
Без
ограничения общности, можно считать,
что
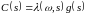 ,
где
,
где
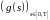 -
ограниченный предсказуемый процесс.
Из (14) имеем
-
ограниченный предсказуемый процесс.
Из (14) имеем
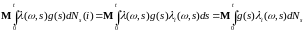 .
(15)
.
(15)
Пусть
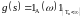 ,
где
,
где
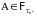 .
Тогда (15) можно переписать в виде
.
Тогда (15) можно переписать в виде
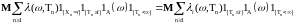 .
.
Отсюда, в силу произвольности t, следует равенство
 .
.
Следовательно
 .
.
В силу правильности множества получаем, что
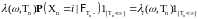 .
.
Доказательство закончено.
Определение случайной меры, меры Далиан, компенсатор опциональной случайной меры (Теорема 11).
Напомним
определение
 - конечной меры.
- конечной меры.
Определение.
Мера
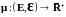 называется
- конечной,
если для любого замкнутого ограниченного
множества
называется
- конечной,
если для любого замкнутого ограниченного
множества
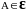 существует
последовательность множеств
существует
последовательность множеств
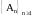 ,
где
,
где
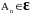 ,
такая, что: a)
,
такая, что: a)
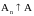 при
при
 ,
б)
,
б)
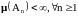 .
.
Определение.
Мера
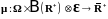 называется
случайной
и обозначается
называется
случайной
и обозначается
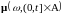 ,
где
,
где
 ,
если:
,
если:
а)
при фиксированных
и A
как функция t
является случайным процессом, б) при
фиксированных
и t
- конечная мера, в)
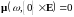 для
для
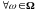 .
.
Пусть
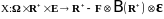 -
измеримая функция такая, что определён
интеграл Лебега
-
измеримая функция такая, что определён
интеграл Лебега
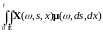 обозначаемый
обозначаемый
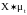 .
.
Обозначим
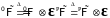 .
.
Определение.
Случайная мера
называется опциональной
(предсказуемой),
если для любой неотрицательной
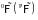 - измеримой функции Х процесс
- измеримой функции Х процесс
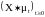 является опциональным (предсказуемым).
является опциональным (предсказуемым).
Обозначим
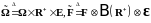 .
.
Определение.
Меру
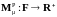 назовем
мерой Долиан,
если
назовем
мерой Долиан,
если
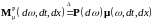 .
.
Отсюда
следует, что для всякой неотрицательной
 -
измеримой
функции X(,
t,
x)
определен интеграл по мере Долиан:
-
измеримой
функции X(,
t,
x)
определен интеграл по мере Долиан:
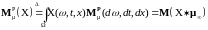 .
.
Определение.
Мера Долиан
 называется конечной,
если
называется конечной,
если
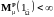 .
Определение.
Будем говорить, что опциональная
случайная мера
принадлежит классу
.
Определение.
Будем говорить, что опциональная
случайная мера
принадлежит классу
 (пишем
(пишем
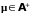 ),
если
.
),
если
.
Определение.
Mepa Долиан
называется
- -конечной,
если существует последовательность
множеств
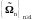 таких,
что
таких,
что
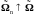 ,
где
,
где
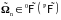 ,
и
,
и
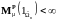 для
.
для
.
Определение.
Будем говорить, что опциональная
случайная мера
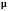 принадлежит классу
принадлежит классу
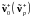 (пишем
(пишем
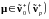 )
если
,
где
и
.
)
если
,
где
и
.
Теорема
9.
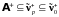 .
.
Определение.
Будем говорить, что случайные меры
и
 совпадают
Р
- п. н. (пишем
совпадают
Р
- п. н. (пишем
 ),
если для любой неотрицательной
),
если для любой неотрицательной
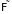 -
измеримой
функции Х
-
измеримой
функции Х
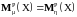 .
.
Из этого определения следует утверждение.
Теорема 10. Пусть и - опциональные случайные меры такие, что:
а)
для любой
-
измеримой
X;
б) хотя бы одна из них принадлежит
 .
Тогда
.
.
Тогда
.
Определение.
Компенсатором
опциональной случайной меры
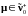 называется предсказуемая мера
называется предсказуемая мера
 (т.
е.
(т.
е.
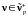 )
такая, что для любой неотрицательной,
)
такая, что для любой неотрицательной,
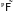 -
измеримой функции Х(
-
измеримой функции Х(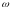 ,
t,
х)
,
t,
х)
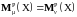 .
.
Теорема 11. У всякой опциональной случайной меры существует и притом единственный компенсатор , т. е. (с точностью до нулевой меры Р). (Доказательство следует из теоремы Дуба - Мейера).
Случайные меры и мультивариантные точечные процессы (Теорема 14).
Пусть
 -
m
- вариантный
точечный процесс, a
-
m
- вариантный
точечный процесс, a
 ,
,
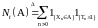 -
считающие процессы, где
-
считающие процессы, где
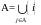 .
.
Пример.
Пусть
-
случайный процесс определённый
соотношением

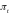 - пуассоновский случайный процесс с
интенсивностью
- пуассоновский случайный процесс с
интенсивностью
 .
Ясно, что процесс
.
Ясно, что процесс
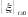 принимает
два значения {-1, 1}, причём время пребывания
в состоянии -1 или в состоянии 1 распределены
экспонен-циально с параметром
принимает
два значения {-1, 1}, причём время пребывания
в состоянии -1 или в состоянии 1 распределены
экспонен-циально с параметром
 .
Этот процесс имеет кусочно-постояные
траектории и непрерывен справа, поэтому
он опционален. Через
.
Этот процесс имеет кусочно-постояные
траектории и непрерывен справа, поэтому
он опционален. Через
 обозначим число попаданий в состояние
1(-1) за время t
процессом
.
Очевидно, что если
обозначим число попаданий в состояние
1(-1) за время t
процессом
.
Очевидно, что если

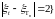 для
для

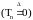 ,
то
можно построить следующим образом:
,
то
можно построить следующим образом:
 ,
,
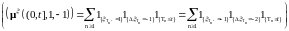 .
.
Ясно
также, что с помощью
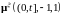 и
и
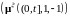 можно
описать процесс
можно
описать процесс
 ,
,
так
как
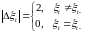 .
Легко показать, что для
.
Легко показать, что для
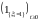
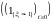 справедливо представление
справедливо представление
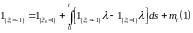
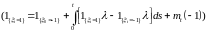 ,
,
причем
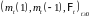 - ограниченные мартингалы (относительно
меры Р)
- ограниченные мартингалы (относительно
меры Р)
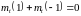 для
для
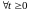 .
.
Приведённый выше пример служит основой для дальнейших построений.
Перейдем теперь к построению целочисленной случайной меры k - вариантного точечного процесса и её компенсатора.
В
предыдущих параграфах мы установили
связь между скачко-образными и
мультивариантными точечными процессами.
Итак, пусть
- скачкообразный опциональный
случайный процесс со значениями в Е,
причём
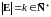 .
В соответствии с результатами параграфа
13 для процесса
определена
целочисленная случайная мера
.
В соответствии с результатами параграфа
13 для процесса
определена
целочисленная случайная мера
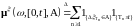 ,
где
,
где
 -
последовательность марковских моментов,
исчерпывающая скачки процесса
,
-
последовательность марковских моментов,
исчерпывающая скачки процесса
,
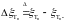 .
Очевидно, что при фиксированных
.
Очевидно, что при фиксированных
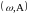
 это опциональный неубывающий процесс,
т. е.
это опциональный неубывающий процесс,
т. е.
 при t
s.
Стало быть,
при t
s.
Стало быть,
 является субмартингалом и по теореме
Дуба-Мейера существует компенсатор
является субмартингалом и по теореме
Дуба-Мейера существует компенсатор
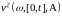 ,
т. е.
,
т. е.
 является мартингалом относительно
потока
является мартингалом относительно
потока
 и
меры Р.
Предположим
дополнительно, что
имеет неслучайную матрицу интенсивности
перехода
и
меры Р.
Предположим
дополнительно, что
имеет неслучайную матрицу интенсивности
перехода
 .
Тогда в силу теоремы 35
.
Тогда в силу теоремы 35
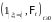 допускает
представление:
допускает
представление:
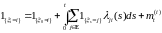 . (9)
. (9)
Обозначим
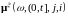 -
число переходов процесс
из
состояния j
в состояние i
за время t.
Ясно, что его можно представить в виде:
-
число переходов процесс
из
состояния j
в состояние i
за время t.
Ясно, что его можно представить в виде:
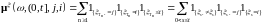 .
.
Найдём
компенсатор
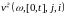 - случайной
меры
.
Сначала заметим, что
- случайной
меры
.
Сначала заметим, что
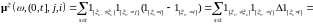
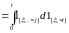 .
.
Отсюда, в силу (9), имеем:
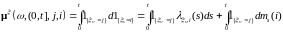 . (16)
. (16)
Заметим: 1) для Р - п. н.
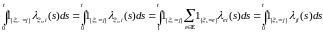 ;
;
2)
так как
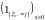 - ограниченный предсказуемый процесс,
то
- ограниченный предсказуемый процесс,
то
стохастический
интеграл
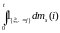 является мартингалом. Поэтому процесс
является мартингалом. Поэтому процесс
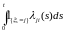 является компенсатором
-
целочисленной случайной меры относительно
меры P.
является компенсатором
-
целочисленной случайной меры относительно
меры P.
Очевидно, что
t
= t
- t-
=
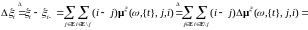
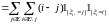 .
Учитывая, что траектория процесса
кусочно-постоянна, получаем,
.
Учитывая, что траектория процесса
кусочно-постоянна, получаем,
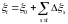 .
Поэтому
.
Поэтому
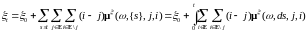 .
.
Таким образом, доказано утверждение.
Теорема
14. Пусть
 опциональный
процесс с кусочно-постоянными траекториями,
конечным или счетным множеством состояний
Е
и матрицей интенсивности переходов
опциональный
процесс с кусочно-постоянными траекториями,
конечным или счетным множеством состояний
Е
и матрицей интенсивности переходов
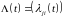 размера -
.
Тогда справедливы следующие утверждения:
размера -
.
Тогда справедливы следующие утверждения:
1)
целочисленная случайная мера
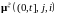 допускает представление
допускает представление
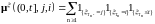 ,
,
где - последовательность марковских моментов (опциональных), исчерпывающая скачки процесса ;
2)
компенсатор
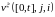 целочисленной случайной меры
имеет вид
целочисленной случайной меры
имеет вид
 ;
;
3) процесс допускает представление
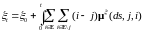 .
.
Замечание.
В общем случае, если
-
опциональный скачкообразный процесс
с кусочно-постоянными траекториями, со
значениями в
 ,
как легко показать, допускает представление
,
как легко показать, допускает представление
t
= 0
+
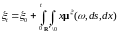 ,
,
где
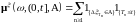 .
.
Процесс восстановления, функция восстановления (определения). Выведите уравнение восстановления (Теорема 15).
Рассмотрим
вероятностное пространство
 .
Пусть на нём задана последовательность
неотрицательных, независимых в
совокупности, одинаково распределённых,
случайных величин
.
Пусть на нём задана последовательность
неотрицательных, независимых в
совокупности, одинаково распределённых,
случайных величин
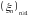 ,
с функцией распределения
,
с функцией распределения
 .
Обозначим
.
Обозначим
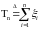 и
и
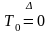 .
Положим
.
Положим
 - считающий процесс. Этот процесс в
теории восстановления называют простым
процессом восстановления,
который имеет следующую интерпретацию:
в момент времени нуль начинает
функционировать некоторое устройство,
которое функционирует до момента времени
- считающий процесс. Этот процесс в
теории восстановления называют простым
процессом восстановления,
который имеет следующую интерпретацию:
в момент времени нуль начинает
функционировать некоторое устройство,
которое функционирует до момента времени
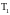 ,
в момент времени
оно выходит из строя, т.е. ломается, его
мгновенно ремонтируют и снова это
устройство нормально функционирует до
момента времени
,
в момент времени
оно выходит из строя, т.е. ломается, его
мгновенно ремонтируют и снова это
устройство нормально функционирует до
момента времени
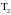 ,
в момент времени
оно выходит из строя и его мгновенно
ремонтируют и т. д. Очевидно, что N(t)
- это число восстановлений устройства
к моменту времени t.
,
в момент времени
оно выходит из строя и его мгновенно
ремонтируют и т. д. Очевидно, что N(t)
- это число восстановлений устройства
к моменту времени t.
Обозначим
через
 - функцию распределения случайной
величины
- функцию распределения случайной
величины
,
т.е.
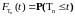 .
Так как
,
то
.
Так как
,
то
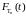 равно n-кратной
свёртке функции распределения
,
которую обозначим через
равно n-кратной
свёртке функции распределения
,
которую обозначим через
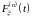 .
Ясно, что
.
Ясно, что
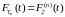 .
.
Обозначим
через
 –
среднее число восстановлений за время
t,
называемое функцией
восстановления.
Ясно, что
–
среднее число восстановлений за время
t,
называемое функцией
восстановления.
Ясно, что
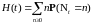 .
.
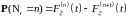 .
.
Доказательство.
Очевидно, что
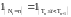 .
Рассмотрим
.
Рассмотрим
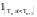 ,
очевидно
,
очевидно

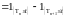 .
.
Последнее
равенство имеет место, так как
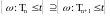 .
Возьмём теперь математическое ожидание
относительно левой и правой частей
получившегося равенства. В результате
получаем утверждени.
.
Возьмём теперь математическое ожидание
относительно левой и правой частей
получившегося равенства. В результате
получаем утверждени.
Доказательство закончено.
Теорема 15. H(t) удовлетворяет уравнению
 (1)
(1)
(Уравнение (1) называют уравнением восстановления).
Доказательство. Из определения функции восстановления H(t) и теоремы 1, имеем
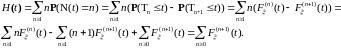
Так
как
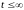 ,
то
,
то
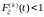 .
Поэтому ряд
.
Поэтому ряд
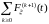 - сходится. Отсюда следует:
- сходится. Отсюда следует:
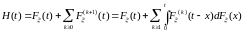 .
.
Поэтому в силу теоремы Фубини имеем:
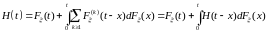 .
.
Доказательство закончено.
Узловая теорема теории восстановления (Теорема 17).
Теорема
17 (Узловая).
Пусть
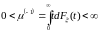 .
Пусть P
– п.н.
.
Пусть P
– п.н.
 при
.
Тогда
при
.
Тогда
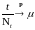 при
при
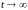 .
.
Доказательство
(набросок). Так как
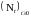 –
точечный процесс, то
–
точечный процесс, то
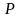 - п. н.
- п. н.
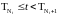 .
Разделим правую и левую части этого
неравенства на
.
Разделим правую и левую части этого
неравенства на
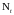 ,
имеем
,
имеем
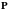 -
п. н.
-
п. н.
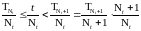 .
.
Очевидно
-
п. н.
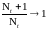 при
.
Поэтому
при
.
Поэтому
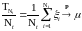 при
в силу закона больших чисел. Доказательство
закончено.
при
в силу закона больших чисел. Доказательство
закончено.
Выведите уравнение, описывающее эволюцию длины очереди (Теорема 18).
Пусть
на стохастическом базисе
заданы 2 точечных процесса
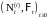 , i=1,2,
и неотрицательная, интегрируемая,
, i=1,2,
и неотрицательная, интегрируемая,
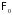 -
измеримая случайная величина
-
измеримая случайная величина
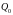 .
.
Определение.
Точечный процесс
 будем называть входным
потоком.
будем называть входным
потоком.
Определение.
Случайную величину
 - измеримую
будем называть внутренним
состоянием
или начальной
очередью.
- измеримую
будем называть внутренним
состоянием
или начальной
очередью.
Определение.
Пусть
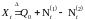 ,
а
,
а
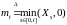 .
Процесс
.
Процесс
 назовём
простым
процессом обслуживания
или очередью.
назовём
простым
процессом обслуживания
или очередью.
Теорема
18. Пусть
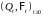 – простой процесс обслуживания. Тогда
он допускает представление P
–п. н.
– простой процесс обслуживания. Тогда
он допускает представление P
–п. н.
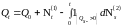 . (4)
. (4)
Доказательство.
Момент времени
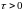 является моментом скачка вниз процесса
является моментом скачка вниз процесса
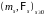 если и только если выполняются условия:
а)
если и только если выполняются условия:
а)
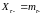 ,
,
б)
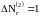 .
Поэтому
-
п. н.
.
Поэтому
-
п. н.
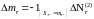 . (5)
. (5)
Так
как
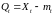 ,
то из (5) следует, что P
- п. н.
,
то из (5) следует, что P
- п. н.
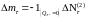 . (6)
. (6)
Из (6) следует, что P - п. н.
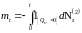 . (7)
. (7)
Очевидно,
что
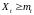 P
- п. н. для любого
,
поэтому
P
- п. н. для любого
,
поэтому
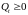 P
- п. н. для любого
.
Из определения процесса
следует, что для любого
P
- п. н., в силу (7),
P
- п. н. для любого
.
Из определения процесса
следует, что для любого
P
- п. н., в силу (7),
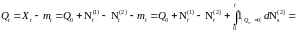
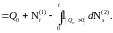
Отсюда следует утверждение теоремы.
Определение.
Точечный процесс
 ,
определяемый равенством
,
определяемый равенством
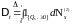 ,
называется выходным
потоком.
,
называется выходным
потоком.
При каких условиях решения стохастического уравнения, описывающего эволюцию длины очереди, имеет единственное сильное решение (Теорема 19).
Без
ограничения общности можно считать,
что
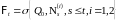 .
.
Определение. Будем говорить, что
(4)
(4)
имеет сильное
решение,
если для любого
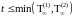
 - измеримо, Р
- п. н.
- измеримо, Р
- п. н.
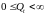 и
обращает (4) в тождество.
и
обращает (4) в тождество.
Определение.
Пусть
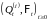 – два решения уравнения (4), причём
– два решения уравнения (4), причём
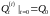 .
Будем говорить, что (4) имеет единственное
сильное решение,
если
.
Будем говорить, что (4) имеет единственное
сильное решение,
если
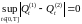 Р
- п. н., где
Р
- п. н., где
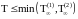 .
.
Теорема 19.Уравнение (4) имеет единственное решение.
Доказательство. Из уравнения (4) следует, что для любого Р - п. н.
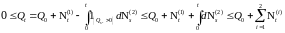 .
.
Отсюда
следует, что
 Р
- п. н. для любого
Р
- п. н. для любого
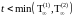 .
.
Заметим, что если решение уравнения (4) существует, то оно имеет кусочно-постоянную траекторию. Поэтому доказательство того факта,
что
- измеримо проведём по индукции. Пусть
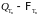 - измеримо. Покажем, что
- измеримо. Покажем, что
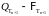 -
измеримо, где
и
-
измеримо, где
и
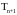 –
марковские моменты, которые нагружают
простой процесс обслуживания. Из (4)
следует, что при
–
марковские моменты, которые нагружают
простой процесс обслуживания. Из (4)
следует, что при
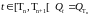 Р
- п. н. Поэтому при
Р
- п. н. Поэтому при
 Р
- п. н.
Р
- п. н.
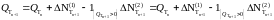 .
.
Из последнего равенства следует, что - измеримо. Таким образом, основной шаг индукции обоснован, а вместе с ним установлено существование решения уравнения (4).
Перейдём
теперь к доказательству единственности
решения (4). Его мы также проведём по
индукции. Пусть
–
два решения уравнения (4), причём
.
Так как
 имеет
кусочно-постоянные траектории, то Р
- п. н. для
имеет
кусочно-постоянные траектории, то Р
- п. н. для
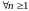
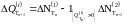 .
(8)
.
(8)
Рассмотрим
разность
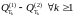 .
Пусть
.
Пусть
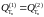 Р
- п. н. Покажем, что
Р
- п. н. Покажем, что
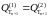 Р
- п. н. Из (8) следует, что Р
- п. н.
Р
- п. н. Из (8) следует, что Р
- п. н.
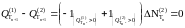 .
.
Отсюда следует, что основной шаг индукции доказан, а вместе с ним и утверждение теоремы.
Выведите уравнение, описывающее эволюцию распределения вероятностей длины очереди (Теорема 20).
Теорема
20. Пусть для
любого
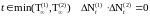 Р
- п. н. Пусть
Р
- п. н. Пусть
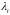 и
и
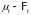 измеримы
интенсивности точечных процессов
измеримы
интенсивности точечных процессов
 и
и
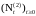 ,
а
,
а
 ,
,
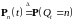 .
Тогда для любого
.
Тогда для любого
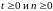
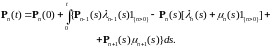 (9)
(9)
Доказательство.
Рассмотрим
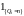 .
В силу условий теоремы, имеем
.
В силу условий теоремы, имеем
 (10)
(10)
Заметим теперь, что:
i)
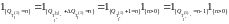 . (11)
. (11)
ii)
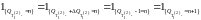 (12)
(12)
Поэтому (10) с учетом (11) и (12) можно переписать в виде:
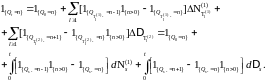 (13)
(13)
Возьмем математическое ожидание относительно левой и правой частей равенства (13). Учитывая, что:
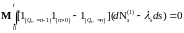 ,
,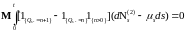 ,
,
Имеем
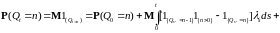
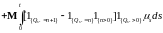 .
.
В силу теоремы Фубини и того, что мера Лебега одноточечных множеств равна нулю, последнее равенство можно переписать в виде:
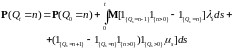 (14)
(14)
Заметим
теперь, что для любого
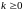 имеем:
имеем:
i)
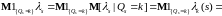 (15)
(15)
 ,
,
ii)
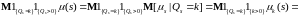
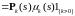 . (16)
. (16)
Поэтому (14) с учетом (15), (16) будет иметь вид (9). Доказательство закончено.
Следствие.
Пусть выполнены условия теоремы 20. Тогда
для любых
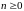 и
почти всех t
существует производная
и
почти всех t
существует производная
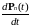 и
и
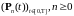 ,
удовлетворяет уравнению Колмогорова:
,
удовлетворяет уравнению Колмогорова:
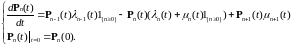 (17)
(17)
Доказательство.
Из доказательства теоремы 9 следует,
что для любого
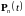 абсолютно непрерывнa
относительно меры Лебега. Отсюда, в силу
теоремы Радона – Никодима, существует
плотность
для почти всех t.
Отсюда следует утверждение следствия.
абсолютно непрерывнa
относительно меры Лебега. Отсюда, в силу
теоремы Радона – Никодима, существует
плотность
для почти всех t.
Отсюда следует утверждение следствия.
Опишите простейшую систему массового обслуживания с обратной связью (Теоремы 21-23).
Пусть
на стохастическом базисе
заданы два точечных процесса
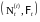 ,
с
-
измеримыми интенсивностями
,
с
-
измеримыми интенсивностями
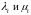 ,
соответственно, кроме того, на нем задана
последовательность бернулли-евских
случайных величин
,
соответственно, кроме того, на нем задана
последовательность бернулли-евских
случайных величин
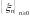 ,
принимающая значения {0,1}, причем
,
принимающая значения {0,1}, причем
 .
Предположим, что
.
Предположим, что
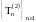 - последовательность марковских моментов,
которые нагружают точечный процесс
- последовательность марковских моментов,
которые нагружают точечный процесс
 .
Обозначим
.
Обозначим
 опциональный случайный процесс с
кусочно-постоянными траекториями:
опциональный случайный процесс с
кусочно-постоянными траекториями:
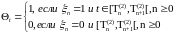
Осуществим
прореживание точечного процесса
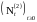 с помощью
последовательности
с помощью
последовательности
 :
:
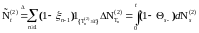
Как
и в §1, введем процессы

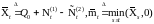 .
.
Очевидно,
что
 Р
– п. н. для любого
.
Теперь определим простой процесс
обслуживания
Р
– п. н. для любого
.
Теперь определим простой процесс
обслуживания
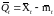 и
назовем его процессом
обслуживания для системы с обратной
связью. Ясно,
что:
и
назовем его процессом
обслуживания для системы с обратной
связью. Ясно,
что:
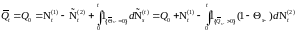
Обозначим
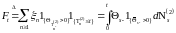
и назовем его процессом (потоком) обратной связи.
Через
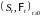 обозначим процесс:
обозначим процесс:
 (20)
(20)
