Теорема 26. Пусть выполнены условия теоремы 25. Тогда выходной поток является пуассоновским с интенсивностью .
Доказательство.
Достаточно показать, что
.
Действительно, так как
.
Отсюда, в силу свойства стохастических интегралов по мартингалу, имеющему ограниченную вариацию, и теоремы Фубини, имеем
.
В
силу условий теоремы для
,
поэтому
.
Стало быть,
.
Доказательство
закончено.
Определение винеровского процесса. Теорема существования винеровского процесса (Теорема 27).
Определение.
Случайный процесс
,
определенный на стохастическом базисе
со значениями в R1
называется винеровским
процессом,
если он обладает следующими свойствами:
i)
P-
п. н.
ii)
для любого разбиения
отрезка
,
приращения независимы в совокупности,
iii)
случайные величины
имеют нормальное распределение с
параметрами: нулевое математическое
ожидание и дисперсией
,
т.е.
,
iv)
траектории процесса
- непрерывны.
Теорема 27. Винеровский процесс существует.
Доказательство теоремы опирается на два вспомогательных утверждения
Лемма
28. Пусть
последовательность гауссовских случайных
величин такая, что существует
.Тогда X-гауссовская
случайная величина.
Доказательство.
Обозначим
.
Тогда, в силу свойства гауссовости
последовательности
,
имеем
Пусть любые
,а
,
тогда имеем
Отсюда
следует, что
Поэтому
Значит,
,
так как
и
,
при
т.е.
.
Доказательство закончено.
Доказательство
(теоремы 27)
Пусть
-
пространство измеримых квадратично
интегрируемых относительно меры Лебега
функций, заданных на отрезке [0,1] со
значениями в
.
Пусть
- ортонормированное семейство функций
в
,
т.е.
,
где
- символ
Кронекера. Обозначим
.
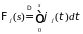Пусть
–
счетное семейство независимых в
совокупности стандартных нормальных
случайных величин. Для доказательства
теоремы достаточно доказать, что ряд
P-
п. н. cходится
для любого t
и обладает свойствами i)-iv).
Пусть
. Очевидно, что:
1)
;
2)
,
где
- скалярное
произведение в
;
3)
;
4)
,
где
- норма в
.
Обозначим
.
Очевидно, что:
1)
для любого
-
гауссовская случайная величина, причем
для любых n;
(1)
Отсюда
следует, что
- квадратично интегрируем. Рассмотрим
,
причем без ограничения общности можно
считать, что
.
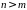В силу (1), имеем
Стало
быть, справедлив критерий Коши. Поэтому
в среднеквадратичном смысле сходится
к некоторой
,
т.е.
для любого
,
причем в силу леммы 2 случайная величина
имеет гауссовское распределение.
Построенный процесс обладает свойствами.
;
Траектории
-
непрерывны.
Действительноимеем
,
отсюда
(следует из
леммы 28).
Осталось
установить, что
–
процесс с независимыми приращениями.
Для этого достаточно показать, что
Действительно,
Доказательство закончено.
Замечания.
1) Рассмотрим
.
Отсюда следует, что
для любого
и ограниченного n
дифференцируем по t,
т.е. P-
п. н. существует
,
причем
.
Очевидно, что
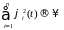при
для любого
.
2)
Из неравенства Коши-Буняковского
следует, что
.
Свойства винеровского процесса.
1)
Пусть
- винеровский процесс, не зависящий от
.
(Докажите самостоятельно).
2)
Свойство автомодальности:
для любого
процесс
,
является винеровским процессом.
Достаточно показать, что
.
Действительно
.
3)
для любого
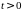– винеровский процесс.
Достаточно
показать, что
.
Действительно,
.
4) P
– п. н.
.