Это утверждение следует из того, что и усиленного закона больших чисел.

5) Процесс является винеровским процессом,

6) Это равенство следует из леммы  3.

Неравенство Дуба. Для любого

(4)

Доказательство. Пусть . Очевидно, что (докажите это неравенство самостоятельно). Заметим, что Поэтому (5)

Из равенства P – п. н. и неравенства Иенсена

получаем, что

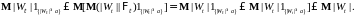Из (5) и приведенных неравенств следует неравенство Дуба.

8) Гёльдеровское свойство Леви

.

Доказательство этого утверждения проведем в два этапа: 1) сначала покажем, что P- п. н. , 2) установим неравенство

P– п. н.

1) Доказательство неравенства P – п. н. . Пусть и . Пусть имеется диадическое разбиение отрезка [0,t] точками . Тогда имеем

Обозначим . Значит, справедливо неравенство

Так как Поэтому, в силу леммы Бореля-Кантелли, имеем при

2) Установим неравенство P – п. н. . Положим . Тогда имеем

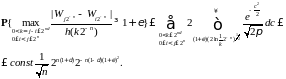
Так как , то правая часть последнего неравенства является общим членом сходящегося ряда. Следовательно, в силу леммы Бореля-Кантелли получаем утверждение.

Замечание. Из гёльдеровского свойства Леви следует, что P- п. н.

траектории винеровского процесса удовлетворяют условию Гёльдера

,

где С – некоторая константа, а

20. Докажите, что сумма квадратов приращений винеровского процесса равна приращению времени (Теорема 29).

Теорема 29. Пусть и. Пусть разбиение отрезка [s,t] такое, что , когда .

Тогда .

Доказательство. Сначала заметим, что в силу теоремы 27.

.

Поэтому для доказательства теоремы достаточно показать, что

.

Действительно, в силу теоремы Фубини, имеем:

. (2)

Заметим,

(3)

Значит, (2) с учетом (3) будет иметь вид:

Доказательство закончено.

Определение стохастического интеграла Ито для простой функции и его свойства.

Пусть на некотором стохастическом базисе задан - одномерный винеровский процесс. Целью данного параграфа является построение стохастических интегралов вида для некоторого класса функций . Сначала заметим, что интегралы такого типа нельзя определить как интегралы Римана-Стилтьеса или Лебега-Стилтьеса, так как реализация винеровского процесса имеет неограниченную вариацию на сколь угодно малых промежутках времени (последнее следует из гельдеровского свойства Леви винеровского процесса).

Определение. Измеримая (по паре переменных ) функция называется неупреждающей (по отношению к фильтрации ), если при каждом t она -измерима.

Определение. Неупреждающая функция называется функцией класса , если .

Определение. Неупреждающая функция называется функцией класса 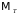, если .

Определение. Функция называется простой, если для конечного разбиения отрезка [0,T] существуют

случайные величины , где -измерима, а -измерима, , такие, что где

Для простых функций стохастический интеграл определяем равенством

и, так как , то

P- п. н.

Для стохастического интеграла от простой функции будем использовать также обозначение .

Очевидно, что

,

где

Отметим, теперь основные свойства стохастических интегралов от простых функций:

1. P- п. н..

2. P- п. н. при

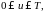
3. - P- п. н. непрерывная по t функция,

4. P- п. н.,

5. P- п. н., где простые функции.

Действительно, так как , то имеем

(9)

Рассмотрим первую сумму правой части равенства (9), в силу свойства K^* условного математического ожидания (смотри §12 главы 1) и свойства iii) винеровского процесса, имеем

.

Поэтому, имеем

(10)

Рассмотрим вторую сумму правой части (9). Воспользуемся опять свойством K^* условного математического ожидания и свойствами винеровского процесса, имеем учитывая, что

Здесь мы учли тот факт, 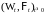является мартингалом относительно меры Р. Значит

. (11)

Таким образом утверждение следует из равенств (9) – (11)

6. Если для всех , то P-п.н. для любого .

7. Процесс 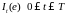- прогрессивно измерим. Это утверждение следует из теоремы 1 главы 3 и, в частности, -измерим при каждом .

8. .

Действительно, из определения стохастического интеграла от простой функции имеем:

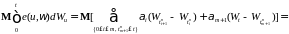
Заметим, что для любого j в силу 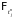-измеримости , имеем

Стохастическое уравнение (определение, существование и единственность сильного решения). Сформулируйте условия существования и единственности сильного решения.

Пусть имеется стохастический базис и - винеровский процесс на нём. Через обозначим измеримое пространство непрерывных функций на со значениями в . Пусть - измеримые функции.

Определение. Будем говорить, что случайный процесс Ито является сильным решением стохастического уравнения

, (22),

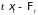если и при каждом - измерим, и Р - п. н. справедливо (22).

В дальнейшем (22) будем называть стохастическим уравнением.

Определение. Будем говорить, что стохастическое уравнение (22) имеет единственное сильное решение, если для любых его двух сильных решений , таких, что , справедливо .

Теорема 34. Пусть выполняются условия:

1) , – измеримые функции;

2) существует константа такая, что для любых :

1. ,

2. ;

3) случайная величина не зависит от и .

Тогда у стохастического уравнения (22) существует единственное сильное решение для любого .

Замечание. Из условия 2) теоремы следует, что коэффициенты стохастического уравнения (22) удовлетворяют условию . Действительно, из условия 2) следует, что

При выполнении каких условий стохастическое уравнение имеет единственное сильное решение (Теорема 34).

Доказательство. Установим сначала единственность сильного решения стохастического уравнения (22). Пусть - два решения стохастического уравнения (22), причём . Тогда очевидно

(23)

Возьмём математическое ожидание относительно левой и правой частей неравенства (22), а затем к первому слагаемому правой части (22 применим неравенство Коши-Буняковского, имеем

(24)

Из свойств стохастических интегралов, условия 2) теоремы и теоремы Фубини, имеем из (22)

.

Отсюда, в силу леммы Гронуолла-Беллмана, следует единственность сильного решения у (22).

При выполнении каких условий решение стохастического уравнения существуют (Теорема 34).

Установим, теперь, существование сильного решения у (22). Для этого воспользуемся методом последовательных приближений. Положим

(25).

Сначала покажем, что для любых 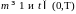существует константа такая, что . Действительно, из (25), в силу замечания из пункта 5.3.1, имеем

. (26) Рассмотрим . В силу (25) и условия Липшица, имеем

(27) где 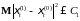. Заметим теперь, что Р - п. н.

Отсюда, в силу леммы 9 и условия 2i), имеем

.

Поэтому ряд

.

Стало быть, в силу леммы Бореля-Кантелли ряд сходится Р - п. н. равномерно по t. Значит последовательность непрерывных процессов Р - п. н. равномерно сходится к непрерывному процессу . Из оценки (26) и леммы Фату следует, что

.

Покажем, что построенный процесс является решением уравнения (22). В соответствии с (25), покажем, что равномерно по t при . Из (23) и (25) имеем Р - п. н.

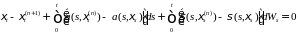. (28).

Заметим, что:

i) в силу условия Липшица, Р - п. н. имеем

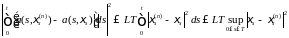, (29).

ii) в силу леммы 10 и условия Липшица, имеем для любых и

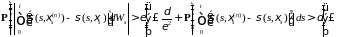
. (30).

Так как , поэтому из (30) и (29) следует, что (28) стремится к 0 по вероятности при равномерно по t. Значит является сильным решением, так как из предыдущих построений следует, что оно - измеримо, где . Доказательство закончено.

(!)Определения марковского процесса, переходной вероятности, переходной вероятности марковского процесса. Докажите, что если стохастическое уравнение имеет единственное сильное решение, то оно является марковским процессом (Теорема 37).

Пусть имеется стохастический базис 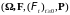. Пусть на стохастическом базисе задан случайный процесс со значениями в , где – польское пространство. Будем считать, что

Определение. Случайный процесс называется марковским, если для 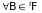, Р – п.н.

(1)

для любого .

Замечание. В силу теоремы Бореля для каждого существуют:

а) измеримый функционал , обозначаемый через , такой, что , следовательно

Р – п.н.

б) измеримая функция , обозначаемая через , такая, что , следовательно Р – п.н.

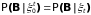причем, в силу (1) Р – п.н. , т.е. Р – п.н.

1.2. Пусть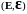 – измеримое пространство, Е – польское (полное сепарабельное метрическое) пространство, .

Определение. Пусть , обозначаемая , такая, что и

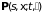1. - при фиксированных – мера;

2. - при фиксированных – измеримая (по Борелю) функция.

Тогда называется переходной вероятностью, или вероятностью перехода.

Гипотеза H₁. Существует семейство переходных вероятностей для марковского процесса со значениями в , такое, что Р – п.н. для любого

(2)

Определение. Если - марковский процесс со значениями в и выполнено (2), то мы будем говорить, что задан марковский процесс с семейством переходных вероятностей .

Предложение 1. Пусть - марковский процесс с семейством переходных вероятностей .Тогда при 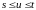справедливо

(3)

где , ((3) называют уравнением Колмогорова–Чепмена).

Доказательство. Доказательство утверждения предложения 1 проводится аналогично доказательству теоремы 1 гл. 2, поэтому его не приводим.

Соглашение H₂: Пусть

Определение. Марковским процессом в широком смысле (МПШ) называется такой процесс, что:

i) принимает значения в ;

ii) – семейство его переходных вероятностей;

iii) выполнены гипотеза Н₁ и соглашение Н₂.

Диффузионные процессы. Достаточные условия того, что марковский процесс является диффузионным (Теорема 38).

Определение. МПШ(марковский процесс в широком смысле) называется диффузионным, если выполняются условия:

i) для любого и 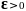vравномерно по , где - сфера радиуса ε с центром в точке x, а ;

ii) существуют вектор-функция и оператор

такие, что для любых и равномерно по

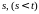
(56),

(57),

при этом 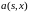n–мерная вектор-функция называется вектором сноса, а b(s,x) матрица-функция размера называется матрицей диффузии.

Будем обозначать через 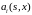i-ую компоненту вектора сноса, а через - элемент матрицы диффузии.

Условия i), ii) неудобны для проверки, поэтому в данном пункте мы приведем достаточные условия того, что процесс диффузионный.