Положим . Очевидно, что из приведенных построений следует, что
(21)
Для любого момента времени t и
, (22)
где
- выходной поток.
Комментарий.
Выше приведенное построение процесса
имеет простую интерпретацию: на вход
системы массового обслуживания (СМО)
поступает поток заявок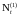
.
Затем, поток обслуженных заявок
прореживается последовательностью
по следующему правилу: если
,
то она поступает на вход системы массового
обслуживания в накопитель необслуженных
заявок, т.е. должна быть обслужена снова,
последнее означает, что обслуживание
произведено некачественно (брак); если
,
то заявка обслужена качественно (не
брак) и она покидает систему массового
обслуживания. Ниже на рис. 2 приведена
структурная схема СМО с обратной связью.
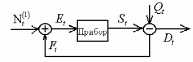
Рис. 2.
Теорема
21.
Пусть
–
простой процесс обслуживания с обратной
связью. Тогда для любого
Р
- п. н. допускает представление:
,
где
и
определяются (20) и (21), соответственно;
(23)
Теорема 22. Уравнение (23) имеет единственное решение для любого
.
Теорема
23. Пусть
точечные процессы
и
не
имеют общих скачков и имеют F
– интенсивности
,
соответственно.
Пусть
–
процесс обслуживания с обратной связью,
описываемый (23), причем
– последовательность бернуллиевских
случайных величин с
,
не зависящая от
,
i=1,2.
Пусть
.
Тогда
удовлетворяет уравнению:
(24)
Доказательство теоремы опирается на утверждение.
Приведите вид компенсаторов для входного, выходного потоков, а также потока обратной связи (Лемма 24).
Лемма
24. Пусть
выполнены условия теоремы 23. Компенсаторы
процессов
,
,
,
относительно потока
и меры P
имеют для
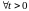вид, соответственно:
.
Доказательство.
Достаточно найти компенсатор для потока
обратной связи
.
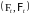Пусть
- предсказуемый ограниченный процесс.
Очевидно, что определен интеграл
Римана-Стилтьеса
и
существует
.
Так как
–
последовательность бернуллиевских
случайных величин, то ясно, что
Отсюда следует утверждение леммы.
Приведите условия существования стационарной очереди (Теорема 25).
Определение.
Пусть
– решение
уравнения (17), если для
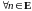существует
,
обозначаемый
,
то его мы будем называть стационарным
решением уравнения
(17).
Для удобства формулировки следующего утверждения приведем условия (R):
для
;
(попутно заметим,
отношение
называют коэффициентом
нагрузки).
Обозначим
.
Теорема
25. Пусть
выполнены условия (R)
и
.
Тогда решение уравнения (17) имеет вид для .
Доказательство.
Рассмотрим пространство последовательностей
,
в нем введем норму:
.
Относительно
этой нормы пространство последовательностей
становится банаховым, которое мы
обозначим через B.
Очевидно, что
,
(для любого t).
Заметим, что любой
,
в силу условий (R),
справедливо равенство
. (26)
Перепишем уравнение (17) в интегральной форме
. (27)
(27) с учетом (26) можно представить в виде
Отсюда следует, что справедливо неравенство
.
Поэтому,
в силу леммы Гронуолла – Беллмана, из
последнего неравенства следует, что
,
т.е.
– решение уравнения (17). Доказательство
закончено.
Какое распределение имеет выходной поток, если входной поток пуассоновский, а очередь стационарна (Теорема 26).