31)Определённый интеграл и его свойства(1-6)

I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. , где х, t – любые буквы.

II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.

III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.

IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

V. Постоянный множитель можно выносить за знак определенного интеграла.

VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.

32)Определённый интеграл и его свойства (7-13)

Физический смысл определенного интеграла:

Путь S, пройденный телом при прямолинейном движении со скоростью v(t) за интервал времени от t1 до t2, вычисляется по формуле

S= v(t)dt

Геометрический смысл определенного интеграла:

Площать S криволинейной трапеции (фируры, ограниченной графиком непрерывной положительной на интервале (a;b )функции y=f(x), осью OX и прямыми x = a и x = b) вычисляется по формуле

S=f(x)dx

33)Вычисление определённого интеграла формулой Ньютона-Лейбница

Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.

Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x) , вычислить ее значения в точках a и b и найти разность F(b) – F(a).

Примеры

34)Интегрирование по частям и замена переменной в определённом интеграле

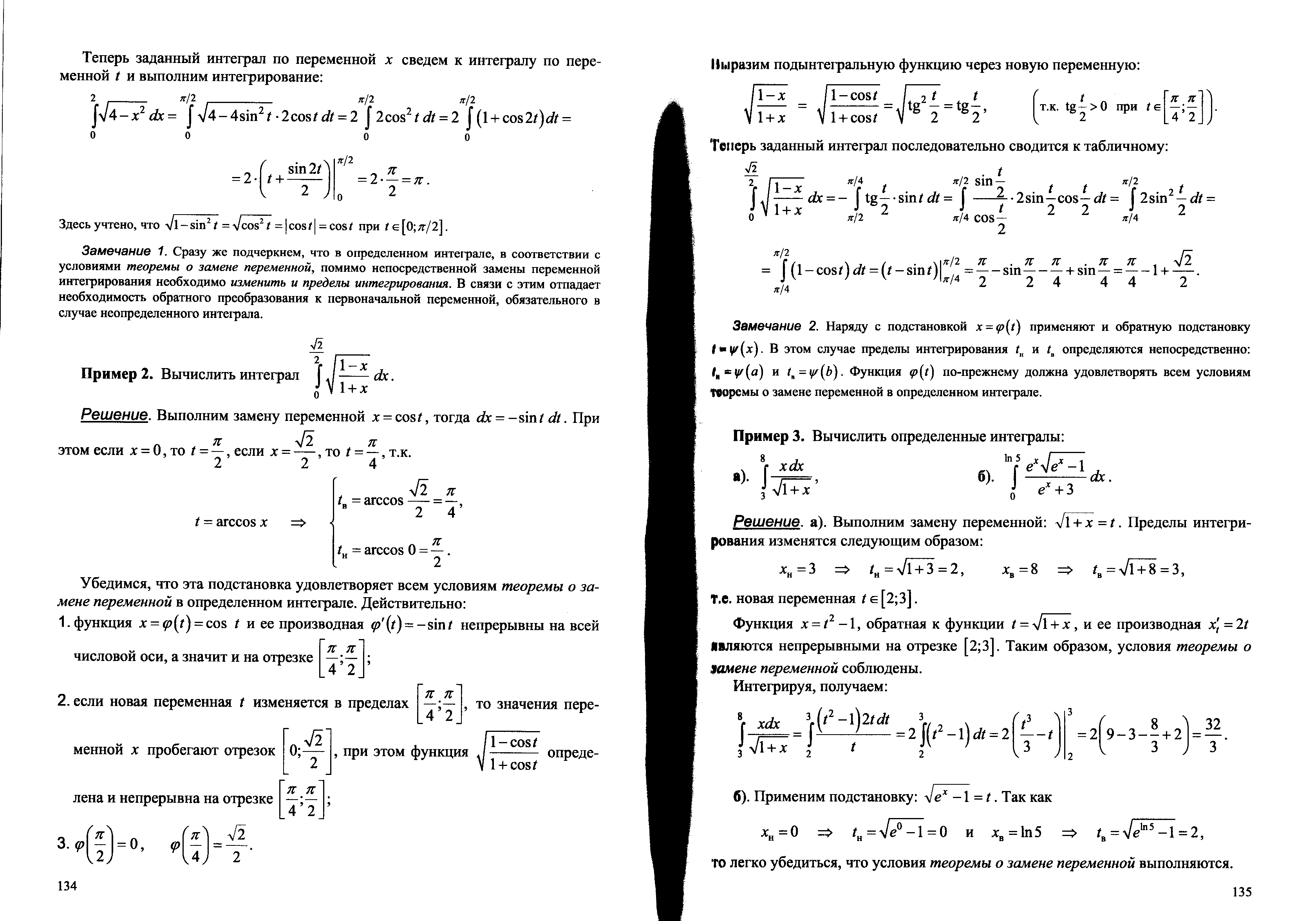
35)Приложения определённого интеграла

-Вычисление фигур заданных в параметрическом виде: Пусть границами криволинейной трапеции являются прямые x = a, x = b, ось абсцисс и параметрически заданная кривая , причем функции и непрерывны на интервале , монотонно возрастает на нем и .

Тогда площадь криволинейной трапеции находится по формуле .

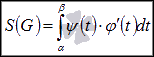
-Вычисление в полярной системе:

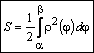
-Вычисление в декартовой системе:

S=F(b)-F(a).

-Вычисление длины дуги плоской кривой:

А)в декартовой

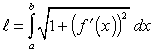
Б) в параметрическом виде

x', y' и z' – производные функций x(t), y(t) и z(t) по переменной t.

Тогда или

В)в полярном

-Вычисление объёма

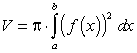
36)Дифференциальные уравнения .Основные определения.

1) Определение (понятие) дифференциального уравнения. уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке.

2) Определение (понятие) обыкновенного дифференциального уравнения. Если искомая функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным.

3) Определение (понятие) обыкновенное дифференциальное уравнение порядка "n" имеет следующий вид:

F(x,y,y',y'',..,y(n))=0

Следовательно, диффернциальное уравнение первого порядка имеет вид

F(x,y,y')=0

Здесь F известная функция от "n+2" переменных, удовлетворяющая определенным условиям непрерывности, дифференцируемости, а y=y(x) - функция, которую надо найти.

Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.

4) Определение (понятие) решения (не общего) дифференциального уравнения на интервале (a,b) называется функция, имеющая на этом интервале производные y,y',y'',..,y(n) и удовлетворяющая для всех х∈ (a,b) уравнению.

График решения обыкновенного дифференциального уравнения называется интегральной кривой этого уравнения.

5)Определение (понятие) общего решения дифференциального уравнения

Общее решение содержит все решения уравнения. Общее решение уравнения n-го порядка содержит "n" произвольных постоянных и имеет вид y=φ(x, c1, c2,..,cn)

Если соотношение, связывающее x, y и "n" произвольных постоянных, дано в виде, не разрешенном относительно y:

φ(x,y,c1, c2,..,cn )=0, (квазиобщее решение) это будем называть такое соотношение общим интегралом уравнения.

Процесс нахождения решений уравнения называется интегрированием дифференциального уравнения.

6) Задача Коши(нахождение частного решения.Нахождение С и его подстановка).

Задача Коши состоит в отыскании решения уравнения F(x,y,y',y'',..,y(n))=0, удовлетворяющего условиям при x=xo , y(xo)=yo ...... y(n-1)(xo)=y(n-1)o - граничные (начальные условия задачи Коши), где xo ,yo , y1o, y2o,...,y(n-1)o, - заданные числа. Другими словами задача Коши состоит в нахождении такого решения, которое удовлетворяет начальным условиям. Любая реальная задача - задача Коши. Решение уравнения в общем виде не является решением задачи Коши.

7) Определение (понятие) уравнения с частными производными. Если искомая функция "z" зависит от нескольких независимых переменных x1 ,х2 ,.., хn (n≥2), то уравнение называется уравнением с частными производными. При n=2, уравнение имеет вид:,

здесь F - заданная функция.z(x1,x2) - искомая функция.

8)Уравнение Бирнулли

В общем случае, когда m ≠ 0, 1, уравнение Бернулли сводится к линейному дифференциальному уравнению с помощью подстановки

Новое дифференциальное уравнение для функции z(x) имеет вид

и может быть решено способами, описанными на странице Линейные дифференциальные уравнения первого порядка.

Гораздо проще не сводить уравнение Бернулли к линейному, а искать решение в виде y=uv , то есть использовать метод Бернулли.А затем составить систему.Решив одно уравнение системы можно подставить значение во второе.