7.Общее исследование функции.

Исследование функции у=ƒ(х) целесообразно вести в определенной последовательности.

1. Найти область определения функции.

2. Найти (если это можно) точки пересечения графика с осями координат.

3. Выяснить, является ли функция четной, нечетной или общего вида.

4. Найти асимптоты графика функции.

5. Найти интервалы монотонности функции.

6. Найти экстремумы функции.

7. Найти интервалы выпуклости и точки перегиба графика функции. На основании проведенного исследования построить график функции.

8.Комплексные числа. Определение и алгебраическая форма.

Комплексным числом z называется выражение вида z=х+iу, где х и у — действительные числа, a i — так называемая мнимая единица, i2=-1.

Если x=0, то число 0+iy=iy называется чисто мнимым; если у=0, то число х+i0=х отождествляется с действительным числом х, а это означает, что множество R всех действительных чисел является подмножеством множества С всех комплексных чисел, т. e. RÌС.

Число х называется действительной частью комплексного числа z и обозначается х=Re z, а у — мнимой чαстпъю z, у = Im z.

Два комплексных числа z1=x1+iy1 и z2=х2+iy2 называются равными (z1=z2) тогда и только тогда, когда равны их действительные части и равны их мнимые части: х1=х2, y1=у2. В частности, комплексное число z=х+iy равно нулю тогда и только тогда, когда х=у=0. Понятия «больше» и «меньше» для комплексных чисел не вводятся.

Два комплексных числа z=х+iy и z=х-iy, отличающиеся лишь знаком мнимой части, называются сопряженными.

Запись числа z в виде z=х+iy называют алгебраической формой комплексного числа.

9.Тригонометрическая форма комплексного числа.

Модуль r и аргумент φ комплексного числа можно рассматривать как полярные координаты вектора r=ОМ, изображающего комплексное числоz=х+iy Тогда получаем х=rcosφ, у=rsinφ. Следовательно, комплексное число z=х+iy можно записать в виде z=rcosφ+irsinφ или z=r(cosφ+i sinφ).

Такая запись комплексного числа называется тригонометрической формой.

10.Умножение и деление комплексных чисел в тригонометрической форме. Теорема.

Теорема 1. Модуль произведения двух комплексных чисел равен произведению их модулей, а аргумент — сумме их аргументов.

Теорема 2. Модуль частного двух комплексных чисел равен частному модулей делимого и делителя; аргумент частного двух не равных нулю комплексных чисел равен разности аргументов делимого и делителя.

11.Возведение в степень комплексного числа.

Операцию возведения в степень удобнее выполнять, когда комплексное число записано в тригонометрической или в показательной форме.

Для возведения комплексного числа в степень нужно модуль возвысить в эту степень, а аргумент умножить на показатель степени.

12.Корень н-ой степени из комплексного числа. Формула Муавра.

Эта формула позволяет возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:

где r— модуль, а — аргумент комплексного числа. Приведенная формуле справедлива при любом целом n, не обязательно положительном.

Аналогичная формула применима также и при вычислении корней -ой степени из ненулевого комплексного числа:

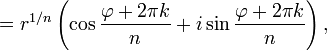
Отметим, что корни -й степени из ненулевого комплексного числа всегда существуют, и их количество равно . На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного -угольника, вписанного в окружность радиуса с центром в начале координат