13. Многочлены и дробно-рациональные функции.

Функции вида f(x)=p(x)/q(x), где p и q - многочлены, называют дробно-рациональными функциями.

Функция вида Рn(х)= aохn+a1xn-l+• • •+аn-1х+аn ,где n - натуральное число, αi (i=0,1,.., n) - постоянные коэффициенты, называется многочленом (или целой рациональной функцией). Число n называется степенью многочлена. Корнем многочлена называется такое значение х0 (вообще говоря, комплексное) переменной х, при котором многочлен обpaщaeтcя в нуль, т. е. Рn(хо)=0.

Теорема. Если х1 есть корень многочлена Рn(х), то многочлен делится без остатка на х-х1, т. е. Pn(x)=(x-x1)*Pn -1(x),где Рn-1(х) - многочлен степени (n-1).

Теорема .Всякий многочлен Рn(х) можно представить в виде Рn(x)= αо(х-х1)(х-х2)... (х-хn), где х1, х2,...,хn - корни многочлена, αо - коэффициент многочлена при хn.

Теорема .Если многочлен Рn(х)=aoxN+a1xN-1+• • •+an тождественно равен нулю, то все его коэффициенты равны нулю.

Теорема .Если два многочлена тождественно равны друг другу, то коэффициенты одного многочлена равны cоотвeтcтвyющим коэффициентам другого.

Теорема .Если многочлен Рn(х) с действительными коэффициентами имеет комплексный корень α+ib, то он имеет и сопряженный корень α-ib.

Дробно-рациональной функцией (или рациональной дробью) называется функция, равная отношению двух многочленов, т. е. ƒ(х) = , где Рm(х) - многочлен степени т, а Qn(x) - многочлен степени n.

Рациональная дpобь называется правильной если степень числителя меньше степени знаменателя, т. е. m<n; в противном случае (если т ип ) рациональная дробь называется неправильной.

Всякую неправильную рациональную дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби, т. е.

14.Разложение правильной дроби в сумму простейших.

Различают следующие виды простейших дробей:

1.

2.

3.

4.

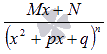
Пример. Разложить дробь на простейшие.

Решение.

Вообще отношение многочленов раскладывают на простейшие дроби, если степень многочлена числителя меньше степени многочлена в знаменателе. В противном случае сначала проводят деление многочлена числителя на многочлен знаменателя, а уже затем проводят разложение правильной дробно рациональной функции.

Выполним деление столбиком (уголком):

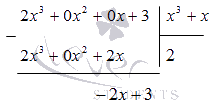
Следовательно, исходная дробь примет вид:

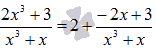
Таким образом, на простейшие дроби будем раскладывать

Во-первых, раскладываем знаменатель на множители.

Во-вторых, раскладываемую дробь представляем в виде суммы простейших дробей с неопределенными коэффициентами.

В-третьих, приводим полученную сумму простейших дробей с неопределенными коэффициентами к общему знаменателю и группируем в числителе слагаемые при одинаковых степенях х.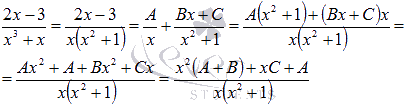

То есть, пришли к равенству: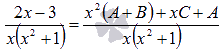

При x отличных от нуля это равенство сводится к равенству двух многочленов

А два многочлена являются равными тогда и только тогда, когда коэффициенты при одинаковых степенях совпадают.

В-четвертых, приравниваем коэффициенты при одинаковых степенях х.

При этом получаем систему линейных алгебраических уравнений с неопределенными коэффициентами в качестве неизвестных: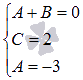

В-пятых, решаем полученную систему уравнений любым способом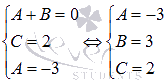

В-шестых, записываем ответ.