1.Теоремы о непрерывных функциях на [a,b]

1.Т. Вейерштрасса

Пусть f(x) задана на интервале [a,b] и непрерывна в [a,b] тогда f(x) ограничена в этом замкнутом интервале.

2.Т. Вейерштрассе

f(x) непрерывна в [a,b] тогда в этом интервале она принимает свое самое большое и малое значения.

Найдется точка х принадлежащая [a,b]

f(x)=inf f(x)-самое малое значение(инфиум)

f(x)=sup f(x)-самое большое значение(супрэмум)

3.Т. Больцано — Коши

f(x) непрерывна на [a,b], и на концах принимает значения разных знаков ,тогда внутри отрезка [a, b] найдется, по крайней мере, одна точка x = C, в которой функция обращается в ноль: f(C) = 0, где a < C< b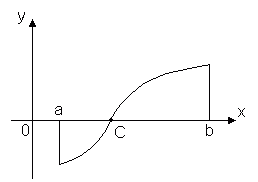

4.Т.о промежуточных значениях

Пусть функцияy = f(x) непрерывна на отрезке [a, b] и f(a) = A, f(b) = B. (А неравно В)Тогда функция f(x) в промежутке [a,b] принимает все промежуточные значения между А и В.

2.Основные теоремы дифференциального исчисления. Т Ферма и Ролля.

1.Т. Ферма

Пусть функция y = f(x) определена в интервале (а, в) и принимает в точке с этого интервала наибольшее или наименьшее на (а, в) значение. Если существует f'(с), то f'(с) = 0.

2.Т. Ролль

Если функция f(x) непрерывна на отрезке [a,b] ,дифференцируема на интервале (a,b) и на концах отрезка принимает одинаковые значения f(а)= f(b), то найдется хотя бы одна точка с є (a,b), в котором производная f’(x) обращается в нуль, т.е. f’(с)=о

3.Теоремы Лагранжа и Коши

1. Т. Лагранжа

Пусть функция y=f(x) непрерывна на отрезке [a, b] и дифференцируема в интервале (a, b). Тогда существует хотя бы одна точка с є (a, b), для которой выполняется условие:

2.Т.Коши

Если функции ƒ(х) и φ(x) непрерывны на отрезке [a;b], дифференцируемы на интервале (α;b), причем φ'(х) неравно 0 для хє(а;b), то найдется хотя бы одна точка с є(a;b) такая, что выполняется равенство

4.Монотонность и экстремумы. Теорема

5.Выпуклость и точки перегиба. Теоремы.

Функция называется выпуклой к верху на некотором множестве, если её график лежит ниже касательной.

Точка отделяющая выпуклый участок от вогнутого, называется точкой перегиба.

Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый.

Теорема (достаточное условие существования точек перегиба). Если вторая производная ƒ"(х) при переходе через точку х0, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой х0 есть точка перегиба.

6.Асимптоты. Теорема о нахождении правой и левой асимптоты.

Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки до кривой.

Асимптоты могут быть вертикальными, наклонными(горизонтальные)

Вертикальная

Вертикальная асимптота — прямая вида при условии существования предела .

Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

Горизонтальная

Горизонтальная асимптота — прямая вида при условии существования предела

Наклонная

Наклонная асимптота — прямая вида при условии существования пределов