10.1Критические точки функции. Необходимое условие экстремума.

Мы рассмотрели поведение функции на промежутках, где f(х)>0 и f'(х)<0. Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками этой функции. Эти точки играют важную роль при построении графика функции, поскольку только они могут быть точками экстремума функции (рис. 1 и 2). Сформулируем соответствующее утверждение, его называют теоремой Ферма (в честь французского математика Пьера Ферма).

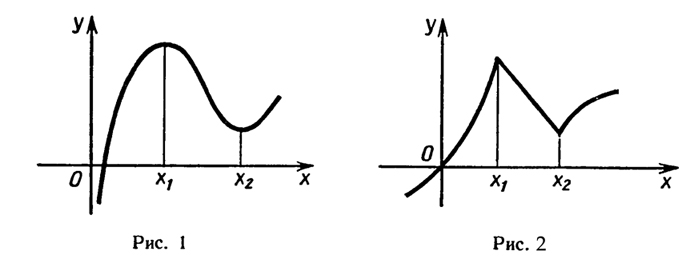
Необходимое условие экстремума. Если точка хо является точкой экстремума функции f и в этой точке существует производная f’, то она равна нулю:F’(x0) =0.

Рассмотрим случай f'(x0)>0. По определению производной отношение при х→х0 стремится к положительному числу f' (х0), а следовательно, и само будет положительно при всех х, достаточно близких к x0. Для таких х

и, значит, f(x)>f(x0) для всех х>х0 из некоторой окрестности точки x0. Поэтому х0 не является точкой максимума.

Если же х<х0, то f (x)<f(x0), и, следовательно, х0 не может быть и точкой минимума f.

Случай F'(x0)<0 разбирается аналогично.

Важно отметить, что теорема Ферма есть лишь необходимое условие экстремума: из того, что производная в точке хо обращается в нуль, необязательно следует, что в этой точке функция имеет экстремум. Например, производная функции f(х)=х3 обращается в нуль в точке 0, но экстремума в этой точке функция не имеет (рис. 3).

До сих пор мы рассматривали критические точки, в которых производная равна нулю. Рассмотрим теперь критические точки, в которых производная не существует. (Отметим, что, например, точка 0 для функции не является критической: в ней производная не существует, но она не внутренняя точка области определения.) В этих точках функция также может иметь или не иметь экстремум.

11. Достаточное условие экстремума

Теорема. Пусть функция f (x) непрерывна в некотором интервале, содержащую точку экстремума х1, и дифференцируема во всех точках этого интервала кроме, быть может самой точки х1. Если при переходе слева направо через эту точку х1 производная меняет знак с плюса на минус, то при х = х1 функция имеет локальный максимум. Если же при переходе слева направо через эту точку х1 производная меняет знак с минуса на плюс, то функция имеет в этой точке локальный минимум.

Комментарий. Если в достаточно малой окрестности точки х1 справедливо f ' (x) > 0 при х < x1, f ' (x) < 0 при х > x1, то в точке х1 функция имеет максимум; если f ' (x) < 0 при х < x1, f ' (x) > 0 при х > x1, то в точке х1 функция имеет минимум.

Доказательство. Пусть при переходе слева направо через эту точку х1 производная меняет знак с плюса на минус, то есть для всех х, достаточно близких к х1, имеем f ' (x) > 0 при х < x1, f ' (x) < 0 при х > x1. Применяя теорему Лагранжа к разности f (x) − f ( x1), получим

f ( x ) − f ( x1 ) = f ' ( c )·( x − x1 ).

где с лежит между точками х и х1. По условию теоремы

sign f ' ( c ) = − sign ( x − x1 ),

поэтому в произвольно малой окрестности точки х1 имеем

f ( x ) < f ( x1 ).

В этом случае точка х1 есть точка локального максимума, что и требовалось доказать.