3.Полный дифференциал

Полный дифференциал, функции f (x, у, z,...) нескольких независимых переменных — выражение

в случае, когда оно отличается от полного приращения

Df = f (x + Dx, y + Dy, z + Dz,…) - f (x, y, z, …)

на величину, бесконечно малую по сравнению с

4. Производная сложной функции.

Функции сложного вида не совсем корректно называть термином «сложная функция». К примеру, 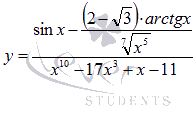смотрится очень внушительно, но сложной эта функция не является, в отличие от .

В этой статье мы разберемся с понятием сложной функции, научимся выявлять ее в составе элементарных функций, дадим формулу нахождения ее производной и подробно рассмотрим решение характерных примеров.

При решении примеров будем постоянно использовать таблицу производных и правила дифференцирования, так что держите их перед глазами.

Сложная функция – это функция, аргументом которой также является функция.

С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать как f(g(x)). То есть, g(x) как бы аргумент функции f(g(x)).

К примеру, пусть f – функция арктангенса, а g(x) = lnx есть функция натурального логарифма, тогда сложная функция f(g(x)) представляет собой arctg(lnx). Еще пример: f – функция возведения в четвертую степень, а - целая рациональная функция (смотрите классификацию элементарных функций), тогда .В свою очередь, g(x) также может быть сложной функцией. Например, . Условно такое выражение можно обозначить как . Здесь f – функция синуса, - функция извлечения квадратного корня - дробная рациональная функция. Логично предположить, что степень вложенности функций может быть любым конечным натуральным числом .

Часто можно слышать, что сложную функцию называют композицией функций.

Формула нахождения производной сложной функции.

Пример.

Найти производную сложной функции .

Решение.

В данном примере f – функция возведения в квадрат, а g(x) = 2x+1 – линейная функция.

Вот подробное решение с использованием формулы производной сложной функции:

Давайте найдем эту производную, предварительно упростив вид исходной функции.

Следовательно,

Как видите, результаты совпадают.

Постарайтесь не путать, какая функция есть f, а какая g(x).

Поясним это примером на внимательность.

Инвариантность формы полного дифференциала

Выражение полного дифференциала функции нескольких переменных имеет тот же вид вне зависимости от того, являются ли u и v независимыми переменными или функциями других независимых переменных.

Доказательство опирается на формулу полного дифференциала

Что и требовалось доказать.

5.Полная производная функции — производная функции по времени вдоль траектории. Пусть функция имеет вид и ее аргументы зависят от времени: . Тогда , где — параметры задающие траекторию. Полная производная функции (в точке ) в таком случае равна частной производной по времени (в соответствующей точке ) и может быть вычислена по формуле:

,

где — частные производные. Следует отметить, что обозначение является условным и не имеет отношения к делению дифференциалов. Кроме того, полная производная функции зависит не только от самой функции, но и от траектории.

Например, полная производная функции :

Здесь нет так как сама по себе («явно») не зависит от .

Полный дифференциал

Перевод