22. Длина дуги кривой.

Пусть задана кривая Тогда длина ее участка, ограниченного значениями t = α и t = β выражается формулой

В частности, длина плоской кривой, задаваемой на координатной плоскости OXY уравнением y = f (x), a ≤ x ≤ b, выражается формулой

23. Вычисление объема тела по площадям его параллельных сечений

Рассмотрим тело D, ограниченное плоскостями х = а и х = b (рис. 247).

Через S(x) обозначим площадь сечения тела D плоскостью, проходящей через точку с абсциссой х [а; b] и перпендикулярной оси Ох. Будем предполагать, что

1) функция S(x) непрерывна на [а; b];

2) для любых x1 и x2 из [а; b] сечения тела D плоскостями х = x1 и х = x1 таковы, что одно из них проектируется в другое.

Тело D, обладающее этими свойствами, будем называть телом с допустимыми параллельными сечениями.

Теорема. Объем тела с допустимыми параллельными сечениями вычисляется по формуле

Отрезок [а; b] точками

разобьем на п отрезков [хi—1 ; хi] длины

Пусть тi и Mi — наименьшее и наибольшее значения функции S(x) на отрезке

[хi—1 ; хi] .

Плоскостями х = хi, где i = 1, 2, ..., п — 1, тело D разобьем на n слоев. Выделим i-й слой, соответствующий отрезку [хi—1 ; хi], и построим два цилиндра высрты Δ хi :

один с основанием площади Mi , содержащий i-й слой, а другой с основанием площади тi , содержащийся в i-м слое (рис. 248).

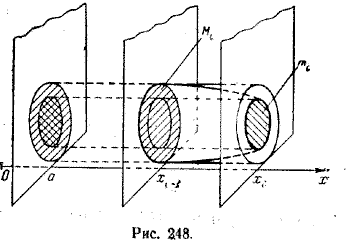
Объемы этих цилиндров равны Mi Δ хi и тi Δ хi.

Произведя указанные построения для каждого слоя, получим два ступенчатых тела D'n и D"n таких, что D'n < D < D''n.

Их объемы равны

Так как функция S(x) непрерывна, то V'n и V"n при п —> ∞ имеют один и тот же предел, равный .

Следовательно, объем тела D вычисляется по формуле (1).

Замечание. Можно доказать, что формула (1) остается справедливой и в том случае, когда условие 2) для тела D не выполняется.

Задача. Определить объем тела, отсекаемого от прямого кругового цилиндра плоскостью, проходящей через диаметр основания и составляющей с плоскостью основания угол α (α < 90°). Радиус основания цилиндра равен R.

Введем систему координат так, как показано на рис. 249, и рассмотрим сечения данного тела плоскостями, перпендикулярными оси Оx.

Вычислим площадь сечения плоскостью, проходящей через точку А с абсциссой х,

|х| < R. Это сечение представляет собой прямоугольный треугольник ABC, и поэтому

24. Объем тела вращения.

Пусть тело образовано вращением вокруг оси OX криволинейной трапеции, ограниченной непрерывной на отрезке [a; b] функцией f (x). Его объем выражается формулой

Пусть тело заключено между плоскостями x = a и x = b, а площадь его сечения плоскостью, проходящей через точку x, – непрерывная на отрезке [a; b] функция σ (x). Тогда его объем равен

25. Геометрическое и механическое приложения определенного интеграла

Если на отрезке [a,b] задана функция f(x)≥0, то, как известно из определения определенного интеграла, он определяет площадь криволинейной трапеции, ограниченной линиями y=f(x), осью ОХ и прямыми x=a, x=b; т.е.

Если же функция f(x)≤0 на интервале [a, b], то и определенный интеграл также ≤0. Но по абсолютной величине определенный интеграл равен площади S соответствующей криволинейной трапеции

Если функция y=f(x) конечное число раз меняет знак на отрезке [a,b], то интеграл по всему отрезку [a,b] разбиваем по частичным отрезкам.

Интеграл будет положителен на тех отрезках, где f(x) , и отрицателен там где f(x) . Таким образом, интеграл по всему отрезку даст разность площадей, лежащих выше и ниже оси ОХ.

Для того, чтобы получить сумму площадей в обычном смысле, нужно найти сумму абсолютных величин интегралов по указанным выше отрезкам и вычислить интеграл.

Пример 1.

Вычислить площадь S, ограниченную синусоидой y=sinx и осью ОХ, при 0 .

Решение:

т.к. sinx , при 0 и sinx при , то имеем

Следовательно, кв.ед.

Если нужно вычислить площадь, ограниченную кривыми y=f1(x) и y=f2(x) и ординатами x=a и х=b, при условии, что f1(x) f2(x) будем, очевидно, иметь.