17. Лнду с ПостК и спч вида . Метод неопределенных коэффициентов. Метод комплексных амплитуд.

- ЛНДУ n-го порядка. (1)

В общем случае специальная правая часть выглядит как (2). Что-то из этого может отсутствовать.

Т.: общее решение уравнения (1) с СПЧ (2) всегда может быть получено в элементарных функциях: . следует искать в виде (3), где , - многочлены степени l с неопределенными коэффициентами, , если - корень кратности , и , если - не корень. После подстановки (3) в (1) и сокращения на , приравниваются коэффициенты при одинаковых степенях и , и отдельно. Коэффициенты всегда можно найти и притом единственным образом.

Пусть СПЧ имеет вид , .

, .

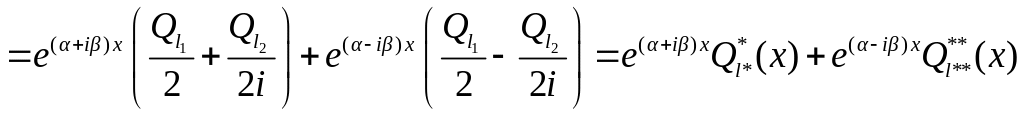
а) - не корень

Используя принцип суперпозиции, будем искать ЧР в виде . Можно показать, что если , то . Подставим в ЧР:

б) - корень кратности

Если один из многочленов есть тождественный ноль, то легче искать частное решение методом комплексных амплитуд.

Если , то перейдем к вспомогательному уравнению , , где - многочлен с неопределенными коэффициентами. .

Если , то проделаем все то же самое, только

18. Гармонический осциллятор под действием внешней гармонической силы. Явление резонанса.

.

, найдем ЧР методом комплексных амплитуд.

а) , тогда не корень, и , , . Подставим в уравнение, получим: . Тогда ,

, где первое слагаемое отвечает собственным колебаниям, а второе – вынужденным.

Результирующее движение – суперпозиция собственных колебаний системы с собственной частотой и вынужденных колебаний частоты внешней силы.

б) , тогда корень, , , , , . Подставим в уравнение, получим . Тогда ,

.

Амплитуда вынужденных колебаний становится переменной и неограниченно растет с течением времени. Это явление резонанса, имеющее место при совпадении собственной частоты системы и частоты внешней силы. В астрономии выражение, имеющее вид произведения периодической функции на степень независимой переменной называется вековым членом.

19. Линейный осциллятор под действием внешней гармонической силы.

20. Лоду n-го порядка с ПеремК. Приведение к лду с ПостК с помощью замены аргумента.

- ЛОДУ с переменными коэффициентами (1). Коэффициенты и правая часть определены и непрерывны на . Общее решение: . Рассмотри однородное уравнение: (2). В случае не существует общих способов построения ФСР.

Т.: линейность и однородность уравнения (2) сохраняются при замене независимой переменной , где - любая n раз дифференцируемая функция, причем .

Т. (необходимое условие приводимости (2) к ЛДУ с постоянными коэффициентами): если (2) может быть приведено к ЛДУ с постоянными коэффициентами при помощи замены независимой переменной, то только формулой вида: .

Существует только один класс уравнений – уравнения Эйлера, приводимые к ЛДУ с постоянными коэффициентами такой заменой. В остальных случаях метод неприменим.

21. Оду Эйлера.

(1) – однородное уравнение Эйлера.

Т.: однородное уравнение Эйлера всегда приводится к ЛДУ с постоянными коэффициентами заменой .

Доказательство: , 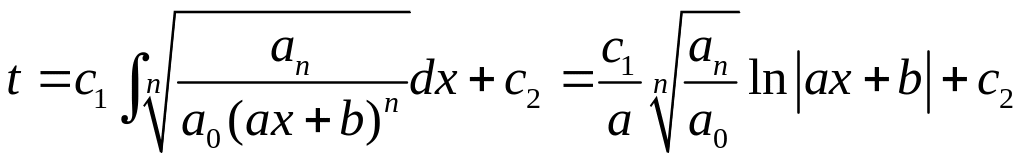необходимое условие выполнено, покажем, что уравнение с постоянными коэффициентами:

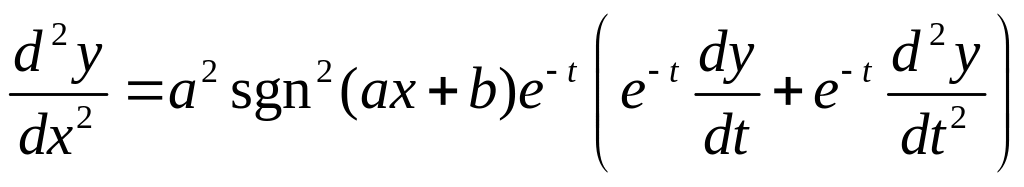
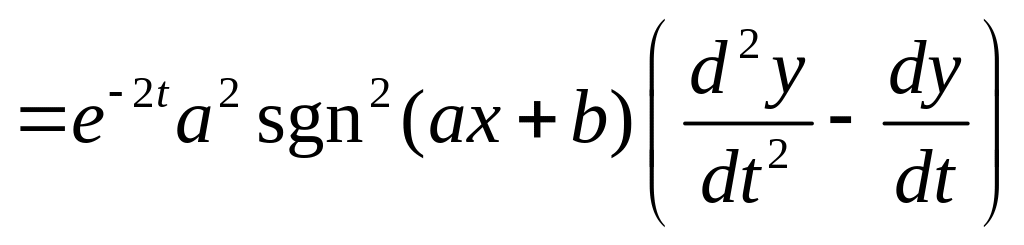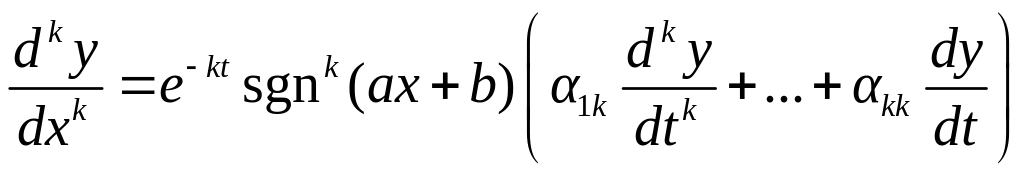, , , , , . Подставим в (1), получим .

Т.к. сигнум входит в четной степени, общее решение не зависит от знака . Поэтому достаточно найти решение при , сделав замену , а затем заменить: , .