37. Лнсду. Т. О структуре общего решения. Некоторые свойства решений. Принцип суперпозиции.
- (1) ЛНСДУ
Т. о структуре общего решения:
Доказательство: пусть известно частное
решение
.
Сделаем замену
,
тогда
.
Подставим в (1):
.
должно быть решением соответствующей
однородной системы. Пусть
- ФСР соответствующей однородной системы,
докажем, что
(2) – решение неоднородной. При любом
наборе коэффициентов это выражение
является решением (1). Т.к. система (1) для
любого набора конечных начальных условий
имеет единственное решение, то достаточно
показать, что из (2) можно выделить частное
решение подбором
.
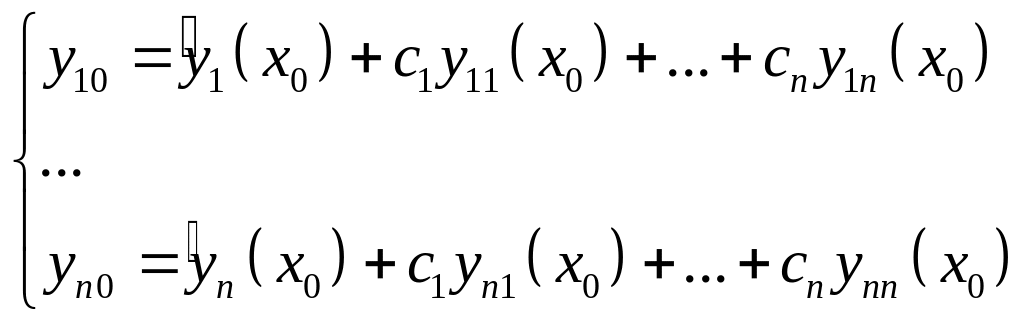- относительно
это линейная неоднородная алгебраическая
система с определителем, равным
вронскиану, т.е. отличным от 0, следовательно,
она имеет единственное решение.
Свойства решений:
Принцип суперпозиции. Если
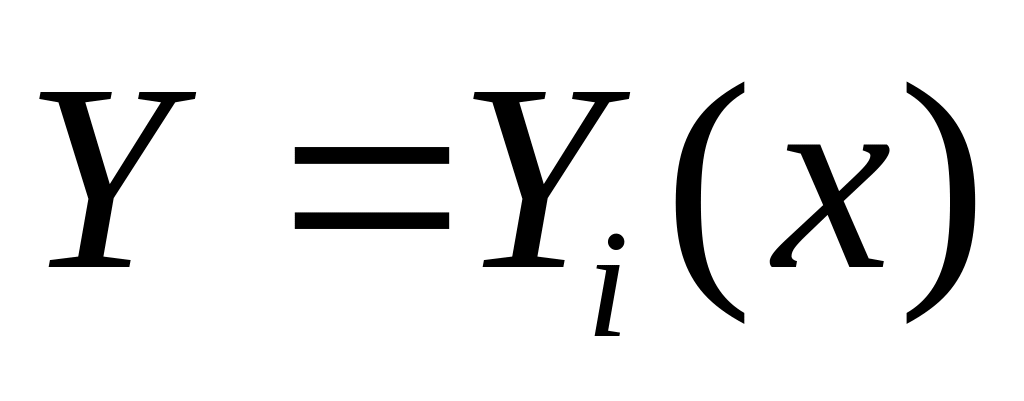- решение линейной неоднородной системы
,
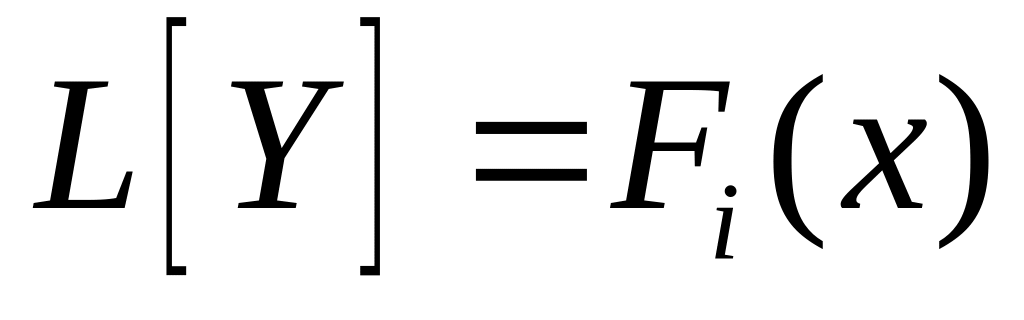то
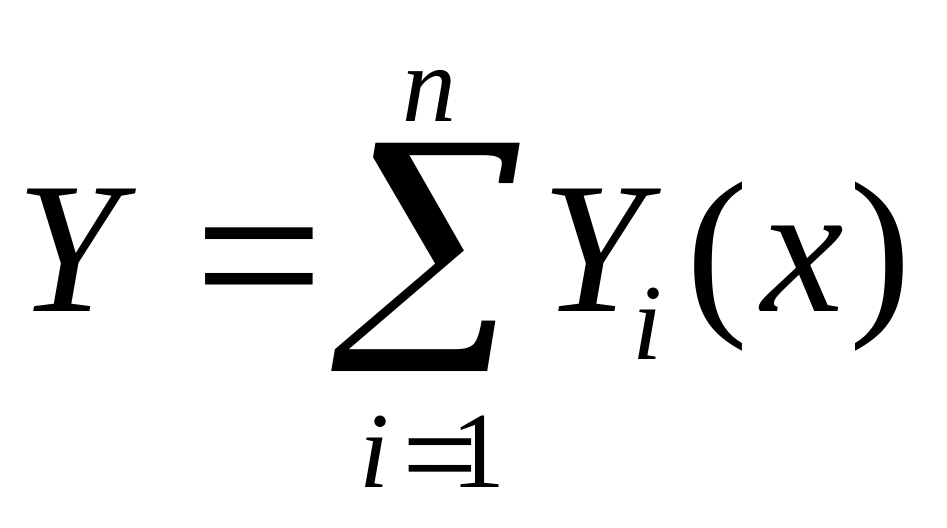- решение
.
Доказательство: рассмотрим
Если система
,
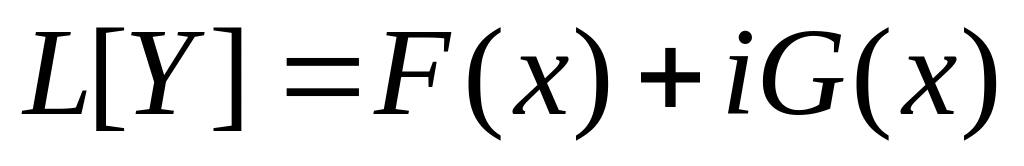где
,
,
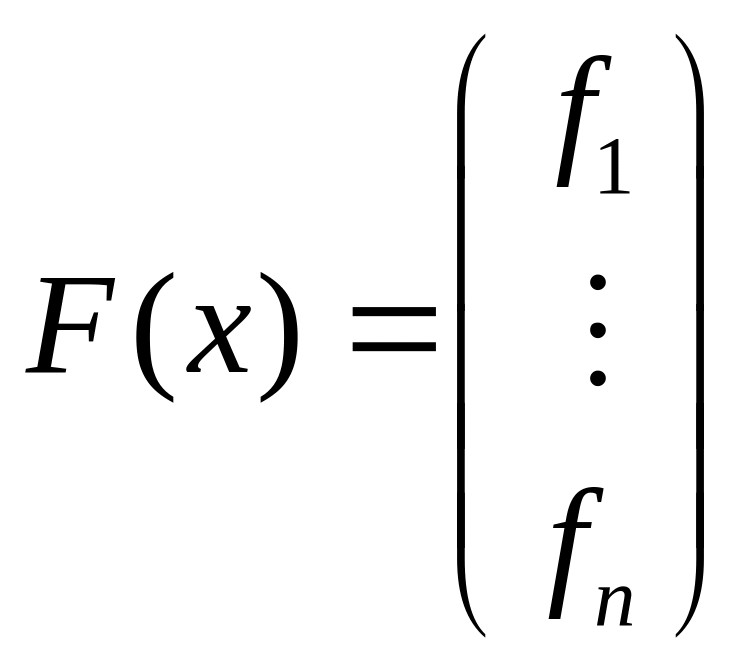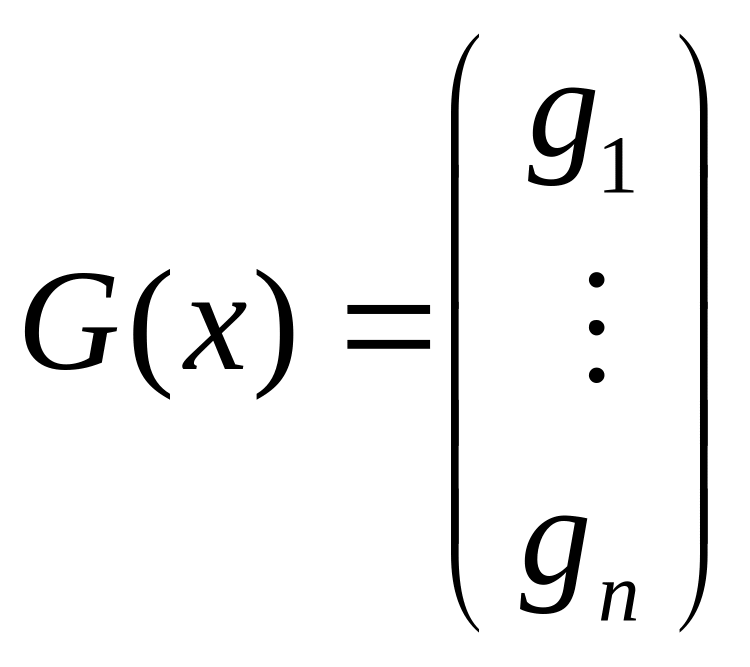а все коэффициенты
,
,
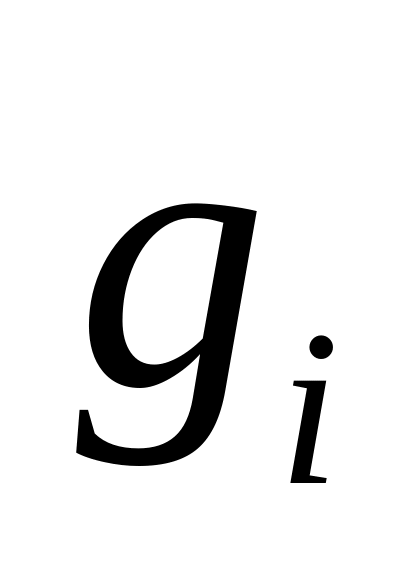действительны, то система имеет решение
,
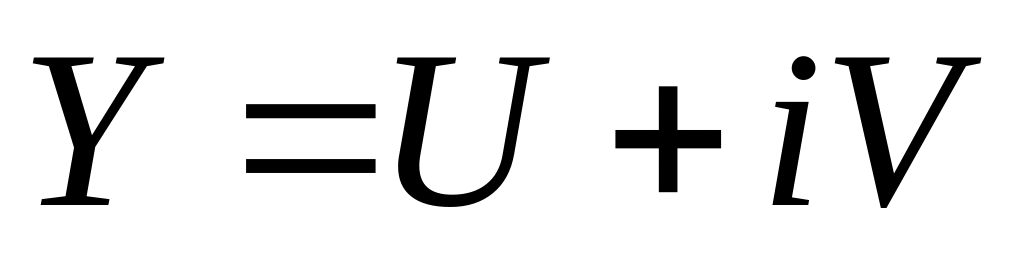где
,
,
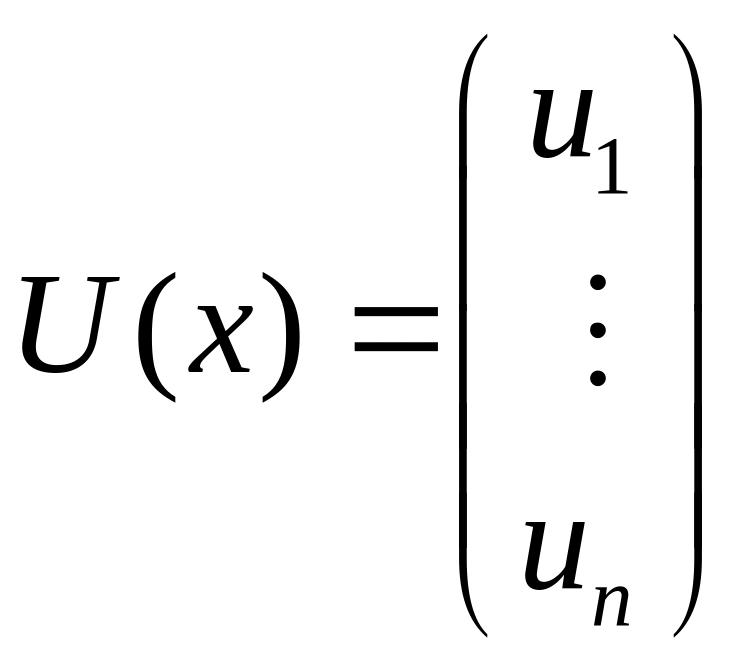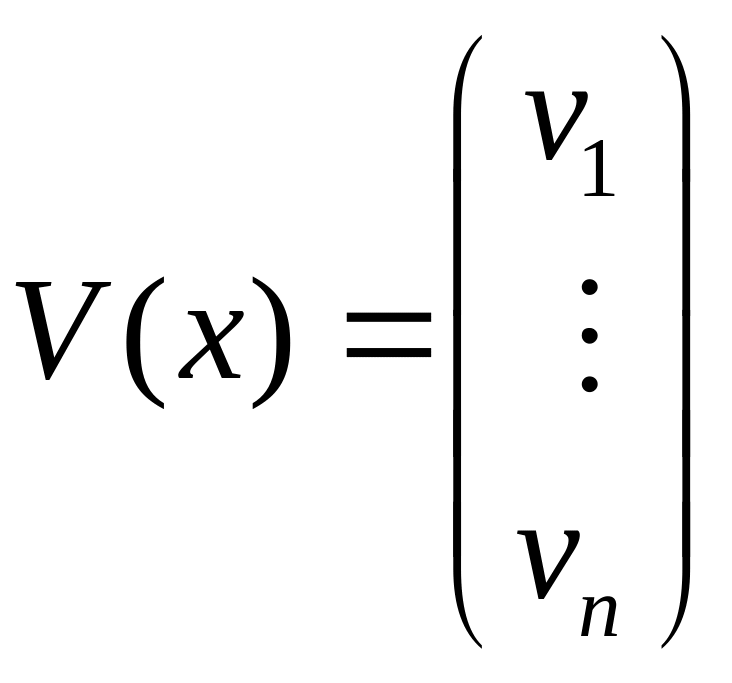и функции
,
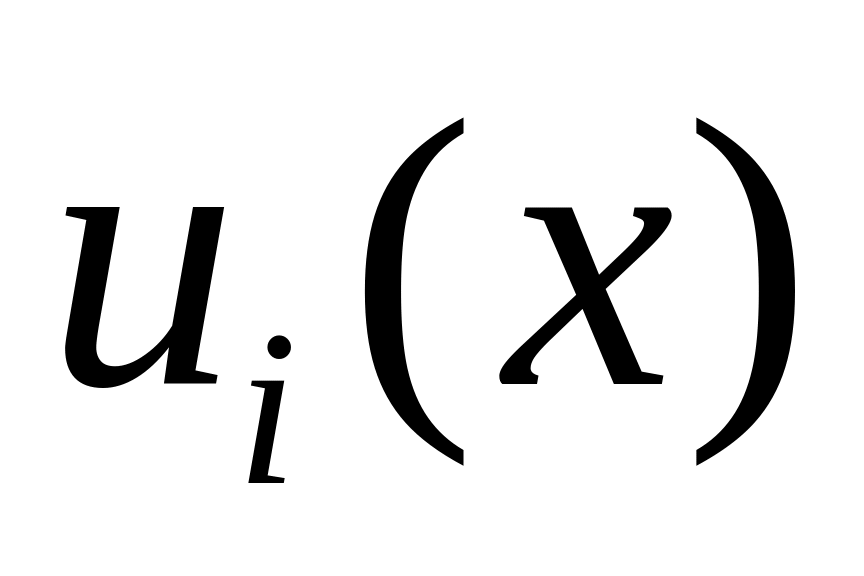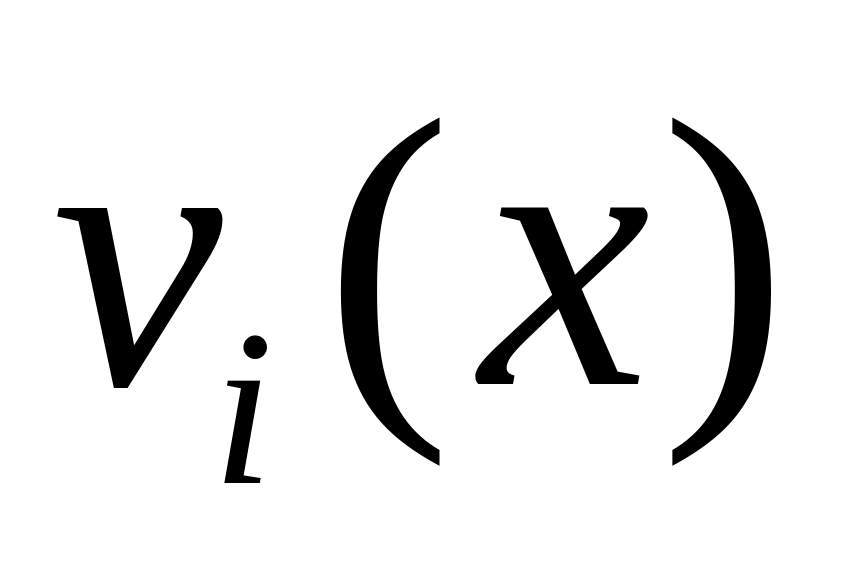действительные, то вектор-функции
и
являются решениями систем
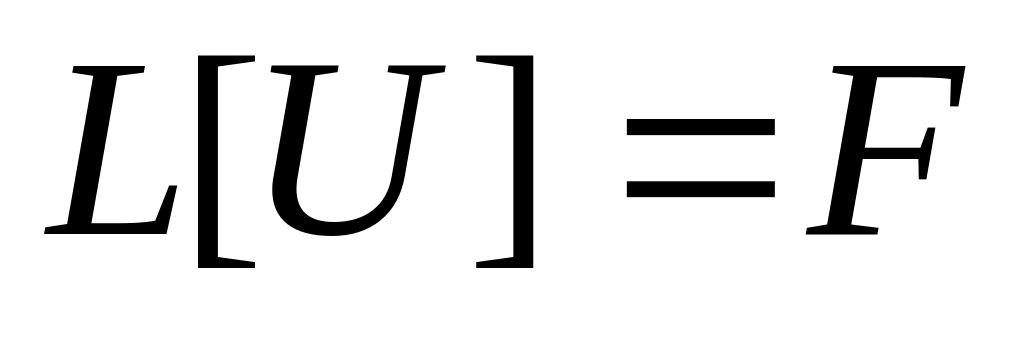и
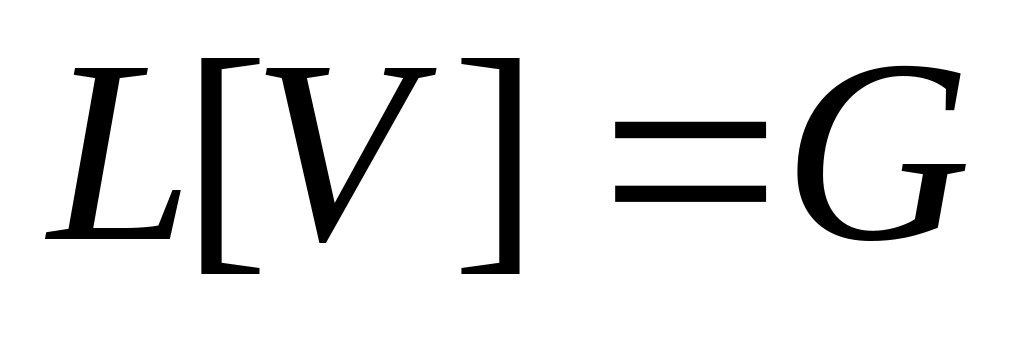соответственно.
Доказательство:
,
,
,
.
38. Лнсду. Метод Лагранжа вариации произвольных постоянных для отыскания частного решения. Теорема об интегрируемости.
- (1) ЛНСДУ
Пусть
- ФСР соответствующей однородной системы
ДУ. Запишем ее общее решение:
,
для отыскания частного решения, положим
произвольные константы функциями, т.е.
будем искать частное решение в виде
.
Подставим в систему (1):
.
Перегруппируем члены:
.
Для
получена линейная неоднородная
алгебраическая система с определителем,
равным вронскиану, т.е. не равным 0,
следовательно, существует единственное
решение.
Т. об интегрируемости: если в известна ФСР соответствующей однородной системы, то общее решение неоднородной всегда может быть найдено в квадратурах.
39. Лнсду с ПостК.
Т.: общее решение ЛНСДУ с постоянными коэффициентами всегда может быть найдено в квадратурах.
Доказательство:
,
решение соответствующей однородной
системы может быть найдено по методу
Эйлера, частное решение неоднородного
может быть найдено методом Лагранжа.
Т.: общее решение ЛНСДУ с постоянными
коэффициентами и СПЧ в виде квазиполиномов
(1) может быть получено в элементарных
функциях.
Замечания:
1) числа
и
для всех
должны быть одни и те же. В противном
случае используется принцип суперпозиции.
,
где
,
,
если
- корень
кратности
,
,
если
- не корень
,
и
- многочлены степени
с неопределенными коэффициентами;
2) если в (1) все многочлены
или
,
то удобнее использовать метод комплексных
амплитуд.
а) если
,
то перейдем к вспомогательной системе
.
Тогда
подбираем в виде
,
а
б) если
,
, то перейдем к вспомогательной системе
.
Тогда
подбираем в виде
,
а
40. Динамическая интерпретация нормальной соду. Фазовое пространство. Фазовая траектория.
Системы обыкновенных ДУ часто описывают динамику какого-либо процесса или физического явления.
,
(1) – динамическая система.
Обычно предполагается, что для (1)
выполняются условия т. Коши-Пикара.
Переменные
,
описывающие состояние системы – фазовые.
Пространство фазовых переменных –
фазовое пространство. В любой момент
времени состояние динамической системы
изображается точкой в фазовом пространстве
– это фазовая или изображающая точка.
Траектория движения фазовой точки –
фазовая траектория. Фазовая траектория
– проекция интегральной кривой на
фазовое пространство вдоль оси времени
.
На фазовой траектории стрелкой указывается
направление, отвечающее движению фазовой
точки со временем. Скорость движения
фазовой точки по фазовой траектории –
фазовая скорость.