Несобственные интегралы второго рода (несобственные интегралы от разрывных функций) (25).

Пусть функция f(x) определена и непрерывна при и терпит разрыв в точке x=c, тогда принимают как определенного интеграла при , т. е. предел называют несобственным интегралом второго рода. Сходящийся если этот предел существует и расходящимся если этот предел не существует.

Аналогично вводится понятие несобственные интегралы второго рода с точкой разрыва подынтегральной функции.

Пусть функция f(x) непрерывна при и терпит разрыв в точке c, тогда и этот предел существует, то интеграл второго рода от функции f(x) называется сходящийся, если этот предел не существует то расходящийся.

Пусть функция f(x) интегрирована на [a,b] всюду, кроме точки (функция a<c<b). В этом случае несобственные интегралы второго рода и если каждый из этих пределов существует и конечен то называют сходящимся, если же хотя бы один из этих пределов не существует то – расходящимся.

Главное значение несобственных интегралов второго рода: Если при пределы существуют, то вводят понятие главное значение и если этот предел существует то он называется главным значением несобственного интеграла второго рода. Если же этот предел не существует то главное значение расходится.

Для несобственного интеграла второго рода справедливы свойства (1) – (3) как и для несобственных интегралов первого рода.

Свойства несобственных интегралов 1го рода.

4. Если для любого , а сходится, то сходится и несобственный интеграл и при этом справедливо неравенство т. е. неравенство для функции можно интегрировать в смысле несобственного интеграла первого рода.

5. Если для любого а интеграл расходится, то расходится и интеграл от . Замечание: Свойства (1) и (2) позволяют делать оценки на несобственные интегралы первого рода, либо сверху либо снизу (первое свойство – сверху, второе свойство – снизу).

6. Если сходится то сходится и интеграл и при этом называется абсолютно сходящимся. Замечание: , Если же интеграл расходится, а интеграл сходится то он называется условно сходящимся. Замечание: Из выше приведенных утверждений следует что из расходимости не следует расходимость : он может быть как сходящимся, так и расходящимся. Свойства (1), (2) и (3) формулируются аналогично и для других несобственных интегралов первого рода с другими приделами.

Комплексные числа (26).

Натуральные числа N: 0,1,2,3,… Целые числа: 0,

Рациональные числа: 1/2,1/3, 3/5 Иррациональные числа: и т. д.

Все это действительные числа. Обобщением действительных чисел являются комплексные числа z=x+iy где x-действительная часть комплексного числа R_eZ,

y- мнимая часть комплексного числа I_mZ, i- мнимая единица i²=-1

Z=x+iy=R_eZ+iI_mZ ( ), Z=x+iy называется алгебраической формой записи числа. Если I_mZ=0, то Z=x – действительное число. Если R_eZ=0, то Z=iy – число мнимое комплексные число. Если R_eZ= I_mZ=0, то Z=0

Два комплексных числа Z₁=x₁+iy₁, и Z₂=x₂+iy₂ называются равными если R_eZ₁=R_eZ₂ (x₁=x₂) и I_mZ₁= I_mZ₂ (y₁=y₂). Комплексное число Z=x+iy и называются комплексно сопряженными.

Геометрический смысл комплексных чисел:

Р ассмотрим Z=x+iy. Каждому Z ставится в соответствии точка M(x,y) на комплексной плоскости Z и наоборот.

Ось OX (абсцисс) называется действительной осью, а ось OY (ординат) называется мнимой осью.

Р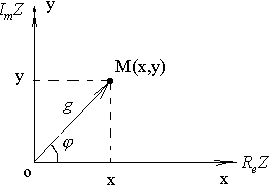 ассмотрим вектор: Любому вектору и преобразуем. Возьмем полярную систему координат точка M(x,y) , g – называется модулем комплексного числа, а - аргументом числа Z ( ). и определены неоднозначно а с точностью до числа кратного . Используя формулу (1) получим тригонометрическую форму записи комплексного числа . Используя формулу Эллера получим: , - действительные числа. Рассмотрим частные случаи:

Если - действительные числа. Если , , . В общем случаи: Модуль комплексного числа , argZ находится из уравнения

П ример:

R_eZ=1

I_mZ=-1

Замечание: Комплексно сопряженные числа Z=x+iy и геометрически изображаются двумя точками на комплексной плоскости зеркально симметричны относительно действительной оси (R_eZ). В показательной форме , то .

Действия над комплексными числами (27).

1. Сложение: Суммой двух комплексных чисел Z₁=x₁+iy₁ и Z₂=x₂+iy₂ называется Z=Z₁+Z₂=(x₁+x₂)+i(y₁+y₂). 2. Вычитание: Разностью двух комплексных чисел Z₁=x₁+iy₁ и Z₂=x₂+iy₂ называется Z которое будучи сложенным с Z₂ дает Z₁ Z=Z₁+Z₂=>Z₁=Z₂+Z=(x₁-_{_}x₂)+i(y1-y2), при сложении и вычитании комплексных чисел они должны быть представлены в алгебраической форме.

3. Умножение

Пр-ем комплексных чисел z1 b z2 называется такое комплексное число

Пр-р:

Если к.ч. , то

4. Деление.

такое к.ч. , что

определения деления сводится к определении умножения.

Пример:

5. Возведение к.ч. в целую степень.

(IV)

6. Возведение к.ч. в дробную степень извлечения корня.

Имеются n различных к.4. Zк, кат. имеют 1 и тот же модуль , а их аргументы

Все эти к.ч. лежат на окружности радиусом в вершинах правильного n-угольника, вписанного в эту окружность(n>=3). При n=2- на концах диаметра этой окружности.