Интегрирование по частям в определенном интеграле (15).

Докажем формулу:

, где и непрерывные функции на

Доказательство: так как и непрерывны, то

или , но

Отсюда следует

Приближённые методы вычисления неопределённых интегралов. Формулы прямоугольников. Формула трапеций (16)

1. Формулы прямоугольников. Пусть требуется вычислить приближённо: разобьем отрезок [a,b] на n равных частей точками x₀=a, x₁…x_n=b

1.) Первая формула прямоугольника вычисляет интеграл с недостатком.

2.) Вторая формула

прямоугольника вычисляет интеграл с избытком.

Объединяя формулы 1. и 2. Получим:

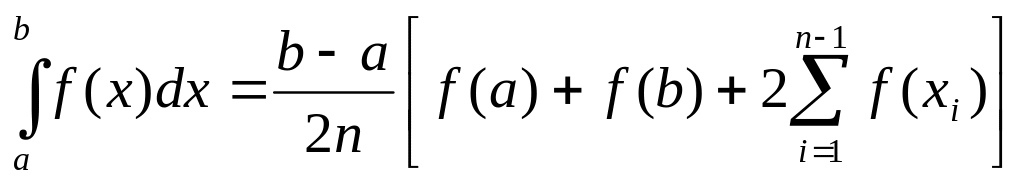
2. Формула трапеций.

Разобьем отрезок [a,b] на n равных частей точками x₀=a, x₁…x_n=b Шаг:

Заменим дуги каждой из криволинейных трапеций их хордами

формула трапеции.

Приближённые методы вычисления неопределённых интегралов. Формула параболы (формула Симпсона) (17)

3. Формула параболы (формула Симпсона). Разобьем отрезок [a,b] точками a=x₀, x₁, x₂…x_2n=b на 2n равные части с шагом . Заменим дуги каждой из кривых трапеций между точками (x_0,x₁,x₂), (x_2,x₃,x₄) параболами y=Ax²+Bx+C

сумме площадей криволинейных трапеций ограниченных параболами. Найдём площадь каждой из криволинейных трапеций ограниченных параболами. Для этого введём специальную систему координат так, что бы:

Из условий f(x_i)=y(0); f(x_i-1)=y(-h); f(x_i+1)=y(h);

где i=1,2,3…(2n-1);

- формула параболы (Симпсона)

Применение определенного интеграла к вычислению площадей плоских областей в декартовых координатах и областей заданных параметрически (18).

1. Вычисление площадей плоских областей:

а). Площадь плоской области в прямоугольники декартовой системы координат: Пусть область S задана уравнениями ; ; ; ; ;

Если f(x) отрицательна :

Если же S ограничена сверху графиком функции , снизу , слева x=a, справа x=b и для всех

Тогда и следовательно

Замечание:

б) площадь плоской области, заданной параметрически.

Пусть область задана параметрически:

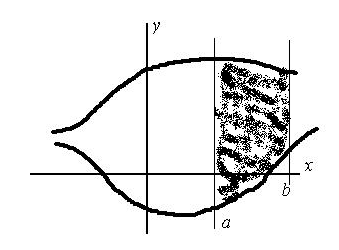
Примечание: если область задана параметрически ; . Тогда

Применение определенного интеграла к вычислению площадей плоских областей заданных в полярной системе координат (19).

Пусть область задана уравнением , , т.е. найдем площадь криволинейного сектора. Для этого разобьем область лучами на частей с шагом

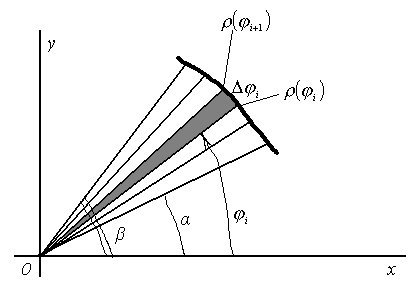
Т.к. мало, то Следовательно этот элемент - равнобедренный треугольник с точностью до бесконечно малого. Его площадь (по первому замечательному пределу). Итак или в дифференциальной форме . Следовательно

Примечание: если область задана уравнениями

тогда площадь области равна

Применение определенного интеграла к вычислению объемов тел вращения (20).

а) Пусть область задана уравнениями:

Область вращается вокруг . Найдем этого тела вращения.

Разобьем тело вращения плоскостями перпендикулярными плоскости . Обозначим:

-объем элементарного тела, на которое разделилось тело вращения. Т.к. мало, то

Следовательно

Б) Пусть кривая x=g(y) непрерывна на отрезке [c,d] вращается вокруг оси Оу тогда:

V_{y =} dy=g(y) Vy_i=

В) Кривая y=f(x) определённая и непрерывная на [a,b] вращается вокруг оси OY

Разобьем это тело на элементарные области. Объём тела

Г) Кривая x=g(y) определённая и непрерывная на [c,d] вращается вокруг оси Ox