Интегрирование рациональных функций (5-6).

1. Интегрирование неправильной рациональной дроби сводится к интегрированию многочлена и правильной рациональной дроби.

2. Интегрирование правильной рациональной дроби сводится к интегрированию простейших дробей вида I-IV.

Интегрирование правильной рациональной дроби:

Зная вычисляем К₂, зная К₂ вычисляем К₃ и т. д. При разложении правильной рациональной дроби на сумму простейших дробей вида I-IV с неопределенными коэффициентами необходимо определить эти коэффициенты для этого используем метод неопределенных коэффициентов.

Для того чтобы найти коэффициенты А₁, А₂, … , М_αs, N_αs и т.д. приведем правую часть к наименьшему общему знаменателю т. е. к Q(x), после этого приравняем коэффициенты стоящие при одинаковых степенях в левой и правой частях этих дробей в результате получаем систему линейных уравнений относительно этих коэффициентов решая которые находят эти коэффициенты. Замечание: Часть коэффициентов в разложении правильной рациональной дроби на простые могут быть найдены более простым методом, методом вычеркивания, а именно коэффициенты при старших степенях x(x-a_i) т. е. А_α1,.., В_α2

Интегрирование некоторых тригонометрических

функций (подстановки ; ) (7).

Рассмотрим интегралы от выражения -рациональная дробь от двух переменных , т.е. отношение двух многочленов двух переменных, например;

используют другие подстановки, которые также рационализируют исходный интеграл. Рассмотрим некоторые из этих подстановок. Для этого нам потребуются следующие свойства рациональных функций:

1)

2)

2.Если то рационализируется подстановкой

Действительно,

т.е. рационализируется.

3.Если , то рационализируется подстановкой

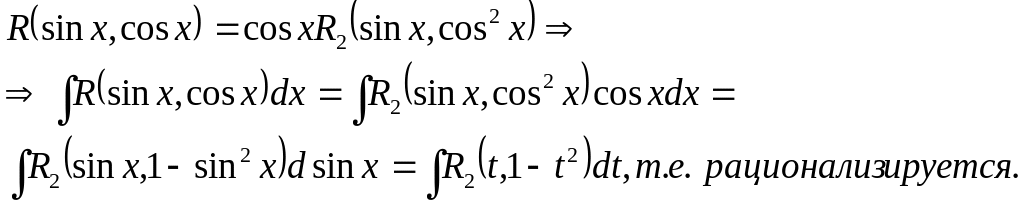
4.Если , то рационализируется подстановкой

т.е. рационализируется.

5.Интегралы вида

Интегрируется применением тригонометрических функций

Интегрирование некоторых тригонометрических

функций (подстановка ) (8).

Рассмотрим интегралы от выражения -рациональная дробь от двух переменных , т.е. отношение двух многочленов двух переменных, например;

1. рационализируется, т.е. сводятся к интегралу от рациональной дроби относительно новой переменной и называется универсальной тригонометрической подстановкой. Эта подстановка довольно громоздкая.

Действительно,

Воспользуемся формулами:

Тогда т.к. рациональная дробь от рациональной дроби есть рациональная дробь, то -рационализируется. -рациональная дробь.

Интегрирование некоторых иррациональных функций интегралы от линейных иррациональностей, интегралы от дробно линейных иррациональностей (9).

1. Интегралы от линейных иррациональностей.

Рассмотрим интегралы вида:

называются интегралы от линейных иррациональностей, где R-рациональные дроби от своих аргументов, -несократимые арифметические дроби.

Такие интегралы рационализируются подстановкой , где

, где - целые числа

, т.е. рационализируется.

- рациональная дробь.

Интегралы от дробно линейных иррациональностей:

Интегралы вида: называются интегралами от дробно линейных иррациональностей, они рационализируются подстановкой .

целые числа, R- рациональная дробь по t.