Линейное дифференциальное уравнение первого порядка. Уравнение Бернулли (32).
Д.у.
вида
,
где
-постоянные
или непрерывные функции ~x
называются линейными д.у. первого
порядка. Неоднородным, если
и однородным, если
.
Его решение ищут в виде
Так
как у нас имеется лишняя степень свободы,
то на одну из функции наложим дополнительное
условие, в нашем случае потребуем, чтобы
,
тогда для функции
получим уравнение
Итак,
Замечание:
линейное
д.у. первого порядка, когда
,
т.е. д.у. вида
может быть решено и другим способом,
как линейное д.у. первого порядка с
постоянными коэффициентами.
К
линейным д.у. первого порядка примыкает
и уравнение Бернулли, т.е. уравнение
вида:
Это уравнение можно привести к линейному
д.у. подстановкой
Замечание:
1)
К уравнению Бернулли приводит задача
о движении тела в среде, когда сила
сопротивления среды зависит от скорости
нелинейно, т.е.
2)
Решая уравнение Бернулли ищут , не
приводя его к линейному подстановкой
,
т.е. как линейное.
Уравнения в полных дифференциалах. Интегрирующий множитель (33).
Д.у.
первого порядка вида
называется дифференциальным уравнением
в полных дифференциалах, если
Это
отношение является необходимым и
достаточным условием, чтобы д.у.
было д.у. в полных дифференциалах, т.е.
-
общий интеграл.
Действительно:
1)
Необходимость: докажем, что если
,
то
,
так как
,
то
и
Отсюда находим
и
Но
,
если они непрерывны в данной точке
2) Достаточность: Пусть
Докажем,
что существует
такая,
что
Отсюда следует
и
. Проинтегрируем любое из этих уравнении
по x
или по y
соответственно, например первое.
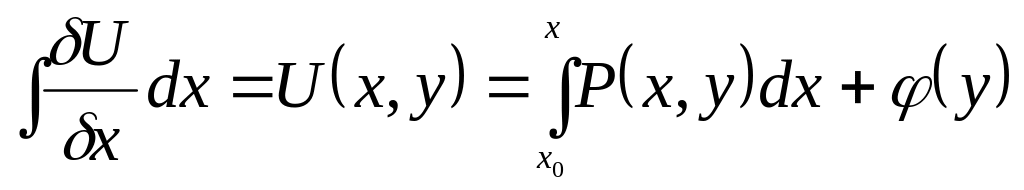
Итак
Отсюда находим
Отсюда
Из
(*) и (**) следует
Общий
интеграл исходного д.у. есть
и следовательно
Замечание:
из
доказательства пункта 2 следует метод
решения уравнений в полных дифференциалах,
т.е. из условий
ищется
Если
д.у.
не является д.у. в полных дифференциалах,
т.е.
,
то существует такой множитель
,
который называется интегрируемым
множителем, что д.у.
будет д.у в полных дифференциалах, т.е.
(3)
Это уравнение является д.у. частных
производных для нахождения функции
.
В двух частных случаях уравнение легко
решится:
1)
Из уравнения (3) находим
(4)
Если
это так, то
находится из (4):
2)
Из уравнения (3) находим
(5)
Если
это так, то
находится из (5):
Замечание: д.у. в полных дифференциалах может быть как д.у. с разделяющимися переменными, однородным или линейным. Следовательно, перед тем как проверять условие необходимо убедиться, что оно не является д.у. с разделяющимися переменными, однородным, линейным или уравнением Бернулли. (смотрите последний пример)
д.у.
с разд. переменными и однородным.
-
однородное.
Вынужденные колебания.
где p>0,
q>0.
Рассмотрим частный случай, когда внешняя
сила
1)
p0
и
.
Общее решение однородного уравнения
имеет вид:
где
.
Частное решение неоднородного
дифференциального уравнения будем
искать в виде:
т.к.
находим
и
.
Подставляем
в неоднородное дифференциальное
уравнение
;
;
;
;
;
;
;
где
;
;
;
;
;
;
где
тогда общее решение неоднородного
дифференциального уравнения примет
вид:
где
.
При
т.е. по истечении достаточно большого
промежутка времени, система ведёт себя
по закону вынуждающей силы. Колебания
происходят с частотой вынуждающей
силы.
;
;
Имеет
место минимум при:
;
где
и
;
;
при этой частоте в системе возникает
резонанс, т.е.
будет максимальна.
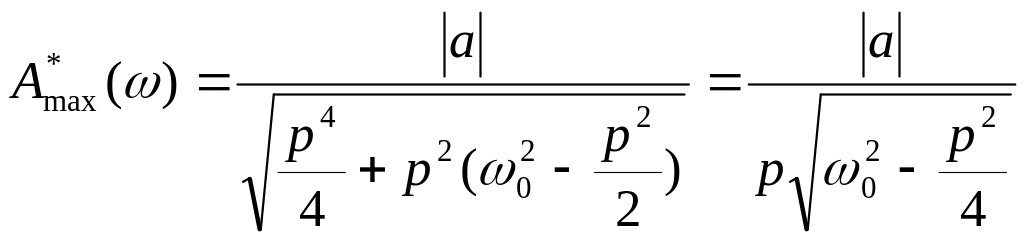при p=0
и =0,
А*
это явление называется резонансом.
2)
Пусть p=0,
,
,
а)
т.е.
;
;
;
;
Находим:
Отсюда находим:
откуда M=0
т.к.
,
а
;
;
;
y
– есть сумма двух гармонических
колебаний с частотой 0
и
б)
;
где
;
;
При
=0
отсюда N=0,
;
;
при t
и y
т.е. резонанс при =0
и p=0