Первообразная. Неопределённый интеграл и его свойства (1).

Опр. Первообразной для функции на интервале называют функцию , дифференцируемую на и удовлетворяющую условию . Отсюда следует, что функция , также является первообразной для функции на , т.к.

Опр. Совокупность первообразных для данной функции на называют неопределенный интеграл и обозначают .

называется подынтегральным выражением, -подынтегральной функцией. По определению . Нахождение первообразной для данной функции на называется интегрированием функции .

Свойства:

1. 

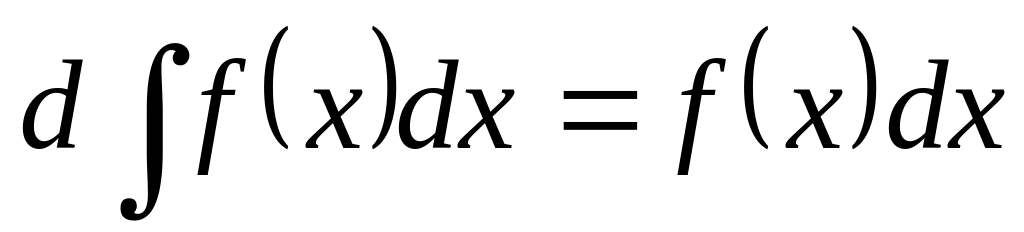
2. Так как имеет ,т.е. то

3.

4.

5.

Таблица неопределенных интегралов

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

17. 

18. 

19. 

Замена переменной в неопределенном интеграле (2).

1. Внесение под знак дифференциала

2. Замена переменной

Сделаем подстановку . Причем она определена на , так, что существует обратная функция , определенная на и будем считать, что существует производная на . Тогда Если имеет первообразную , то , таким образом после замены переменной в неопределенном интеграле и нахождение у первообразной необходимо возвратиться к старой переменной.

Доказательства: Продифференцируем соотношение по x, используя свойство (1) получим:

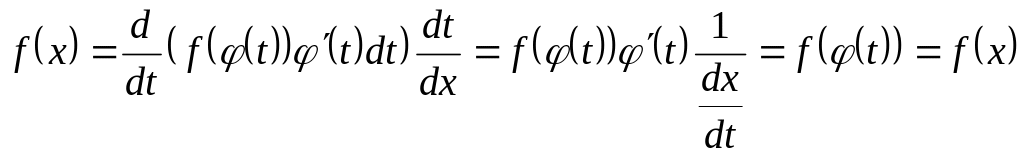, что и требовалось доказать.

Пример:

, т.е. на практике чаще приходится делать обратную подстановку

Интегрирование по частям в неопределенном интеграле (3)

Пусть функции определены и дифференцируемы на и пусть подынтегральное выражение может быть представлено в виде:

, тогда

Доказательство: продифференцируем

и проинтегрируем по х.

или

. Отсюда

Существует несколько классов функций, которые могут быть проинтегрированы этим методом:

1. Интегралы, содержащие одну из функций lnx, arcsinx и т. д. Такие интегралы берутся методом интегрирования по частям, причем через U обозначается одна из этих функций(аdV, то что осталось).

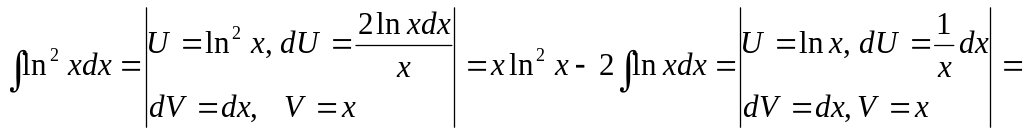
2. Интегралы вида ; ;

интегрируются по частям при этом каждый раз в качестве U принимается многочлен.

3. Интегралы вида: , , ,

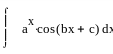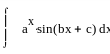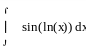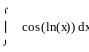
двукратное применение формулы интегрирование по частям в следствии получаем линейное уравнение относительно исходного интеграла а решая которое и находим искомый интеграл.

Прим.: №1

№2

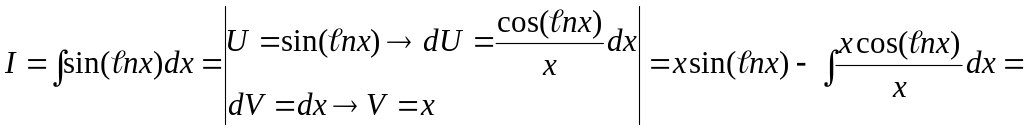
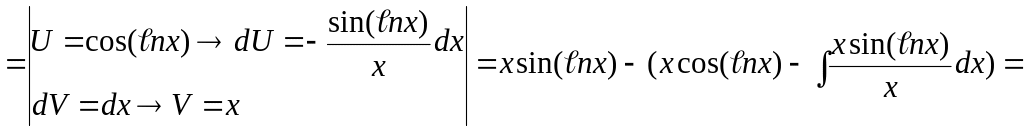
4. Существуют и другие типы неопределенных интегралов, которые могут быть вычислены применением формулы интегрирования по частям.

Пример:

Разложение рациональной дроби на простейшие (4).

Отношение 2х мн-нов и наз. рац. дробью.

– рац. дробь.

m – порядок мн-на

n – порядок мн-на

Если , то рац. дробь наз. неправильной рац. др.

– непр. рац. дробь.

– пр. рац. дробь.

Если же m < n, то рац. дробь – пр. рац. дробь.

Любую правильную рациональную дробь можно разложить на сумму простейших дробей вида:

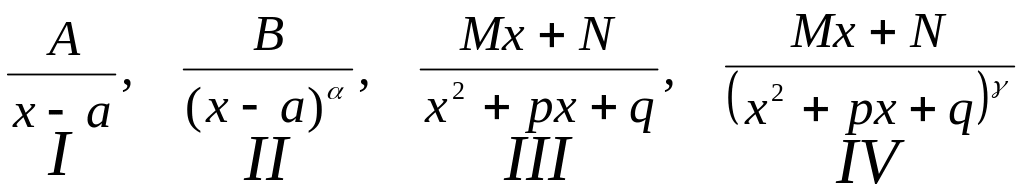. Правильные рациональные

дроби вида I-IV называется простейшими рациональными дробями.

Теорема № 1: Если многочлен Q(x) имеет корень а кратности , т. е. Q(x)=(x-a) , где Q₁(a) 0, то правильная рациональная дробь можно представить в виде причем последняя дробь правильная. Доказательство: Запишем тождество определим const А таким образом чтобы многочлен делился на нацело т. е. А было корнем этого многочлена. (по теореме Безу) т. к. Q₁(a) 0 и P(a) 0 то А определим однозначно следовательно подстановка выражения P(x)-AQ₁(x)=(x-a)+P₁(x) в тождество дает: Следствие № 1: К правильной рациональной дроби можно применить последовательно теорему № 1:

Следствие № 2: Если Q₁(x) имеет действительные корни, то к правильной рациональной дроби можно применить теорему № 1 и следствие № 1, т. е. если в правильной рациональной дроби многочлен имеет разложение , где не имеет действительных корней. - действительные числа, то разложим на сумму дробей I,II и правильную рациональную дробь . Аналогично теорема имеет место и в том случае когда многочлен имеет комплексно сопряженные корни , т. е. раскладываются на квадратные трехчлены , где .

Теорема № 2: Если многочлен Q(x) имеет комплексно сопряженные корни a+bi кратности , т. е. имеют разложения вида Q(x)=(x²+px+q)Q₁(x), где (не имеет действительных корней), а Q₁(x) не делится на цело на x²+px+q, то правильная рациональная дробь можно представить в виде причем последняя дробь правильная. Доказательство: Как и при доказательстве теоремы № 1 стартуем с тождества 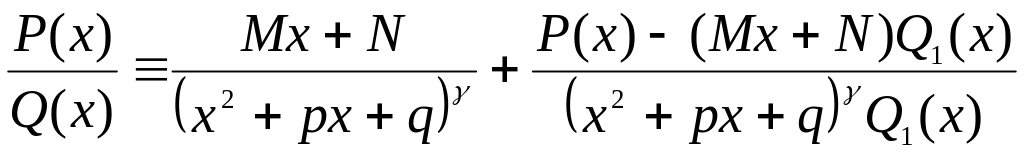коэффициенты M и N определены однозначно если потребовать чтобы многочлен P(x)-(Mx+N)Q₁(x) делился на x²+px+q нацело т. е. по теореме Безу P(x)-(Mx+N)Q₁(x)=( x²+px+q)P₁(x) и P₁(x) на x²+px+q нацело не делится. Подставляя это выражение в тождество получаем 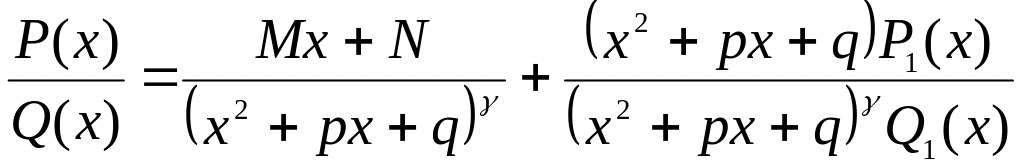. Следствие № 3: К правильные рациональные дроби можно применить теорему № 2 в результате правильная рациональная дробь разложена на сумму дробей вида III, IV и правильная рациональная дробь со знаменателем Q₁(x), , если многочлен Q₁(x) делится на Q₂(x), то к правильной рациональной дроби можно применить теорему № 2 и ее следствие № 3 т. о. Если многочлен Q(x) имеет разложение , то правильную рациональную дробь можно разложить используя теоремы № 1 и № 2 и их следствия на сумму простейших дробей вида I-IV.

(5).