13)Классы симметрии, общие определения и системы обозначения.
Полное сочетание элементов симметрии кристаллического многогранника называется его классом симметрии или точечной группой симметрии.
Перечень всех элементов симметрии кристалла, записанный в виде их символов, называется формулой симметрии или видом симметрии.
На первом месте принято писать оси симметрии от высших к низшим, на втором – плоскости симметрии, затем центр.
Таким образом, полный набор всех элементов симметрии для гексаэдра запишется следующим образом: 3L44L36L29PC.
В Международном символе каждого класса пишутся только основные, или так называемые порождающие элементы симметрии, а порожденные элементы симметрии, которые можно вывести из сочетаний порождающих элементов, не пишутся.
В качестве порождающих элементов предпочтение отдается плоскостям.
В качестве символов, записываемых в международные обозначения, используются символы, обозначающие как отдельные элементы симметрии, так и их сочетания, а именно:
n – ось симметрии (n = 1, 2, 3, 4, 6);
–
инверсионная ось
симметрии ( n
= 3, 4, 6);
m – плоскость симметрии;
nm – ось симметрии порядка n и плоскость симметрии m, направленная вдоль оси (продольная плоскость симметрии);
n/m – ось симметрии порядка n и плоскость симметрии m, направленная перпендикулярно оси (поперечная плоскость симметрии);
n2 – ось симметрии порядка n и n осей 2-го порядка, ей перпендикулярных;
(n/m)m = n/mm – ось симметрии порядка n и плоскости симметрии m, параллельные и перпендикулярные ей.
Классы
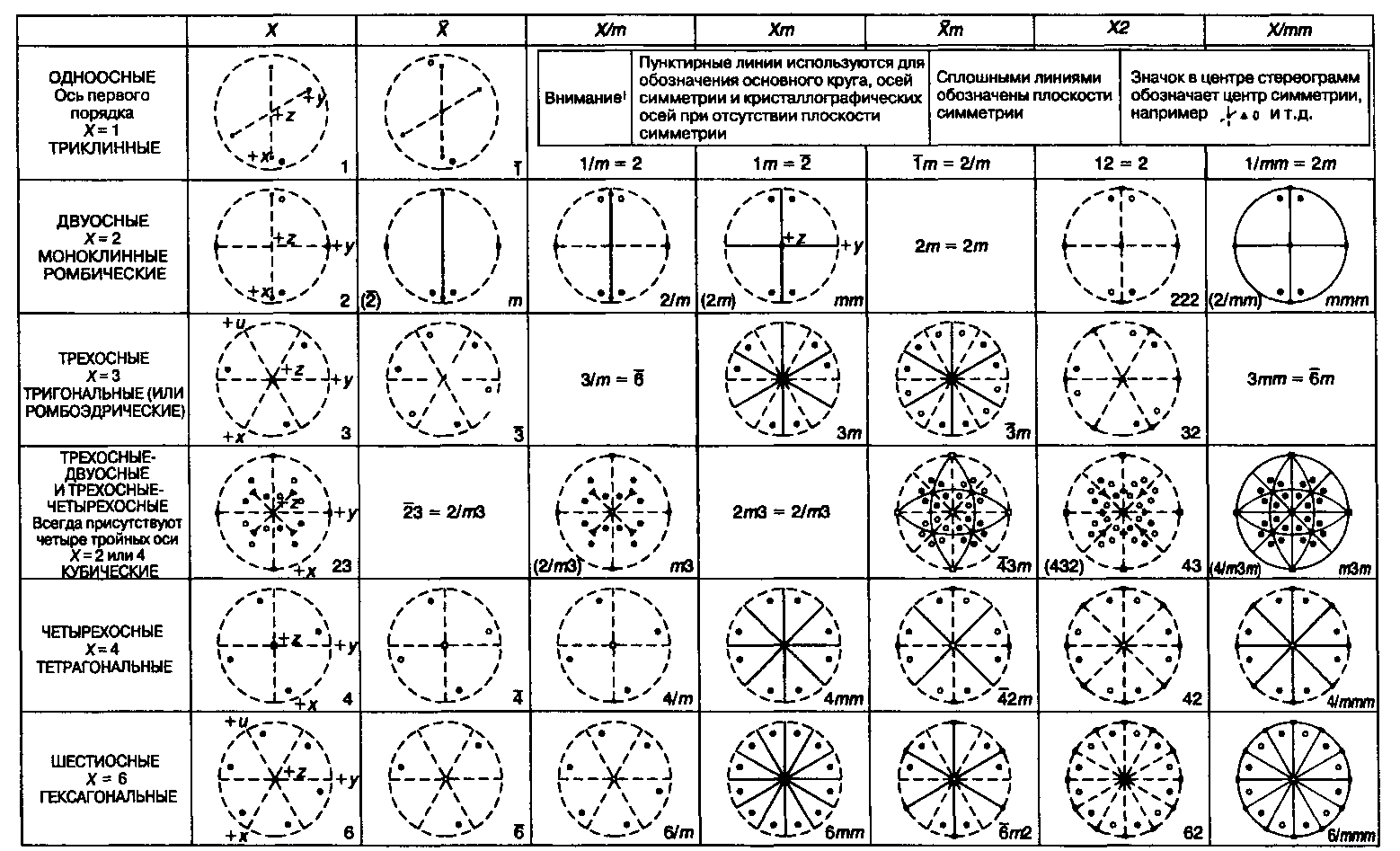
На рис. 3.37 показано, как путем операции симметрии при последовательном добавлении новых элементов выводятся 32 возможных класса внешней симметрии кристаллов.
Эта процедура включает построение стереограммы и нанесение на нее полюса грани, находящегося в общей позиции (см. разд. 3.6.1). Затем на стереограмму накладываются элементы симметрии и записываются образуемые простые формы. При этом одни элементы симметрии порождают другие. По международной системе обозначений (Германа—Могена), указанных в правом нижнем углу каждой клетки на рис. 3.37, для определения какого-либо класса требуется только минимум элементов симметрии, хотя при этом предполагается наличие и других ее элементов. На рис. 3.37 помимо символов, написанных в низу каждой клетки, для каждого класса на стереограм-ме общей простой формы обозначен полный набор элементов симметрии. Оси симметрии обозначены простыми символами: двойные — овалами, тройные — треугольниками, четверные — квадратами и шестерные — шестиугольниками. Эти символы для поворотных осей закрашены черным цветом, а для инверсионных оставлены незакрашенными. Сплошными линиями на стерео-граммах нанесены плоскости симметрии; основной круг и оси, не совпадающие с зеркальными плоскостями, обозначают пунктиром.
В международной системе обозначений поворотная ось показана цифрой, соответствующей степени повторения: 1, 2, 3, 4 или б, а инверсионная ось — цифрой с черточкой над ней: 2 и т.д, плоскость симметрии (зеркальная) обозначается буквой т. На рис. 3.37 в заголовках колонок использованы следующие обозначения:
X — одна поворотная ось
X — одна инверсионная ось
Х/т —поворотная ось с плоскостью симметрии, перпендикулярной к ней Хт —поворотная ось с плоскостью симметрии, не перпендикулярной к ней (обыч-* но наличие вертикальной плоскости сим
метрии)
Хт — инверсионная ось с плоскостью симметрии, не перпендикулярной к ней Х2 — поворотная ось с двойной осью симметрии, перпендикулярной к ней Х/гпт —поворотная ось с одной плоскостью симметрии, перпендикулярной к ней, и с другой — не перпендикулярной.
При написании символа основная ось симметрии ставится первой. (На рис. 3.37 эта ось помещена под прямым углом к плоскости страницы, за исключением моноклинных классов 2, т и 2/т, у которых она расположена слева направо, так что +z остается в центре.) Затем следует символ плоскости симметрии, перпендикулярной к этой оси, если такая плоскость присутствует, после чего указываются второстепенные оси.
Следует учитывать определенные дополнительные правила. В кубической системе к таковым относится то, что в символе первое место занимают оси и плоскости симметрии, связанные с осями х, у и z. Второе место отводится четырем тройным осям, которые всегда присутствуют в кубической точечной группе. Поэтому вторым символом у нее всегда является 3. Третье место в этой точечной группе принадлежит элементам симметрии, связанным с гранями диагональных направлений.
Определенные тонкости существуют также в порядке написания символов для классов Зm, 42m и 6m2. Если бы мы написали 32m, то следовало бы полагать, что зеркальная плоскость не перпендикулярна к оси симметрии, что неверно. Некоторые авторы применяют символ 32/m, но международная система обозначений совершенно не использует оси симметрии, которые возникают автоматически в любом случае. Порядок расположения обозначений в двух других указанных символах подразумевает взаимоотношения горизонтальных элементов с выбранными кристаллографическими осями, что представляет интерес своей связью с внутренним пространственным расположением атомов.
