1. Статистическая обработка данных и прогнозирование

Функции, реализующие статистические методы обработки и анализа данных, в Excel реализованы в виде специального программного расширения - надстройки Пакет анализа, которая входит в поставку данного программного продукта и может устанавливаться (или не устанавливаться) по желанию пользователя. Установка надстройки Пакет анализа производится точно так же, как и установки прочих надстроек, то есть через меню Сервис > Надстройки, после чего в диалоговом окне Надстройки необходимо пометить пункт Пакет анализа и нажать кнопку ОК (рис. 6.16).

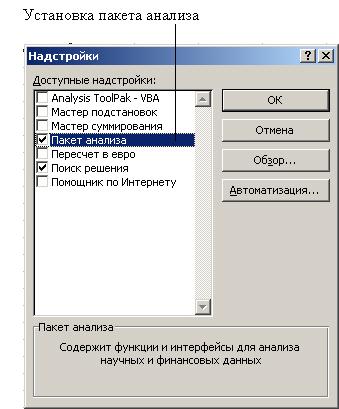
Рис. Установка пакета анализа

Если процесс установки Завершается успешно, то в меню Сервис появляется еще один пункт - Анализ данных (рис. 6.17), а также при создании формул становится доступной новая группа функций - статистические.

Рис. Окно Анализ данных, вызываемое из меню Сервис > Анализ данных

Проблема изучения взаимосвязей различного рода показателей является одной из важнейших в экономическом анализе. В конечном счете, основное содержание любой экономической политики может быть сведено к регулированию экономических переменных, осуществляемому на базе выявленной тем или иным образом информации об их взаимовлиянии. Целью статистического исследования является обнаружение и исследование соотношений между статистическими (экономическими) данными и их использование для изучения, прогнозирования и принятия решений. Любые экономические данные представляют собой количественные характеристики каких-либо экономических объектов. Они формируются под действием множества факторов, не все из которых доступны внешнему контролю. Неконтролируемые факторы могут принимать случайные значения из некоторого множества значений и тем самым обусловливать случайность данных, которые они определяют. Стохастическая природа экономических данных обусловливает необходимость применения специальных статистических методов для их анализа и обработки. Поэтому фундаментальными понятием статистического анализа являются понятия вероятности и случайной величины. Конечно, Excel не предназначен для комплексного статистического анализа и обработки данных (в отличие от специального статистического программного обеспечения, такого как STATISTICA, Eviews, TSP, SPSS, Microfit и др.). Однако и на базе электронных таблиц можно провести некоторую статистическую обработку данных. В частности, в рамках Excel с помощью команд, доступных из окна Анализ данных (рис. 6.17), можно провести: - описательный статистический анализ (Описательная статистика); - ранжирование данных (Ранг и персентиль); - графический анализ данных (Гистограмма); - прогнозирование данных (Скользящее среднее, Экспоненциальное сглаживание); - регрессионный анализ (Регрессия) и др. Термин "регрессия" широко применяется в научной литературе для обозначения так называемой статистической зависимости между двумя (несколькими) сериями значений каких-либо величин. Определение "статистическая" предполагает, что рассматриваемая зависимость реализуется как некоторая общая тенденция, от которой возможны случайные отклонения в ту или иную сторону. Практические методы определения параметров регрессии (или, как еще говорят, регрессионного анализа) базируются на достаточно сложном математическом аппарате, составляющем предмет таких дисциплин, как математическая статистика, многомерный статистический анализ и др. В табл. 6.2 приведены статистические функции, позволяющие пользователю реализовывать операции регрессионного анализа (выявления зависимостей между рядами данных) непосредственно на рабочем листе электронной таблицы.

Таблица Статистические функции для регрессионного анализа

Функция	Назначение функции и ее аргументы	Тип
ЛИНЕЙН	Определяет параметры линейного тренда для заданного массива ЛИНЕЙН(знач.У; знач. X; констанста; стат.)	Встроенная
ТЕНДЕНЦИЯ	Определяет предсказанные значения в соответствии с линейным трендом для заданного массива (метод наименьших квадратов) ТЕНДЕНЦИЯ(знач.У; знач. X; новые знач.Х; константа;)	Встроенная
ПРЕДСКАЗ	Определяет предсказанное значение функции в заданной точке на основе линейной регрессии ПРЕДСКАЗ(Х; знач.У; знач. X)	Встроенная
НАКЛОН	Определяет коэффициент для независимой переменной в уравнении парной регрессии НАКЛОН(знач.У; знач. X)	Встроенная
ОТРЕЗОК	Определяет отрезок, отсекаемый на оси ординат линией линейной регрессии ОТРЕЗОК(знач.У; знач. X)	Встроенная
КВПИРСОН	Определяет квадрат коэффициента корреляции Пирсона КВПИРСОН(знач.У; знач. X)	Встроенная
ПИРСОН	Определяет коэффициент корреляции Пирсона (степень линейной зависимости между двумя множествами данных) ПИРСОН(массив 1 ; массив 2)	Встроенная
СТОШУХ	Определяет стандартную ошибку предсказанных значений У для каждого X СТОШУХ(знач.У; знач. X)	Встроенная
РОСТ	Аппроксимирует данные экспоненциальной кривой  РОСТ(знач.У; знач. X; новые знач.Х; константа;)	Встроенная

Перечисленные функции имеют очень широкий спектр экономических приложений. Например, в качестве иллюстрации техники использования статистических функций Excel рассмотрим задачу построения парной линейной регрессии между доходностью отдельно взятой акции и доходностью рыночного портфеля. Сформулированная проблема основывается на подходе к описанию поведения финансового рынка с помощью так называемой модели САРМ. Не вдаваясь в подробности ее описания, заметим, что одним из базовых ее допущений является предпосылка о возможности описания связи между доходностью акции и доходностью рыночного портфеля с помощью уравнения.

CapitalAssetPricingModel (Модель оценки финансовых активов) (CAPM) - экономическая модель для оценки акций, ценных бумаг, деривативов и/или активов путем соотношения риска и ожидаемого дохода. CAPM основывается на той идее, что инвесторы требуют дополнительный ожидаемый доход (рисковую премию), если их просят взять на себя дополнительный риск.

2. Корреляционный анализ занимается степенью связи между двумя переменными, x и y. 

Сначала предполагаем, что как x, так и y количественные, например рост и масса тела. Предположим, пара величин (x, у) измерена у каждого из n объектов в выборке. 

Мы можем отметить точку, соответствующую паре величин каждого объекта, на двумерном графике рассеяния точек. 

Обычно на графике переменную x располагают на горизонтальной оси, а у — на вертикальной. Размещая точки для всех n объектов, получают график рассеяния точек, который говорит о соотношении между этими двумя переменными.

Коэффициент корреляции Пирсона

Соотношение х и у линейное, если прямая линия, проведенная через центральную часть скопления точек, дает наиболее подходящую аппроксимацию наблюдаемого соотношения. 

Можно измерить, как близко находятся наблюдения к прямой линии, которая лучше всего описывает их линейное соотношение путем вычисления коэффициента корреляции Пирсона, обычно называемого просто коэффициентом корреляции. 

Его истинная величина в популяции (генеральный коэффициент корреляции) (греческая буква «ро») оценивается в выборке как r (выборочный коэффициент корреляции), которую обычно получают в результатах компьютерного расчета. 

Пусть (x₁. y₁), (x₂, y₂),…,(x_n, y_n) - выборка из n наблюдений пары переменных (X, Y).

Выборочный коэффициент корреляции r определяется как 

,  

где ,- выборочные средние, определяющиеся следующим образом:

В данном узле рассчитывается корреляционная матрица. Корреляционный анализ применяется для оценки зависимости выходных полей данных от входных факторов и устранения незначащих факторов.

Принцип корреляционного анализа состоит в поиске таких значений, которые в наименьшей степени коррелированны (взаимосвязаны) с выходным результатом. Такие факторы могут быть исключены из результирующего набора данных практически без потери полезной информации. Критерием принятия решения об исключении является порог значимости. Если корреляция (степень взаимозависимости) между входным и выходным факторами меньше порога значимости, то соответствующий фактор отбрасывается как незначащий.

При выборе метода расчета Максимум взаимокорреляционной функции будет вычислен максимум из коэффициентов корреляции двух процессов, рассчитанных при всевозможных временных сдвигах. Следует применять, если необходимо узнать линейную зависимость между двумя процессами или частями процессов происходящих с определённым временным лагом. Расчет коэффициента корреляции Пирсона происходит с использованием алгоритма БПФ. Здесь можно выделить два шага: быстрое преобразование Фурье и Расчет коэффициента корреляции.

3. Факторный анализ - это методика комплексного и системного изучения и измерения воздействия факторов на величину результативного показателя. Факторы в результате анализа получают количественную и качественную оценку. Каждый показатель может в свою очередь выступать и в роли факторного, и результативного.

Различают следующие противоположные типы факторного анализа:

• детерминированный и стохастический;

• прямой и обратный;

• одноступенчатый и многоступенчатый;

• статический и динамический;

• ретроспективный (исторический) и перспективный (прогнозный).

Факторный анализ может быть одноуровневым и многоуровневым.

Одноуровневый факторный анализ - используется для исследования факторов только одного уровня (одной ступени) подчинения без их детализации на составные части. Например, y = ax+b.

Многоуровневый, многоступенчатый факторный анализ - проводит детализацию факторов а и b на составные элементы с целью изучения их сущности. Детализация факторов может быть продолжена. В таком случае изучается влияние факторов различных уровней соподчиненности.

Статический факторный анализ - применяется при изучении влияния факторов на результативные показатели на соответствующую дату.

Динамический факторный анализ - представляет собой методику исследования причинно-следственных связей в динамике.

Ретроспективный факторный анализ - изучает причины изменения результатов хозяйственной деятельности за прошлые периоды.

Перспективный факторный анализ - исследует поведение факторов и результативных показателей в перспективе.

Основные задачи факторного анализа:

1. Выявление, поиск факторов.

2. Отбор факторов для анализа исследуемых показателей.

3. Классификация и систематизация их с целью обеспечения системного подхода.

4. Моделирование взаимосвязей между результативными и факторными показателями.

5. Расчет влияния факторов и оценка роли каждого из них в изменении величины результативного показателя.

6. Работа с факторной моделью (практическое ее использование для управления экономическими процессами).

Факторный анализ - это один из способов снижения размерности, то есть выделения во всей совокупности признаков тех, которые действительно влияют на изменение зависимой переменной. Или группировки сходно влияющих на изменение зависимой переменной признаков. Или группировки просто сходно изменяющихся признаков. Предполагается, что наблюдаемые переменные являются лишь линейной комбинацией неких ненаблюдаемых факторов. Некоторые из этих факторов являются общими для нескольких переменных, некоторые характерно проявляют себя только в одной. Те, что проявляют себя только в одной, очевидно, ортогональны друг другу и не вносят вклад к ковариацию переменных, а общие - как раз и вносят эту ковариацию. Задачей факторного анализа является как раз восстановление исходной факторной структуры исходя из наблюдаемой структуры ковариации переменных, несмотря на случайные ошибки ковариации, неизбежно возникающие в процессе снятия наблюдения.

Коэффициент взаимосвязи между некоторой переменной и общим фактором, выражающий меру влияния фактора на признак, называется факторной нагрузкой(Factorload) данной переменной по данному общему фактору. Значение (мера проявления) фактора у отдельного объекта называется факторным весом объекта по данному фактору.