Подготовка к факторному анализу

При подготовке к факторному анализу часто (некоторые методы этого не требуют, но большая часть - требует) составляют ковариационные и корреляционные матрицы. Это матрицы, составленные из ковариации и корреляций векторов-атрибутов (строки и столбцы - атрибуты, пересечение - ковариация/корреляция).

Ковариация двух векторов:

математическое ожидание 

Корреляция двух векторов:

,

- дисперсия.

Обратите внимание, что в этом случае корреляция и ковариация двух векторов - числа, так как считаются через матожидание вектора, а матожидание вектора - число.

Таким образом, мы переходим от матрицы, составленной из объектов (которые могут быть и не математическими), к матрице, оперирующей уже исключительно математическими понятиями, и абстрагируемся от объектов, уделяя внимания только атрибутам.

Нахождение первичной структуры факторов Метод главных компонент

Метод главных компонент стремится выделить оси, вдоль которых количество информации максимально, и перейти к ним от исходной системы координат. При этом некоторое количество информации может теряться, но зато сокращается размерность.

Этот метод проходит практически через весь факторный анализ, и может меняться путем подачи на вход разных матриц, но суть его остается неизменной.

Основной математический метод получения главных осей - нахождение собственных чисел и собственных векторов ковариационной матрицы таких, что:

RV = λV, где

λ - собственное число R, R - матрица ковариации, V - собственный вектор R. Тогда :

RV − λV = 0

V(R − λE) = 0

и решение есть когда:

| R − λE | = 0,

где R - матрица ковариации, λ - собственное число R, E - единичная матрица. Затем считаем этот определитель для матрицы соответствующей размерности.

V находим, подставляя собственные числа по очереди в

V(R − λE) = 0

и решая соответствующие системы уравнений.

Сумма собственных чисел равна числу переменных, произведение - детерминанту корелляционной матрицы. Собственное число представляет собой дисперсию оси, наибольшее - первой и далее по убыванию до наименьшего - количество информации вдоль последней оси. Доля дисперсии, приходящаяся на данную компоненту, считается отсюда легко: надо разделить собственное число на число переменных m.

Коэффициенты нагрузок для главных компонент получаются делением коэффициентов собственных векторов на квадратный корень соответствующих собственных чисел.

Алгоритм nipals вычисления главных компонент

На практике чаще всего для определения главных компонент используют итерационные методы, к примеру, NIPALS:

0. Задается 0 < ε₁< 1 - критерий окончания поиска главного компонента, и 0 < ε₂< 1 - критерий окончания поиска главных компонентов, исходная отцентрированная матрицаX, i=1 - номер главной компоненты.

1. Берется - вектор-столбец, k - шаг алгоритма, j - любой столбец (просто чтобы было с чего начинать апроксимизацию).

2. Вектор T_kтранспонируется.

3. Считается .

4. P_kнормируется

5. Считается новый 

6. Если тоиP_k- вектора весов и нагрузок соответственно для i-ой главной компоненты. Если нет, тои иди на 2.

7. .

8. Если | X| < ε, то стоп - найдены все основные компоненты, нас удовлетворяющие. Иначе i++. Иди на 1.

4. Использование методов идентификации

Идентификацией называется нахождение оптимальной в некотором смысле модели, построенной по результатам наблюдений над входными и выходными переменными объекта. Задачи идентификации Задачей идентификации называется обратная задача системного синтеза.

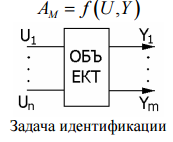
AM = f (U Y, ) Задача идентификации Среди задач идентификации выделяют два типа: 1. Структурная идентификация (в широком смысле слова); 2. Параметрическая идентификация (идентификация в узком смысле слова).

Структурная идентификация

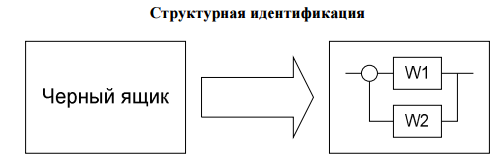Подразумевает построение модели типа «черный ящик», т.е. об объекте мы ничего не знаем. Главная задача: определение структуры модели. Рекомендации по решению задач структурной идентификации: 1. Определить тип (класс) моделей. а) Начинать построение модели с физической модели (по известным законам физики, не забывая о цели построения модели); б) Начинать с самых простых моделей (линейная, непрерывная, одномерная и т.д.); в) Постараться преобразовать модель к виду линейной регрессии:

Определение размера или порядка модели (определение количества внутренних переменных модели). Определение ковариационных (зависимость от шумовых характеристик) и корреляционных (взаимосвязь между определенными двумя внутренними переменными) матриц. На сегодняшний момент существует несколько методов исследования ковариационных и корреляционных матриц, которые позволяют определить недостаточность или избыточность модели. 3. Параметрическая идентификация (способ параметризации модели)

Методы в алгоритме идентификации: Текущие данные, Выбор класса модели, Выбор критерия согласия.

5. Использование методов прогнозирования

Метод прогнозирования- это способ исследования объекта прогнозирования, направленный на разработку прогнозов.

Методика прогнозирования- это совокупность специальных приемов и правил разработки конкретных прогнозов.

Прием прогнозирования- это математическая или логическая операция, направленная на получение конкретных результатов в процессе разработки прогнозов.

Классификация методов прогнозирования осуществляется по трем основным признакам: 1) по степени формализации методов; 2) по общему принципу действия; 3) по способу получения прогнозной информации.

По степени формализации методы прогнозирования делятся на формализованные и интуитивные.

Формализованные методы используются в том случае, когда информация об объекте прогнозирования носит в основном количественный характер, а влияние различных факторов можно описать с помощью математических формул.

Интуитивные методы применяются тогда, когда информация количественного характера об объекте прогнозирования отсутствует или носит в основном качественный характер и влияние факторов невозможно описать математически.

В свою очередь эти две группы можно разделить по общему принципу деятельности и способу получения прогнозной информации. Формализованные методы подразделяются на методы экстраполяции и методы моделирования.

К методам экстраполяции относятся метод скользящей средней, метод экспоненциального сглаживания, метод наименьших квадратов, а к методам моделирования – методы информационного моделирования (патентный и публикационный), статистического моделирования, логического моделирования (прогнозной аналогии, «дерево целей»).

Интуитивные методы прогнозирования делятся на индивидуальные и коллективные экспертные оценки. Причем индивидуальные экспертные оценки основаны на обобщении мнений отдельных экспертов, выраженных независимо друг от друга. К ним относятся: метод интервью, метод анкетного опроса, аналитический метод, метод написания сценария. Коллективные экспертные оценки базируются на получении объединенной оценки от всей группы специалистов-экспертов, выработанной при непосредственном контакте. К таким методам относятся метод Дельфи, метод «мозговой атаки», метод экспертных комиссий.

В экономическом прогнозировании применяются два принципиально отличающихся друг от друга подхода – поисковый и нормативный.

Поисковый прогнозможно определить как условное продолжение в будущее наблюдаемых тенденций исследуемого явления или процесса, закономерности развития которых в прошлом и настоящем достаточно хорошо известны. Причем, если возможные организационные решения способны существенно видоизменить наметившиеся тенденции, от них следует абстрагироваться. Основная цель поискового прогноза состоит в том, чтобы выяснить, что может произойти, какие проблемы могут возникнуть при сохранении существующих тенденций развития.

Нормативный прогнозоснован на экстраполяции от будущего к настоящему, т.е. на определении оптимального состояния изучаемого объекта на период прогнозирования с использованием средств целеполагания по заранее сформулированным критериям. При нормативном прогнозе сначала задается некоторая цель развития объекта прогнозирования, а затем определяется траектория движения прогнозируемого процесса или явления. Цель данного подхода – выявление альтернативных путей достижения оптимума.

Поисковый и нормативный прогнозы не взаимоисключают, а дополняют друг друга. Как правило, поисковый прогноз составляет первый этап разработки прогнозного исследования, на котором получается сравнительная оценка возможных вариантов развития. На втором этапе осуществляется разработка нормативного прогноза, который исходит из познанных общественных закономерностей, тенденций, потребностей развития, а также формулировка программы возможных путей, мер и условий для достижения поставленных целей с привлечением необходимых ресурсов и средств.