10)Сложные элементы симметрии.

сложные элементы симметрии – зеркально-поворотные и инверсионные оси.

Инверсионная ось симметрии n-го порядка (Li) это прямая линия при повороте вокруг которой на некоторый угол с последующим отражением в центральной точке фигуры как в центре инверсии фигура совмещается сама с собой. Совмещают в себе поворотную ось и действие центра симметрии.

Зеркально-поворотные оси я-го порядка сочетают, как на это указывает их название, поворот на 360 / и с отражением в плоскости, перпендикулярной к оси.

11)Теоремы о сочетании операций симметрии.

Сочетания элементов симметрии и их взаимные расположения подчиняются всем положениям математической теории абстрактных групп.

Два последовательно выполненных симметричных преобразования всегда могут быть заменены эквивалентным третьим преобразованием.

Теорема 1. Линия пересечения двух плоскостей симметрии является осью симметрии, причем угол поворота вокруг этой оси вдвое больше угла между плоскостями.

Теорема 1а (обратная). Поворот вокруг оси симметрии на угол α эквивалентен отражениям в двух плоскостях симметрии, проходящих вдоль оси; угол между плоскостями равен α/2, причем отсчет угла производится в направлении поворота.

Теорема 2. Точка пересечения четной оси симметрии с перпендикулярной ей плоскостью симметрии есть центр симметрии.

В международных символах такое сочетание

обозначается n/m, где n порядок оси.

Теорема 2а (обратная). Если есть четная ось симметрии и на ней центр симметрии, то перпендикулярно этой оси проходит плоскость симметрии.

Теорема 2 б (обратная). Если есть центр симметрии и через него проходит плоскость симметрии, то перпендикулярно этой плоскости через центр проходит четная ось симметрии.

Теорема 3. Если есть ось симметрии порядка n и перпендикулярно этой оси проходит ось 2, то всего имеется n осей 2-го порядка, перпендикулярных оси n-го порядка.

Обозначение такого сочетания n2.

Теорема 4. Если есть ось симметрии n-порядка и вдоль нее проходит плоскость симметрии, то таких плоскостей имеется n. Обозначения nm.

Теорема 5 (теорем Эйлера). Равнодействующей двух пересекающихся осей симметрии является третья ось, проходящая через точку их пересечения.

Теорема 6. Плоскость, проходящая вдоль четной инверсионной оси симметрии, приводит к появлению оси 2-го порядка, перпендикулярной инверсионной оси и проходящей по биссектрисе угла между плоскостями.

Полное сочетание элементов симметрии записывается как

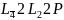международный символ .

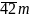12)Кристаллографические категории, сингонии.

В зависимости от числа особых направлений кристаллы делятся на три категории: низшую, среднюю, высшую.

К низшей категории относятся кристаллы, которые имеют несколько особых направлений. В таких кристаллах нет осей симметрии порядка выше 2-го.

К средней категории относятся кристаллы, имеющие одно особое направление, которое совпадает с простой или инверсионной осью симметрии 3-го, 4-го или 6-го порядков. Вдоль особого направления могут быть расположены продольные плоскости симметрии; перпендикулярно особому направлению могут находиться поперечная плоскость симметрии, а также оси симметрии 2-го порядка.

К высшей категории относятся кристаллы, не имеющие особых направлений. Кроме осей симметрии 2-го порядка в этих кристаллах обязательно имеется четыре оси симметрии

3-го порядка, и могут быть также три простых или инверсионных оси симметрии 4-го порядка.

Кристаллы делят на семь сингоний. В одну сингонию относят кристаллы, имеющие одинаковую симметрию элементарной ячейки и одинаковую систему координат.

В общем система координатных осей будет косоугольной с различными масштабными отрезками по осям координат. К низшей категории относятся три сингонии: триклинная, моноклинная и ромбическая.

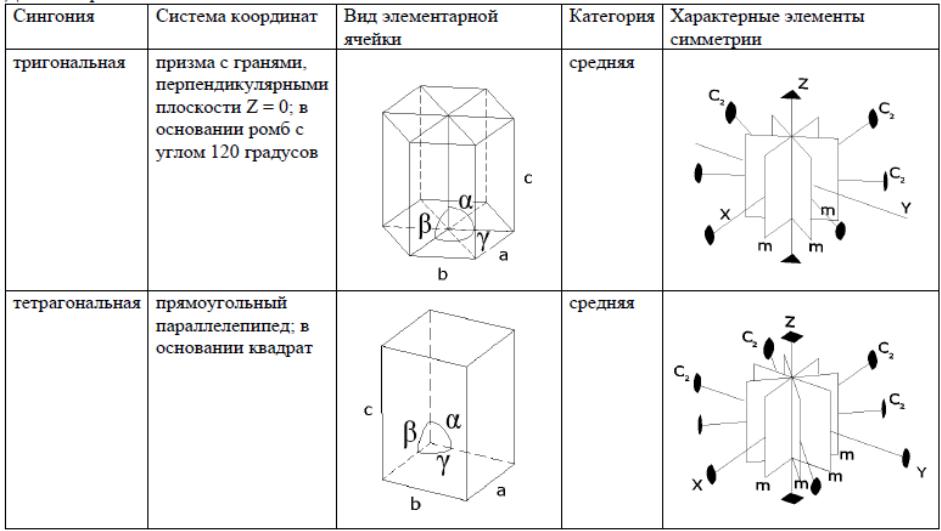
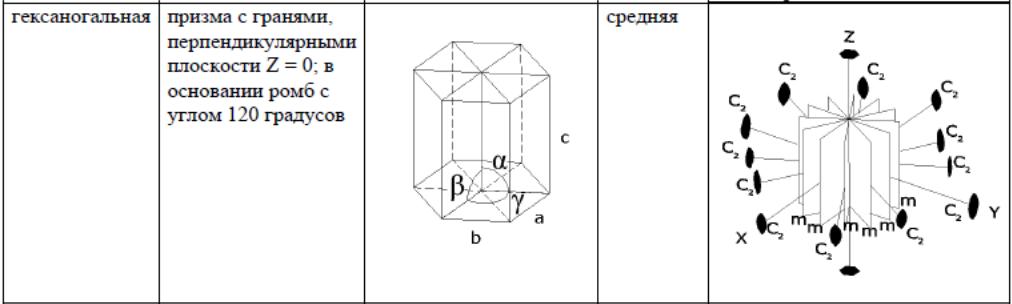
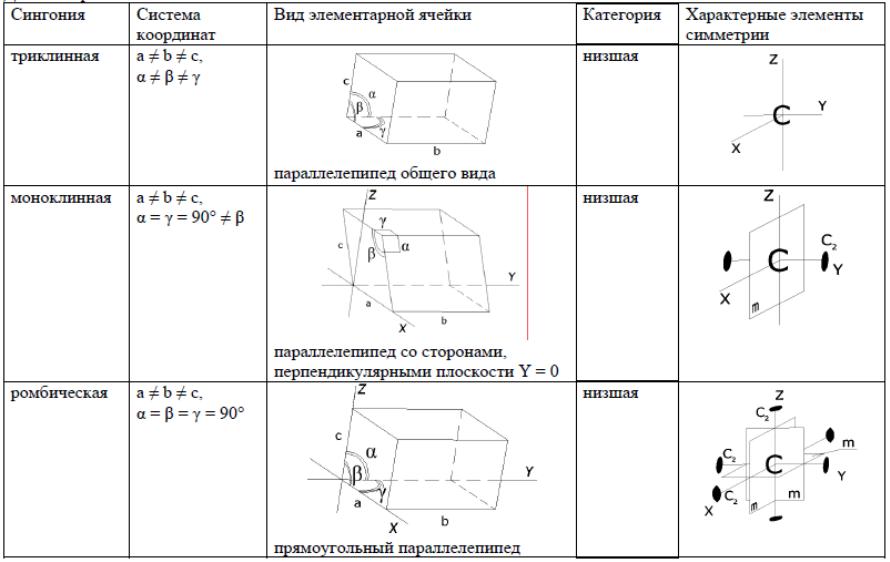Средняя категория: тригональная, тетрагональная и гексагональная сингонии

Кубическая сингония является единственной сингонией высшей категории. Элементарная ячейка здесь представляет собой куб. Характерными элементами симметрии являются четыре оси симметрии 3-го порядка, направленные вдоль объемных диагоналей куба.