14. Задача Кеплера

Рассмотрим важный случай центрального поля, когда потен­циальная энергия равна (4.21) Силу, действующую на материальную точку, найдем по формуле (4,22), где — единичный вектор, направленный по радиусу. Знак плюс относится к полю отталкивания, когда сила направлена от центра. Знак минус - полю при­тяжения. Для рассматриваемого потенциального поля сила обрат­но пропорциональна квадрату радиуса. Такую зависимость силы от расстояния имеют поле тяготения сферически симметричной массы и электрическое поле точечн. или сферически симметрич­н. заряда.

Ур-ие траектории получим, вычисляя интеграл (4.18). За­пишем его для поля притяжения, выбирая знак минус в (4.21). Положим также постоянную =0 и выберем знак плюс перед интегралом. Такой выбор постоянной и знака перед инте­гралом соответствует выбору оси ОХ в направлении на положение минимального удаления материальной точки от центра. Тогда ин­теграл имеет вид

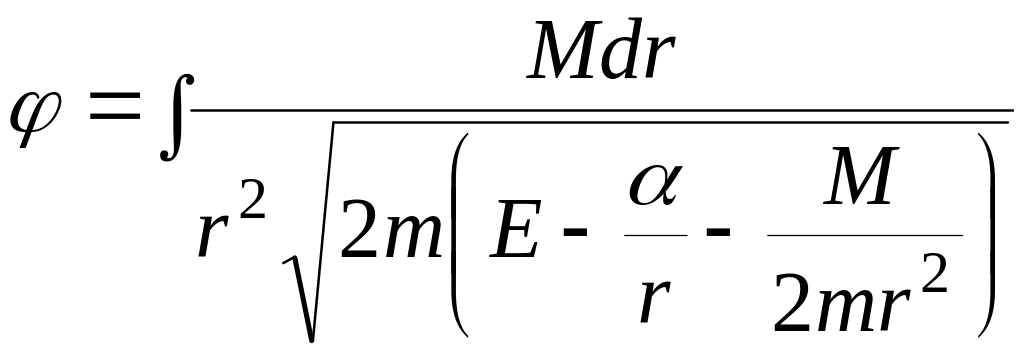(4.23) Интеграл (4.23) приводится к табличному интегралу путем заме­ны и выделением полного квадрата под знаком корня. Результат интегрирования можно записать в форме (4.24)

где введены две новые постоянные: параметр и эксцентриситет . Они равны:

; (4.25) Уравнение (4.24) задает в полярных координатах одно из кони­ческих сечений: гиперболу, параболу или эллипс. Начало поляр­ной системы координат совпадает с одним из фокусов гиперболы или эллипса или с фокусом параболы. Вид конического сечения зависит от величины эксцентриситета . При уравнение зада­ет гиперболу. В этом случае положительна энергия материальной точки: (4.26)

Материальная точка, движущаяся по гиперболе, может уйти на бесконечность и будет иметь там ненулевую скорость. При второе слагаемое в (4.26) обращается в 0 и энергия материаль­ной точки равна ее кинетической энергии . Если , то эксцентриситет и уравнение (4.24) задает пара­болу. Материальная точка по-прежнему может уйти на бесконеч­ность, но скорость ее на бесконечности =0. И наконец, при отрицательной энергии материальной точки ее эксцентри­ситет . Тогда уравнение (4.24) описывает эллипс. Движение материальной точки ограничено областью вблизи центра поля.

Е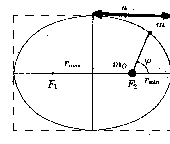 сли пренебречь взаимодействием планет между собой, то по­лученные для поля притяжения с результаты можно применить к описанию движения планет Солнечной системы. Так как масса Солнца >> массы планет Солнечной системы, то центр поля можно считать совпадающим с центром Солнца, а приведенную массу считать = массе планеты. Из з-на всемирного тяготения имеем . Выразим измеряе­мые астрономами величины ^— большую полуось орбиты и период обращения планеты — через энергию и момент импульса планеты. Из рис. 4.5 траектории планеты видно, что

; (4.27)

Размер большой полуоси эллипса не зависит от момента импульса материальной точки и определяется только ее энергией. Период обращения материальной точки вокруг центра найдем путем инте­грирования соотношения (4.11) закона площадей. За период обра­щения вокруг центра площадь, заметаемая радиусом-вектором ма­териальной точки, равна площади эллипса. Используя значения для и из (4.27), формулу для площади эллипса и закон площадей (4.11), получим

(4.28) Подставляя в (4.28) значения и из формул (4.27), найдем период обращения: (4.29)

Для планет Солнечной системы отношение . Lля них период обращения зависит только от величины большой полуоси орбиты. Эти рез-ты для движения материальной точки по эллипсу в центральном поле в приложении к движению планет Солнечной системы открыты Кеплером. За­коны Кеплера

Закон 1. Планета движется по эллипсу, в одном из фокусов ко­торого находится Солнце.

Закон 2. Площади, заметаемые радиусом-вектором планеты за одинаковые промежутки времени, равны.

Закон 3. Квадраты периодов обращения планет относятся как кубы их больших полуосей. Уравнение траектории для поля оттал­кивания, когда . : (4.30) и даются формулой (4.25). Единственно возможной траекторией в этом случае является гипербола, для которой и .