3. Энергия, з-н изменения кинетической энергии с-мы материальных точек.

Закон 2 Ньютона. Изменение количества движения пропорционально при­ложенной движущей силе и происходит по направлению той пря­мой, по которой эта сила действует.

Второй закон Ньютона связывает ускорение тела с действую­щей на него силой:

(1.1)

Так как масса — величина постоянная, то уравнение (1.1) мож­но записать в форме (1.6)

Если уравнение второго закона Ньютона (11) умножить скалярно на и учесть, что , то можно получить соотношение

(1.9)

Величина

называется кинетической энергией матери­альной точки, а произведение — работой силы на перемеще­нии . Изменение кинетической энергии материальной точки рав­но работе действующей на нее силы. Если элементарная работа силы является дифференциалом некоторой функции

(1.10)

то эта функция называется потенциалъной энергией. В этом случае из уравнения (1.9) вытекает закон сохранения механической энергии, равной сумме потенциальной и кинетической энергии:

(1.11)

Силы, для которых выполняется условие (1,10), называются потенциальными силами. Проекции потенциальной силы на оси координат выражаются через частные производные от потенциальной энергии:

; ; ; (1.12)

Несколько тел, каждое из которых можно рассматривать как материальную точку, составляют систему материальных точек. Для каждой материальной точки можно записать уравнение вто­рого закона Ньютона

(1.13)

В уравнении (1.13) индексы дают номер материальной точки. Действующие на материальную точку силы разделены на внеш­ние и внутренние . Внешние силы — это силы, действующие со стороны тел, не входящих в систему материальных точек. Вну­тренние силы — это силы, действующие на материальную точку со стороны других тел, составляющих систему материальных точек. Здесь — сила, действующая на материальную точку, индекс которой , со стороны материальной точки с номером .

Из уравнений (1.13) вытекают несколько важных законов. Если просуммируем их по всем материальным точкам системы, то по­лучим

(1.14) ,

Записывая уравнения изменения кинетической энергии (1.9) для всех материальных точек системы и суммируя их по всем ма­териальным точкам, получим

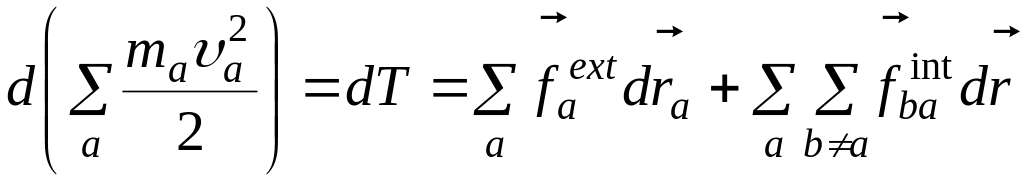(1.19)

где — кинетическая энергия системы материальных точек. В формуле (1.19) работа внутренних сил не обращается в пуль. Если сумма работ внешних и внутренних сил является полным дифференциалом, то из уравнения (1.19) вытекает закон сохранения полной механической энергии

(1.20)

Потенциальная энергия зависит от координат всех материальных точек. Силу, действующую на материальную точку с номером а, можно найти по формулам

(1.21)

где производные берутся по координатам материальной точки .

4. С-ма отсчета центра инерции. Преобразование импульса, момента импульса, энергии….

Пусть имеется система отсчета, которая движется поступатель­но со скоростью относительно неподвижной системы отсчета. Скорость может зависеть от времени. Механические величины в подвижной системе отсчета будем отмечать штрихами. Скорости материальной точки с номером в двух системах отсчета связаны соотношением (1.22) Подставляя (1.22) в формулу для импульса системы материальных точек ( ) получим: (1.23) Можно найти такую систему отсчета, в которой импульс системы материальных точек =0. Про такую систему отсчета естественно сказать, что это система отсчета, в которой система материальных точек как целое покоится. Это вовсе не означает, что скорости всех материальных точек равны нулю. Полагая в формуле (1.23) равным нулю, находим скорость такой системы отсчета: (1.24) Из соотношения (1.24) видно, что эта скорость может быть выра­жена как производная от следующего радиуса-вектора; . (1.25) Радиус-вектор указывает на точку, которая называется цен­тром инерции системы материальных точек. Из определения центра инерции видно, что он совпадает с центром масс системы материальных точек.

Всегда можно найти систему отсчета, в которой импульс системы материальных точек равен нулю. Эта система отсчета движется со скоростью центра инерции системы матери­альных точек и называется системой отсчета центра инерции. Из (1.23) видно, что импульс системы отсчета записывается через скорость центра инерции и массу системы материальных точек так же, как импульс одной материальной точки: , (1.26)

масса которой равна массе системы материальных точек и ско­рость которой равна скорости центра инерции. Закон изменения импульса системы материальных точек (1.16) тогда запишется как второй закона Ньютона для материальной точки:

(1.27) Центр инерции системы материальных точек движется как мате­риальная точка, масса которой равна массе системы материаль­ных точек и к которой приложена сила, равная сумме действую­щих на систему материальных точек внешних сил. В частности, если сумма внешних сил =0, то центр инерции движет­ся равномерно и прямолинейно, и система отсчета центра инерции является инерциальной системой отсчета.

Преобразование кинетической энергии при переходе в систему отсчета центра инерции. Подставляя закон сложения скоростей (1.22) в выражение для кинетической энергии системы, получим

Т.к. в системе отсчета центра инерции импульс системы мате­риальных точек =0, то последнее слагаемое пропадает и мы имеем (1.28)

К инетическая энергия системы материальных точек равна сумме кинетической энергии движения системы со скоростью центра инерции и кинетической энергии внутреннего движения материальных точек в системе отсчета центра инерции. Так как потенциальная энергия не зависит от системы отсчета, то аналогичное разбиение на внутреннюю энергию и энергию движения системы как целого будет справедливо для полной механической энергии: (1.29) В системе отсчета центра инерции момент импульса не зависит от выбора начала координат. Покажем это. Пусть начала коор­динат смещено из точки в точку , как показано на рис. 1.1. Тогда радиусы-векторы материальной точки относительно двух начал координат связаны равенством (1.30) Подставляя это выражение для в определение момента импульса системы материальных точек ( (1.18)), получим (1.31) Здесь — момент импульса системы материальных точек относительно нового начала координат. Так как в системе отсчета центра инерции импульс системы материальных точек равен нулю, то второе слагаемое в (1.31) обращается в нуль и. . Преобразование момента импульса системы материальных точек при переходе в систему отсчета центра инерции. Пусть в некоторый момент времени начала координат двух систем отсчета совпадают. Тогда . Скорости материальных точек относительно двух систем отсчета связаны соотношением (1.22). Подставляя (1.22) в определение момента импульса (1.18) и учи­тывая, что движущаяся система отсчета — это система отсчета инерции, получим . (1.32) Т.к. в системе отсчета центра инерции не зависит от выбора начала координат, то это равенство будет справедливо в любой другой момент времени, когда начала координат двух систем отсчета уже не будут совпадать. Второе слагаемое в (1.32) дает момент импульса системы материальных точек, движущихся как целое со скоростью центра инерции. Момент импульса с-мы мат. т. представляется в виде суммы собственного момента и момента импульса от движения системы материальных точек со скоростью центра инерции.