27. Производная по подвижному объему, ур-ние неразрывности. (Дифференциальные и интегральные соотношения, подвижный объем).

В механике сплошной среды многие величины задаются своими плотностями. Например, плотность массы, плотность импульса и плотность момента импульса определяются по формулам:

, , . (8.4)

Тогда те же величины для конечного объема сплошной среды по­лучаются интегрированием по объему: , , . (8.5)

Уравнения механики сплошной среды также могут быть записаны в дифференциальной и интегральной формах. Объем, по которому ведется интегрирование, может быть фиксированным или подвиж­ным. Под подвижным объемом в механике сплошной среды пони­мают объем, который движется вместе со сплошной средой. По­этому частицы сплошной среды не пересекают поверхность, огра­ничивающую подвижный объем.

Р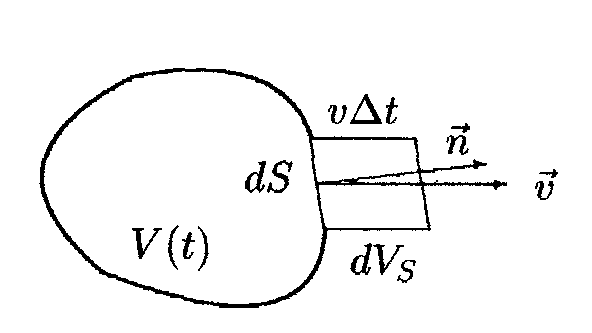 ис. 8.1 При вычислении производных по времени по подвижному объ­ему необходимо учитывать, что с течением времени подвижный объем может измениться. Как видно из рис. 8.1, за время площадка поверхности, ограничивающей объем, сместится на расстояние . За счет этого смещения объем увеличится на . Все изменение объема получается интегрировани­ем этого увеличения по замкнутой поверхности, ограничивающей подвижный объем:

. (8.6)

Если некоторая величина А задана объемной плотностью и вы­числена интегрированием по подвижному объему , то ее при­ращение за время складывается из двух частей: приращения, вызванного изменением плотности внутри объема, и приращения за счет изменения объема:

. (8.7)

Разделив соотношение (8.7) на и устремив к нулю, получим производную от величины А, вычисленной по подвижному объему:

. (8.8)

Поверхностный интеграл в формуле (8.8) с помощью теоремы Остроградского—Гаусса можно преобразовать в объемный:

. (8.9)

Подстановка этого объемного интеграла в равенство (8.8) приво­дит к следующим выражениям для производной по подвижному объему:

. (8.10)

Переход от одной формы к другой осуществляется при помощи соотношения

(8.2). Если положить , то величина А равна подвижному объему и формула (8.10) дает производную от подвижного объема, которая равна . (8.11)

Если , то величина подвижного объема остается постоянной при движении сплошной среды. Такая сплошная среда называется несжимаемой средой.

Положим в формуле (8.10) А = т. Так как частицы сплошной среды не пересекают границ подвижного объема, то т=const и производная от массы =0. Поэтому нулю должны быть равны подынтегральные выражения в (8.10), что даст уравнения , . (8.12)

Уравнения (8.12) называются уравнениями неразрывности и вы­ражают собой закон сохранения массы. Такие же уравнения вы­полняются для любой физической величины (например, заряда), которая остается постоянной внутри подвижного объема.

Найдем сейчас производную по времени от импульса сплошной среды, заключенной в подвижном объеме. Из определения им­пульса (8.5) и выражения (8.10) для производной имеем

. (8.13)

Сумма во внутренних скобках под знаком интеграла (8.13) обра­щается в нуль вследствие уравнения неразрывности (8.12). В ре­зультате получаем

. (8.14)

Аналогичным образом можно показать, что производная от мо­мента импульса конечного объема сплошной среды вычисляется по формуле

. (8.15)