22. Тензор инерции

Запишем момент импульса и кинетическую энергию твердого тела. Их можно представить в виде

, (6.11) . (6.12)

Здесь и — момент импульса и кинетическая энергия твердого тела в системе отсчета центра инерции твердого тела. В системе отсчета центра инерции твердое тело может только вра­щаться. Поэтому момент импульса и кинетическая энергия связа­ны только с вращением и должны выражаться через угловую ско­рость твердого тела. Начало подвижной системы координат поместим в центр инерции твердого тела и перейдем в систему отсчета центра инерции. Подставляя скорость в определение момента импульса и учи­тывая, что = 0, получим . (6.13)

Будем рассматривать только момент импульса и кинетическую энергию, обусловленные вращением тела, и отбросим индекс «вращ». Раскрывая в формуле (6.13) двойное векторное произведение, най­дем для момента импульса:

. (6.14)

Спроектируем равенство (6.14) на оси координат. Для проектиро­вания следует выбрать подвижные оси координат, которые жестко связаны с твердым телом. Проекция на ось ох имеет вид (6.15)

и может быть записана в форме (6.16)

с коэффициентами

,

,

.

Аналогичным образом получаются проекции на оси оу и ог. Все три проекции можно записать в виде . (6.18)

Здесь индексы i, j задают номер координатной оси. Величины являются компонентами симметричного тензора второго ранга, на­зываемого тензором инерции. Компоненты тензора инерции запи­сываются в виде следующей симметричной матрицы:

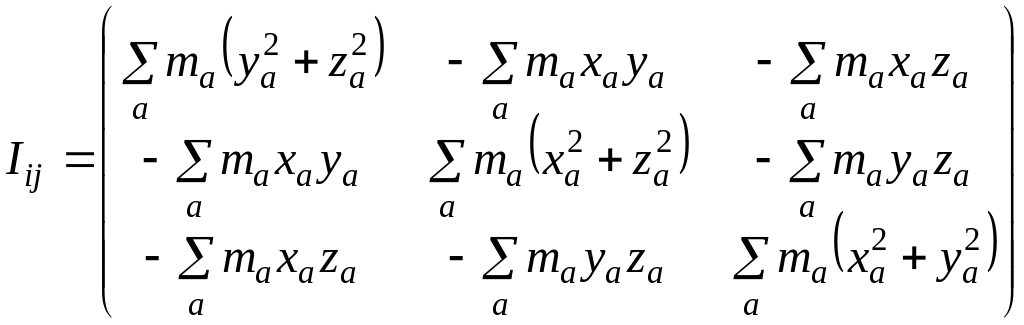(6.19)

Если твердое тело является сплошным, а не состоит из отдельных материальных точек, то суммы в (6.19) заменяются интегралами но объему твердого тела. Например, компонента - тензора инер­ции вычисляется по формуле

. (6.20)

Выразим теперь через тензор инерции кинетическую энергию вращения твердого тела. В системе отсчета центра инерции имеем

. (6.21)

Подставляя в формулу (6.21) выражения для проекций момента импульса из (6.18), получим для кинетической энергии твердого тела следующую формулу:

. (6.22)

Тензор инерции определяется распределением масс в твердом теле и является характеристикой твердого тела, не зависящей от характера движения твердого тела. Диагональные компоненты тензора инерции равны моментам инерции при вращении твердого тела вокруг осей, совпадающих с координатными осями подвижной системы координат. Недиагональные компоненты тензора инерции называются центробежными моментами инерции. Так как тен­зор инерции является симметричным тензором второго ранга, то преобразованием координат его можно привести к диагональной форме, когда недиагональные компоненты будут равны нулю. Оси декартовой системы координат, в которой тензор инерции имеет диагональную форму, называются главными осями инерции. Диа­гональные компоненты тензора инерции в главных осях инерции называются главными моментами инерции а обычно записыва­ются с одним индексом: I₁, I₂, I₃. В главных осях инерции момент импульса и кинетическая энергия твердого тела записываются в особенно простой форме:

, (6.23)

, , . (6.24)

Если твердое тело обладает некоторой симметрией, то напра­вления главных осей инерции совпадают с осями симметрии твер­дого тела. Поэтому при вычислении тензора инерции для таких твердых тел оси координат направляют по осям симметрии твер­дого тела.