Оценка точности вычисления определённого интеграла

Интеграл вычисляется по выбранной формуле (прямоугольников, трапеций, парабол Симпсона) при числе шагов, равном n, а затем при числе шагов, равном 2n. Погрешность вычисления значения интеграла при числе шагов, равном 2n, определяется по формуле Рунге: , для формул прямоугольников и трапеций  , а для формулы Симпсона  . Таким образом, интеграл вычисляется для последовательных значений числа шагов  , где n₀ — начальное число шагов. Процесс вычислений заканчивается, когда для очередного значения N будет выполнено условие  , где ε — заданная точность.

Вопрос 11

Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:

• Предел a или b (или оба предела) являются бесконечными;

• Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].

Несоб. Интеграл 1 рода: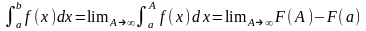

Если предел конечен, то интеграл сходится, иначе (илил несущ., бесконеч.) расходится

Несоб. Интеграл 2 рода: (?????????????????)

3 признака сходимости не соб. интегралов 1 рода от неотриц. ф-й.

1. 0≤f1(x)≤f2(x), x[a,∞)

Если сх. =>сх.

2) Если расх. =>расх.

3) 0≤φ₁(x), 0≤φ₂(x)

(≠0 ≠∞)

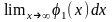, - одинаково

Приложения:

Существует и др. методы приближ. Вычисления интегралов. Например, подынт. ф-ю можно заменить многочленом Тейлора, получится квадратурная формула. Для получения оценки погрешности от замены интеграла квадратурной формулой, надо проинтегрировать остаток ф-лы Тейлора и ост. Оценить.

Вопрос 14

В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.

Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.

Рассмотрим функцию   от   аргументов в окрестности точки  . Для любого единичного вектора   определим производную функции   в точке   по направлению   следующим образом:

Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора  .

Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.

Связь с градиентом

Производную по направлению дифференциируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:

,

где   — орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора  .

Производные высших порядков

Если функция U = f  (x, y, z) имеет в некоторой (открытой) области x₀y₀ частную производную по одной из переменных, то названная производная, тоже являясь функцией от аргументов x, y, z, может, в свою очередь, в некоторой точке x₀, y₀, z₀ иметь частные производные по той же или по любой другой переменной. Для исходной функции U = f   (x, y, z) эти последние производные будут частными производными второго порядка. Если была взята первая производная по x ( ), то её вторые производные по x, y, z, будут записаны так:

Заметим, что частная производная высших порядков, взятая по разным переменным, называется смешанной производной.

Формула Тейлра (вопрос 6)