Вопрос 10

Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).

Пусть f(x) определена на [a, b]. Разобьём [a, b]на части с несколькими произвольными точками   Тогда говорят, что произведено разбиение R отрезка [a, b] Далее выберем произв. точку  , i=0,

Определённым интегралом от функции f(x) на отрезке [a, b] называется предел интегральных сумм при стремлении ранга разбиения к нулю  , если он существует независимо от разбиения R и выбора точек ξ_i, т.е.

Если существует указанный предел, то функция f(x) называется интегрируемой на 

[a, b] по Риману.

Задача приводящая к понятию определенный интеграл

Рассмотрим плоскую фигуру, ограниченную линиями y = 0, x = a, x = b и y = f(x), где f(x) есть непрерывная положительная функция, заданная при a ≤ x ≤ b (см. рис. 3). Такая фигура называется криволинейной трапецией. Поставим вопрос о площади F этой трапеции.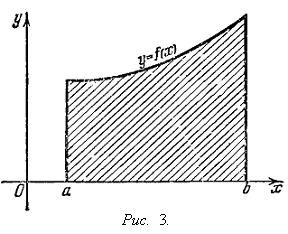

Разделим [a, b] точками a = x₀ < x₁ < x₂ < ... < x_n-1 < x_n = b и пусть λ = max(x_k+1 - x_k). Прямые x = x_k разбивают нашу трапецию на n узких полос. Так как функция f(x) непрерывна, то она мало меняется при x_k ≤ x ≤ x_k+1 и без большой погрешности ее можно считать на промежутке [x_k, x_k+1] постоянной и равной f(ξ_k), где ξ_k есть произвольно взятая точка промежутка [x_k, x_k+1]. Легко видеть, что сделанное допущение равносильно тому, что мы принимаем вышеупомянутые полосы за прямоугольники, а всю нашу трапецию - за ступенчатую фигуру, изображенную на рис. 4.

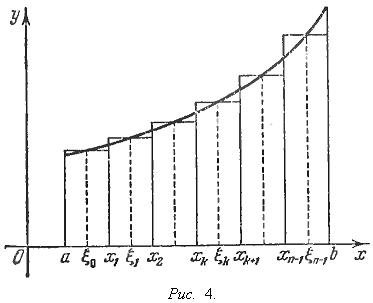Площадь этой ступенчатой фигуры, очевидно, равна Естественно считать, что эта площадь при малом λ является приближенным значением интересующей нас площади F. Поэтому по определению будем называть площадью нашей криволинейной трапеции предел

 

Если указанный предел существует и конечен и не завсит от способа деления отрезка, то этот предел и называется определенным интегралом

Свойства о. интегралов

1. a<b

2. ∫_a^a f(x) dx=0

3. Линейный функционал

4. 

5. 

6. 

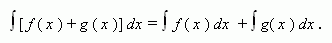
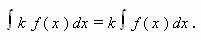
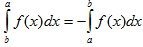
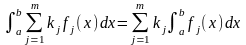
7. m≤f(x)≤M,

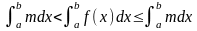
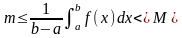
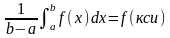
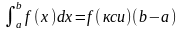
8. , x[a,b]

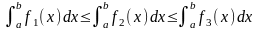
9. Аддитивность. Если y = f(x) интегрируема по отрезку [a,b] и точка c принадлежит этому отрезку, то 

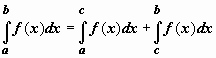
Формула Ньютона-Лейбница

Методы вычисления о. и.

Метод прямоугольников — метод численного интегрирования функции одной переменной, заключающийся в замене подынтегральной функции на многочлен нулевой степени, то есть константу, на каждом элементарном отрезке. Если рассмотреть график подынтегральной функции, то метод будет заключаться в приближённом вычислении площади под графиком суммированием площадей конечного числа прямоугольников, ширина которых будет определяться расстоянием между соответствующими соседними узлами интегрирования, а высота — значением подынтегральной функции в этих узлах. Алгебраический порядок точности равен 0.

Если отрезок [a,b]  является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по

Формуле левых прямоугольников: 

Формуле правых прямоугольников: 

Формуле прямоугольников (ср): 

Метод трапеций — метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подынтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями. Алгебраический порядок точности равен 1.

Если отрезок [a,b]  является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по формуле

Это простое применение формулы для площади трапеции — полусумма оснований, которыми в данном случае являются значения функции в крайних точках отрезка, на высоту (длину отрезка интегрирования). Погрешность аппроксимации можно оценить через максимум второй производной

Метод трапеций быстро сходится к точному значению интеграла для периодических функций, поскольку погрешность за период аннулируется. Метод может быть получен путём вычисления среднего арифметического между результатами применения формул правых и левых прямоугольников.

Формула Симпсона (также Ньютона-Симпсона) относится к приёмам численного интегрирования. Получила название в честь британского математика Томаса Симпсона.

Суть приёма заключается в приближении подынтегральной функции на отрезке [a,b] интерполяционным многочленом второй степени p₂(x), то есть приближение графика функции на отрезке параболой. Метод Симпсона имеет порядок погрешности 4 и алгебраический порядок точности 3. Формулой Симпсона называется интеграл от интерполяционного многочлена второй степени на отрезке [a, b] :

где f(a) , f((a+b)/2) и f(b) — значения функции в соответствующих точках (на концах отрезка и в его середине).